Pythonで線形代数!〜行列編(基礎・前編):数学×Pythonプログラミング入門(5/5 ページ)
AI・機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の各種計算や行、列の抽出、形状の変更方法などについて、プログラミングの方法を初歩から見ていく。
練習問題
では、練習問題に取り組みましょう。ここでは、要素ごとの演算の利用例として、共通鍵方式による画像の暗号化と復号の例を取り上げます(ただし、基本的な考え方のレベルにとどめます)。また、ブロードキャスト機能の利用例として、カラー画像をRGBにチャンネル分解する例を取り上げます。以下、問題の考え方について解説した動画も用意してあります。ぜひご視聴ください。
動画2 行列基礎・前編の練習問題
(1)共通鍵方式によって画像を暗号化/復号する
共通鍵方式では、暗号化と復号に同じ鍵を使います。そのための計算の基本は排他的論理和(XOR)です。排他的論理和を求めるには^演算子を使いますが、NumPyの配列では^演算子により、要素ごとの排他的論理和を求めることができます。
排他的論理和には面白い性質があり、A ^ B = Cのとき、C ^ B = Aとなります。そこで、Aを元のデータ、Bを共通鍵とすれば、A ^ Bを求めることにより、暗号化されたデータCが得られ、C ^ Bを求めることにより、元のデータAに復号できることになります。
従って、乱数を使って共通鍵Bを作り、送り手と受け手で同じ鍵を共有すれば暗号化通信ができます。もっとも、元のデータと暗号化されたデータの排他的論理和を取ると共通鍵が求められてしまう(A ^ C = Bとなる)ので、これだけでは安全ではないのですが、共通鍵方式の基本はこのような考え方です(あくまで基本の基本です)。詳細に興味のある方は『図解即戦力 暗号と認証のしくみと理論がこれ1冊でしっかりわかる教科書』(光成滋生著、技術評論社)などを参照してください。
というわけで、画像データとランダムな値の排他的論理和を取り、暗号化された画像データを作ってみましょう。ただし、その方法では、画像データと同じ長さの共通鍵が必要になり、あまりにも共通鍵が大きくなってしまいます。そこで、疑似乱数の種(seed)を共通鍵とすることにします。seedを固定すれば同じ疑似乱数が作れるので、seedを送り手と受け手で共有すれば、それを基に同じ疑似乱数が作成でき、暗号化と復号ができます。
画像を以下のリスト14のコードで読み込み、暗号化と復号を行うコードを書いてみてください(関数にしなくても構いません)。
from imageio import imread
import matplotlib.pyplot as plt
url = 'https://github.com/Gessys/math/blob/main/data/bird.png?raw=true'
image = imread(url) # imageに読み込む
plt.imshow(image) # 表示してみる
plt.show()
GitHub上に置いてあるbird.pngという画像ファイルを読み込んで表示する。読み込まれた画像データはimageという変数で参照される。
このコードで読み込まれる画像データは行位置/列位置/色深度を表す3つの軸を持つ三次元の配列です。色深度は[R, G, B, α]で表され、いずれも0〜255の符号なし8ビット整数(np.uint8)です。「色深度」という言葉は聞き慣れないかもしれませんが、「行」と「列」に対し「奥行き」に例えることができるので、そう呼ばれます。
(ヒント)以下の手順で進めます。
- 疑似乱数のseedを255とする(これを共通鍵とします)
- 符号なし8ビット整数の疑似乱数を画像データと同じサイズだけ作成する
- NumPyの配列では、サイズ(全ての要素の個数)を求めるためにsize属性が使える
- 疑似乱数はnp.random.randint関数を使って作る。引数には乱数の下限と上限、size引数に作成する乱数の個数、dtype引数に作成する乱数のデータ型(np.uint8)を指定する
- 作成した疑似乱数を画像と同じ形にreshapeする(その配列をmaskという名前にします)
- 画像データの配列の形を得るにはshape属性が使えるので、それをreshapeメソッドに指定する
- 画像データとmaskの排他的論理和を取り、暗号化された画像データを作成し、表示する
- 暗号化された画像とmaskの排他的論理和を求め、元の画像データに戻し、表示する
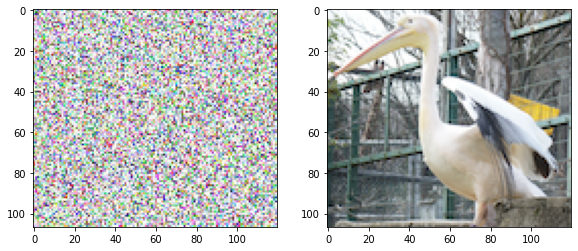
結果は図5のようになります。
(2)カラー画像をRGBにチャンネル分解する
続いて、カラー画像から、R(赤)、B(青)、G(緑)の各成分を取り出すためのコードを書いてみましょう。色の表し方にはいくつかの方法があるのですが、練習問題(1)の画像と同じ形式であるものとします。まず、前提知識として、リスト15に示す簡単なカラー画像(image)の例を使って色の取り扱い方を確認しておきましょう。
import numpy as np
import matplotlib.pyplot as plt
image = np.array([[[233, 55, 36, 255], [231, 50, 245, 255], [168, 245, 253, 255]],
[[104, 223, 181, 255], [247, 236, 80, 255], [247, 203, 248, 255]]])
plt.imshow(image) # 表示してみる
plt.show()
print(image[0, 1])
# 出力例:
# [231 50 245 255]
簡単なカラー画像で色の取り扱い方を確認しておこう。0行1列目の色は[231 20 245 255]となっている。次に示す図6が実際の画像。

図6 簡単なカラー画像の例
0行1列目の色(マゼンタに近い色)は、リスト15で見たように[231, 20, 245, 255]となっている。これらの値はR(赤)、B(青)、G(緑)、α(不透明度)の順になっている。
この画像データでは、最初の軸が行位置、次の軸が列位置、最後の軸が色深度を表しています。例えば、0行1列目の色深度、つまり、image[0, 1]の値は[231, 50, 245, 255]となっています。これらの値は、順に、R(赤)、G(緑)、B(青)、α(不透明度)を表しています。従って、この例なら赤の強さが231、緑の強さが50、青の強さが245、不透明度が255となります。
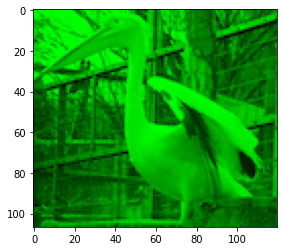
色の表し方が分かったので、画像データをRGBにチャンネル分解してみましょう。例えば、赤のチャンネルを取り出すには、Rとαの値を変えずにGとBの値を0にします。
このようにしてチャンネル分解された画像データを返す関数decompを作成してみてください。引数には元の画像データを表す配列と、取り出すチャンネルを表すベクトルを指定します。例えば、緑を取り出すのであれば、[0, 1, 0, 1]のように、緑の位置を1としたベクトルにします。不透明度は常にそのまま取り出すので、最後の要素は必ず1とします。
実行例は以下のとおりです。リスト16のように関数decompを呼び出して得られたデータを画像として表示すると、図6のようになります。imageは練習問題(1)で読み込んだものです(もちろんリスト15のimageを指定しても動作します)。なお、関数decompの内容はたったの1行で書けます!
mask = [0, 1, 0, 1] # Gとαを取り出す
gch = decomp(image, mask)
plt.imshow(gch)
plt.show()
maskには、[R, G, B, α]の形のベクトルを指定するものとし、1ならばそのチャンネルの値を取り出す、0ならば取り出さない(その色は0とする)ことを表す。αについては、常に1としておく。
練習問題の解答例
以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。
(1)共通鍵方式によって画像を暗号化・復号するコード
以下のようになります。コード中のコメントを追いかければ、何をしているのかが分かると思います。
from imageio import imread
import numpy as np
import matplotlib.pyplot as plt
url = 'https://github.com/Gessys/math/blob/main/data/bird.png?raw=true'
image = imread(url)
# 送信側
np.random.seed(255) # 共通鍵の指定。乱数のseedである255が共通鍵
# 疑似乱数の作成(画像データと同じ個数)
r = np.random.randint(0, 256, size=image.size, dtype=np.uint8)
mask = r.reshape(image.shape) # 作成された乱数をイメージと同じ形の配列にする
encrypted = image ^ mask # 排他的論理和を求め、暗号化する
plt.imshow(encrypted) # 暗号化された画像を表示する
plt.show()
# 受信側
np.random.seed(255) # 共通鍵の指定。乱数のseedである255が共通鍵
# 疑似乱数の作成(暗号化されたデータと同じ個数)
r = np.random.randint(0, 256, size=encrypted.size, dtype=np.uint8)
mask = r.reshape(image.shape) # 作成された乱数をイメージと同じ形の配列にする
decrypted = encrypted ^ mask # 排他的論理和を求め、復号する
plt.imshow(decrypted) # 復号された画像を表示する
plt.show()
同じ形の配列同士で、個々の要素ごとに一括して排他的論理和を求めている。繰り返し処理を一切書かなくても全ての要素の処理ができる。
実際には、これだけでは脆弱すぎて使い物にはなりませんが、共通鍵方式による暗号化と復号の基本の基本については理解できると思います。
(2)カラー画像をRGBにチャンネル分解するコード
以下の通りです。関数の中身はホントにたったの1行ですね。
def decomp(image, mask):
return image * mask
ブロードキャスト機能により、全ての色深度にmaskの値が掛けられるので、maskが1となっている色は元の値となり、maskが0となっている色は0になった配列が返される。
なお、np.asarray((image * mag).clip(max=255), dtype=np.uint8)といったコードを書けば、画像の明るさをmag倍にした配列が得られます。clipメソッドは、最小値や最大値を超えないようにするためのメソッドです。色や不透明度を表す値は0〜255なので、その範囲に収まるようにしたわけです。また、小数点以下のある数値を掛けると、結果が浮動小数点数になるので、この場合は、asarray関数を使って符号なし8ビット整数に変換する必要があります。
というわけで、今回はここまでとしましょう。前回に引き続き、AI/機械学習に必要とされる線形代数の知識やプログラミングの方法について、行列の考え方や基本的な計算方法、NumPyによる配列の取り扱いなどを見てきました。
次回は、内積を中心としたお話をします。さらに、応用編では、行列式や固有値や固有ベクトルなど、線形代数ならではの考え方や、それを応用してデータの分析などに活用する方法を見ていくこととします。
Copyright© Digital Advantage Corp. All Rights Reserved.