Pythonで線形代数！〜行列編（基礎・後編）：数学×Pythonプログラミング入門（3/4 ページ）

AI／機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の内積の計算方法とその応用について、プログラミングの方法を初歩から見ていく。

[羽山博，著]

目標3： 三次元以上の配列での@演算子とdot関数の違いを確認する

　三次元以上の配列では、@演算子、dot関数、inner関数は全て働きが異なります。これについても具体例を挙げてみてください……と言いたいところですが、配列の軸のサイズによっては計算ができない場合があり、うまく計算できる例を探すのは難しいかもしれません。そこで、以下のような三次元配列を作ってどのような計算が行われているのかを確認することを目標としましょう。ただし、ここからはかなり細かな話になるので、面倒だなと思うようであればスルーして、最後の練習問題に取り組んでもらっても構いません。

• 0以上12未満の等差数列をNumPyの一次元配列として作る
• それを2×3×2の三次元配列に変形し、Aという名前で参照できるようにする
• 同様に、2×2×3の三次元配列に変形し、Bという名前で参照できるようにする
• AとBについて、@演算子とdot関数を適用した結果を求め、違いを確認する

　ちょっとしたヒントです。等差数列を作るにはNumPyのarange関数が使えます。また、配列の形を変えるためにはreshapeメソッドを利用します（いずれも既に登場しています）。

　ただし、上の形の配列ではinner関数による内積は求められません。inner関数については、配列Aと、配列Bを転置した配列の内積を求めてみてください。

3. 三次元以上の配列で@演算子、dot関数、inner関数の違いを確認するためのコードを書く

　目標に示した手順通りにやってみましょう。まず、配列A、配列B、配列Bを転置したものがどうなっているかを見ておきます（リスト5）。

import numpy as np

A = np.arange(12).reshape((2, 3, 2))
B = np.arange(12).reshape((2, 2, 3))

print("配列A：" , A.shape)
print(A)
# 出力例
# 配列A：(2, 3, 2)
# [[[ 0  1]
#   [ 2  3]
#   [ 4  5]]
#
#  [[ 6  7]
#   [ 8  9]
#   [10 11]]]

print("配列B：" , B.shape)
print(B)
# 配列B：(2, 2, 3)
# [[[ 0  1  2]
#   [ 3  4  5]]
#
#  [[ 6  7  8]
#   [ 9 10 11]]]

print("配列B.T：" , B.T.shape)
print(B.T)
# 配列B.T：(3, 2, 2)  # (2, 2, 3)が(3, 2, 2)のように逆順になっている
# [[[ 0  6]
#   [ 3  9]]
#
#  [[ 1  7]
#   [ 4 10]]
#
#  [[ 2  8]
#   [ 5 11]]]

リスト5　多次元配列を作る
多次元配列は行や列だけでは表しにくいが、例えて言うなら、配列Aは2枚のワークシートに3行2列のセルがあるExcelの表のようなものと考えられる。配列Bは2枚のワークシートに2行3列のセルがある表となる。配列Bと配列B.Tの関係をワークシートの例えで表そうとするとかえって難しくなってしまうが、単に、(i, j, k)という軸が(k, j, i)の順になったと考えればよい。shape属性を指定して配列の形も表示しておいた。

　では、それぞれの内積を求めてみましょう。リスト5の続きに、以下のリスト6のコードを入力して実行してみてください。

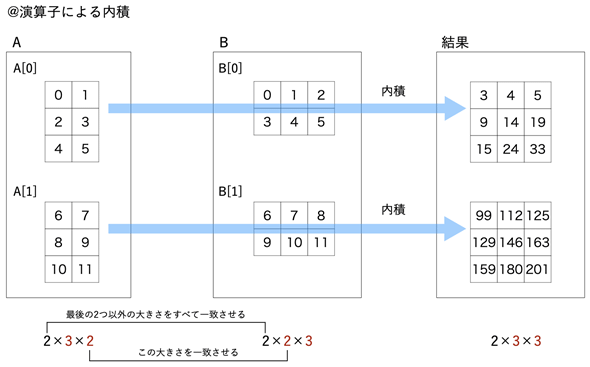
print("@演算子による内積：", (A @ B).shape) # リスト5の続き
print(A @ B)
# 出力例
# @演算子による内積： (2, 3, 3)
# [[[  3   4   5]
#   [  9  14  19]
#   [ 15  24  33]]
#
#  [[ 99 112 125]
#   [129 146 163]
#   [159 180 201]]]

print("dot関数による内積：" , np.dot(A, B).shape)
print(np.dot(A, B))
# dot関数による内積： (2, 3, 2, 3)
# [[[[  3   4   5]
#    [  9  10  11]]
#
#   [[  9  14  19]
#    [ 39  44  49]]
#
#   [[ 15  24  33]
#    [ 69  78  87]]]
#
#
#  [[[ 21  34  47]
#    [ 99 112 125]]
#
#   [[ 27  44  61]
#    [129 146 163]]
#
#   [[ 33  54  75]
#    [159 180 201]]]]

print("inner関数による内積：" , np.inner(A, B.T).shape)
print(np.inner(A, B.T))
# inner関数による内積： (2, 3, 3, 2)
# [[[[  6   9]
#    [  7  10]
#    [  8  11]]
#
#   [[ 18  33]
#    [ 23  38]
#    [ 28  43]]
#
#   [[ 30  57]
#    [ 39  66]
#    [ 48  75]]]
#
#
#  [[[ 42  81]
#    [ 55  94]
#    [ 68 107]]
#
#   [[ 54 105]
#    [ 71 122]
#    [ 88 139]]
#
#   [[ 66 129]
#    [ 87 150]
#    [108 171]]]]

リスト6　@演算子とdot関数による内積の結果の違い
@演算子を使った場合は結果が2×3×3の配列になり、dot関数の場合は結果が2×3×2×3の配列になっている。inner関数の場合は結果が2×3×3×2の配列になっている。どのように計算が行われているかについては後述する。

　三次元以上になると計算のルールがかなり複雑になるので、どのように計算されているか、図解で丁寧に追いかけていくことにします。これについては動画でも解説しているのでぜひご視聴ください。

動画2　三次元以上の配列での@演算子／dot関数／inner関数の計算ルール

　@演算子による計算では、A[0]とB[0]の内積、A[1]とB[1]の内積がそれぞれ求められ、配列として返されます（図4）。

図4　@演算子による内積の計算方法
@演算子による計算方法は比較的分かりやすい。最後の2つの軸の内積が求められ、配列として返されると考えればよい。

　一方、dot関数による計算では、A[0]とB[0]の内積、A[0]とB[1]の内積、A[1]とB[0]の内積、A[1]とB[1]の内積が図5のように計算され、配列として返されます。

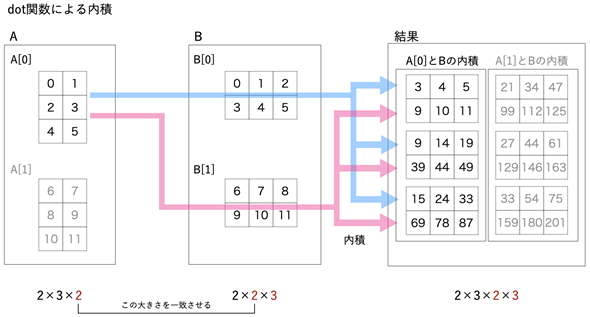
図5　dot関数による内積の計算方法
A[0]とB[0]の内積がブルーの線のように配置され、A[0]とB[1]の内積がピンクの線のように配置される。A[1]とB[0]の内積、A[1]とB[1]の内積については矢印で示していないが、同じように考えればよい。

　inner関数による計算は、dot関数と似ていますが、内積を計算するときに、目標2で見たような行同士の積和を求めていることが分かります（図6）。

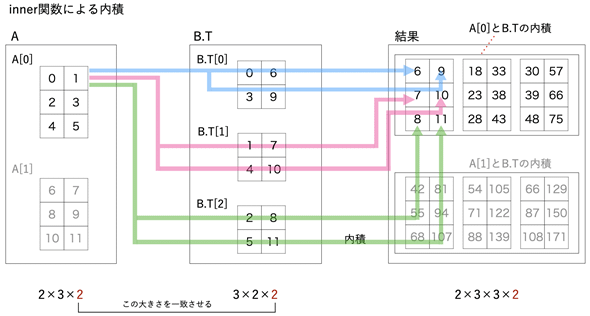
図6　inner関数による内積の計算方法
A[0]とB.T[0]の内積がブルーの線のように配置され、A[0]とB.T[1]の内積がピンクの線のように配置され、A[0]とB.T[2]の内積が緑の線のように配置される。行同士の積和を求めていることに注意。A[1]とB.T[0]の内積、A[1]とB.T[1]の内積、A[1]とB.T[2]の内積については矢印で示していないが、同じように考えればよい。

　三次元以上の配列の積を求める場合には、配列の形を合わせるのに悩みますね。@演算子では、最後の2つ以外の軸のサイズを合わせ、最後の2つの軸をn×kとk×mの形にしておきます。以下の例（リスト7、図7）は配列の形と内積の計算を行った結果の形を確認するためのコードです。形が分かればいいので、作成する配列は全ての要素が1の単純なものとします。

import numpy as np

A = np.ones((2, 4, 5, 3)) # 2×4×5×3の形で、全ての要素が1の配列
B = np.ones((2, 4, 3, 6)) # 2×4×3×6の形で、全ての要素が1の配列
C = np.ones((2, 3, 3, 6)) # 2×3×3×6の形で、全ての要素が1の配列

print((A @ B).shape)
print((A @ C).shape)
# 図7が出力例

リスト7　@演算子が適用できる配列の形
NumPyのones関数により、全ての要素が1の配列を作る。引数には配列の形をタプルやリストで指定する。shape属性を指定すれば、配列の形が得られるので、それを利用しA@Bの結果ではなく、形だけを表示した。

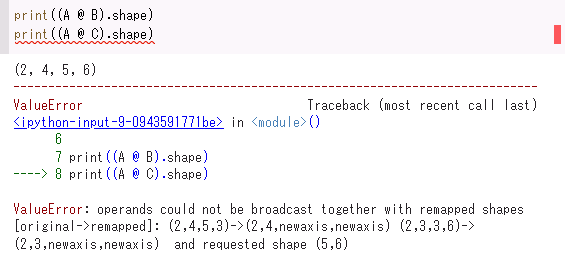
図7　@演算子による三次元配列の内積を計算できない場合のエラー出力例
A@B（AとBの内積）の結果は2×4×5×6の配列となったことが分かる。
A@Cは最後の2つ以外の軸（ここでは2つ目の軸）のサイズが異なるのでエラーとなる。

　@演算子を適用した場合、配列の形が(a₁, a₂, ..., n, k)と(a₁, a₂, ..., k, m)であれば、返される配列の形は(a₁, a₂, ..., n, m)となります。np.onesの引数の値をいろいろと変えて試してみるといいでしょう。ただし、一方の配列の最初の軸のサイズ（a₁の値）が1である場合は、他方の最初の軸のサイズが異なっても正しく動作します（ブロードキャスト機能によるものです）。

　dot関数では、最後の2つの軸がn×kとk×mの形であれば計算ができます（リスト8）。

import numpy as np

A = np.ones((2, 4, 5, 3)) 
B = np.ones((2, 4, 3, 6))
C = np.ones((2, 3, 3, 6))

print(np.dot(A, B).shape)  # 最後がn×k, k×mとなっている
print(np.dot(A, C).shape)
# 出力例：
# (2, 4, 5, 2, 4, 6)
# (2, 4, 5, 2, 3, 6)

リスト8　dot関数が適用できる配列の形
dot関数の場合は配列の最後の軸のサイズがn×kとk×mになっていれば計算ができる。

　dot関数を適用した場合、配列の形が(a₁, a₂, ..., n, k)と(b₁, b₂, ..., k, m)であれば、返される配列の形は(a₁, a₁, ..., n, b₁, b₂, ..., m)となります。

　inner関数では、最後の軸が同じサイズであれば計算ができます（リスト9）。

import numpy as np

A = np.ones((2, 4, 5, 3)) 
B = np.ones((2, 4, 3, 6))
C = np.ones((2, 3, 3, 6))

print(np.inner(B, C).shape)
print(np.inner(A, C).shape)
# 図8が出力例

リスト9　inner関数が適用できる配列の形

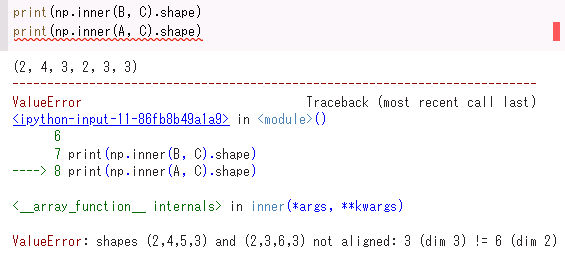
図8　inner関数による三次元配列の内積を計算できない場合のエラー出力例
inner(B, C)は最後の軸が同じサイズなので計算できる。
しかし、inner(A, C)は最後の軸のサイズが異なるのでエラーとなる。

　inner関数を適用した場合、配列の形が(a₁, a₂, ... n ,k)と(b₁, b₂, ... m, k)であれば、返される配列の形は(a₁, a₂, ..., n, b₁, b₂, ... , m)となります。

　今回は、NumPyでの内積の計算方法について、かなり細かく見てきました。その分、実際の事例に則した内積の利用例が少なくなったので、どう使うのかイメージが湧かないという方もおられるかもしれません。そこで、以下の練習問題では、ちょっとした利用例を取り上げてみました。内積についての理解を確実にするとともに、どのような応用ができるかぜひ思い描いてみてください。