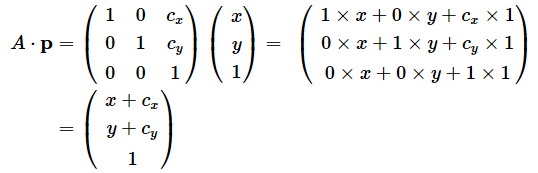Pythonで線形代数！〜行列編（基礎・後編）：数学×Pythonプログラミング入門（4/4 ページ）

AI／機械学習で使われるデータを表現するためにはベクトルや行列などの線形代数を理解することが必要不可欠。今回は行列の内積の計算方法とその応用について、プログラミングの方法を初歩から見ていく。

[羽山博，著]

練習問題

　では、練習問題に取り組みましょう。内積がどのように利用されるかが分かるように、問題の考え方について解説した動画も用意してあります。ぜひご視聴ください。

動画3　行列基礎・後編の練習問題

（1）ニューラルネットワークの入力値を求める

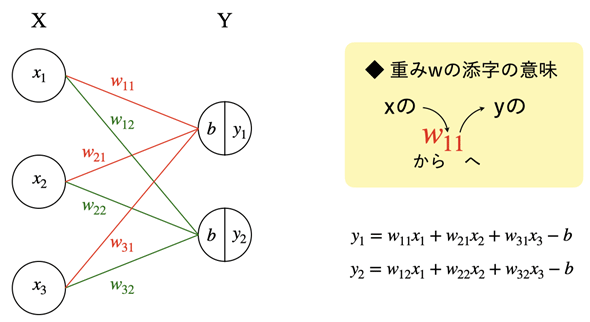
　図9のようなニューラルネットワークがあるとき、X層の出力を基に、Y層に入力される値を求めてみましょう。入力される値はXの出力に重みWを掛け、バイアスbを引いたものとします。

図9　簡単なニューラルネットワーク
Y層への入力値は図中に示した式で求められる（Y層からの出力値はこれらに評価関数を適用したものとなるが、ここでは入力値のみを求めることとする）。

　このようなニューラルネットワークは行列とベクトルの積を使って表せます。そのためのコードを書き、Y層への入力値を求めてみてください。以下のような出力例が得られると正解です。1行でできるので、穴埋めで答えてみてください。

import numpy as np

X = np.array([1, 1, 0])
W = np.array([[0.5, -0.4],
              [0.3, 0.2],
              [0.8, -0.1]])
b = 0.5

print(　　　ア　　　)
# 出力例：
# [ 0.3 -0.7]

リスト10　ニューラルネットワークで重みを付けた入力値を得る（問題）
図9の添え字に従って、Xをベクトルとして表し、重みを配列Wとして表した。実行結果が[ 0.3 -0.7]になれば正解。

（ヒント）WとXの内積を求めてbを引けば、Y層への入力値が求められます。内積を求める場合はWの形に注意が必要です。

（2）指定した点を中心にベクトルを回転させる

　3×3行列を使ってベクトルを平行移動させる関数moveと、ベクトルを反時計回りに角度θだけ回転させる関数rotateを作成し、任意の点(c_x, c_y)を中心として、任意のベクトルp＝(x, y)を角度θだけ反時計回りに回転させるコードを書いてみてください。

　これらの関数を使って、点(2,1)を中心として、ベクトルp＝(4,5)を30度（π/6ラジアン）回転させた座標を求めると[1.73205081 5.46410162 1.]という結果が得られます。

（ヒント）p＝(x, y)を(c_x, c_y)だけ平行移動させるには、以下のような行列Aを用意し、pとの内積を求めます。ただし、pを(x, y, 1)と表しておきます。

　c_xがX方向への移動量、c_yがY方向への移動量です。内積を計算すると、

となり、確かに平行移動できていることが分かります。なお、行列やベクトルの3行目は、計算を一度に行うために付加したものにすぎません。pの座標はそれを除いた(x, y)で、平行移動した後の座標は(x＋c_x, y＋c_y)です。

　原点を中心に反時計回りに回転を行うための行列も、同様に、

と表すことができます。内積の計算方法を理解するための簡単な練習問題では、回転を行うための行列を2×2行列としましたが、上のような3×3行列を利用すれば、平行移動や回転その他さまざまな変形ができるようになります。

（さらなるヒント）原点ではなく、点(c_x, c_y)を中心に点pを回転させるには、点(c_x, c_y)が原点になるように座標を移動します。その場合、点pは(−c_x, −c_y)だけ平行移動します。その点を回転させた後、また原点を元に戻すために座標を(c_x, c_y)だけ移動すればうまくいきます。

練習問題の解答例

　以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。

（1）ニューラルネットワークの入力値を求める

　以下の通りです。

import numpy as np

X = np.array([1, 1, 0])
W = np.array([[0.5, -0.4],
              [0.3, 0.2],
              [0.8, -0.1]])
b = 0.5

print(W.T @ X  - b)
# 出力例：
# [ 0.3 -0.7]

リスト11　ニューラルネットワークで重みを付けた入力値を得る（作成例）
Wは3行2列の配列、Xは3列のベクトルと考えられるので、Wを転置し、2行3列とすればよい。

（2）指定した点を中心にベクトルを回転させる

　一次変換のための行列を作成する関数は、単にNumPyの配列を作って返すだけです。点(2,1)を中心に点p＝(4, 5)を30度回転させるには、p＝(4, 5)を(−2, −1)だけ平行移動させ、次に30度（π/6ラジアン）回転させ、また(2, 1)だけ平行移動します。それぞれの配列をベクトルに左から掛けていけば答えが求められます。

def move(Dx, Dy):
  return np.array([[1, 0, Dx],
                   [0, 1, Dy],
                   [0, 0, 1]])

def rotate(theta):
  return np.array([[np.cos(theta), -np.sin(theta), 0],
                   [np.sin(theta), np.cos(theta), 0],
                   [0, 0, 1]])

p = np.array([4, 5, 1])

print(move(2, 1) @ rotate(np.pi/6) @ move(-2, -1) @ p)
# 出力例：
# [1.73205081 5.46410162 1.        ]

リスト12　点(2, 1)を中心に、点(4, 5)を30度回転させた座標を求める
拡大や縮小など、一次変換を行う関数を作っておき、それらを組み合わせればさまざまな拡大／縮小や変形ができることが分かる。変換を行う配列はベクトルの左から掛けていくことに注意。

　内積の計算は結合法則が成り立つので、あらかじめ行列の内積を求めておき、それを左からベクトルに掛けても構いません。結局のところ、(c_x, c_y)を中心として、点p＝(x, y)をθラジアン回転させた後の座標は、

という計算だけで求められるのですが、リスト12のような基本的な変形を行うための行列を用意しておき、それらの内積を求めていくと、どのような変形を行っているのかが分かりやすいですね。今回は1つの点を動かしただけですが、画像の全ての点の座標についてこのような操作をすれば、画像の平行移動や回転などの変形ができます。

---

　今回はここまでです。前回に引き続き、AI／機械学習に必要とされる線形代数の知識やプログラミングの方法について、行列の考え方や基本的な計算方法、NumPyによる配列の取り扱いなどを見てきました。

　次回は、行列式や固有値や固有ベクトルなどの線形代数ならではの考え方や、それらをデータの分析などに活用する方法を見ていくこととします。

「数学×Pythonプログラミング入門」