Pythonで三角関数！～サウンドも作成してみよう：数学×Pythonプログラミング入門（1/4 ページ）

三角関数の基本を確認し、Pythonでプログラミングしてみよう。練習問題では、三角関数を使ってサウンドを作成したり、サウンドデータを読み込んで波形を表示したりするための初歩的なプログラムを作成する。また、サウンドを分析するために使われる離散フーリエ変換の利用についても発展的な話題として簡単に触れる。

[羽山博，著] PC用表示関連情報

LINE

Hatena

連載目次

　前回は線形代数の難所である行列式と固有値／固有ベクトルを求める方法と応用例を見ました。今回は三角関数の基本として、弧度法による角度の表し方や余弦（cos）と正弦（sin）の意味を確認した後、練習問題を通して、三角関数によるサウンドの作成方法やサウンドデータの読み込みと可視化の方法を見ていきます。窓関数（ハニング窓）の利用や、離散フーリエ変換を利用してサウンドを分析するコードの例についても最後に紹介します。

連載：

『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』

この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI／機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。

羽山博

筆者紹介： IT系ライター、大学教員（非常勤）。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得するもバイクの購入資金が全くない。

目標1：弧度法による角度の表し方を確認する

　私たちが小学校の算数で学んだ角度の表し方では、原点の周りを一周した場合の角度が360度となっています。直角は90度ですね。このような角度の表し方を度数法と呼びます。高校の数学では三角関数を学びますが、三角関数では弧度法と呼ばれる角度の表し方を一般的に使います。弧度法では、原点の周りを一周した場合の角度が2πラジアンとなります。

　そこで、度数法で表された角度を弧度法で表された角度に変換してみましょう。実際のところ、mathモジュールやnumpyモジュールのradians関数を使えば、弧度法の考え方が分からなくても換算はできるのですが、ここでは、換算を行うための式を自分で立てて計算してみましょう。これが今回の目標1です（関数を作る必要はありません）。

　例えば、度数法の90度は弧度法では、

となります。60度なら、

です。なお、円周率πの値としてはmathモジュールの定数piやnumpyモジュールの定数piを使って構いません。

1. 弧度法による角度の表し方を確認するためのコードを書く

　度数法の角度（度単位）を弧度法の角度（ラジアン単位）に換算する方法は、

を掛けるだけなので、計算方法さえ知っていればできてしまいます。また、上で述べたようにradians関数を使えば計算方法を知らなくても換算できます。そのため、弧度法の理解があやふやなままになっている人もいるかもしれません。

　まず換算を行うコード（リスト1）を見てから、後で弧度法の考え方を確認することにしましょう。

import numpy as np

deg = float(input("度単位で角度を入力してください："))
# 入力例：
# 度単位で角度を入力してください：90 # 90と入力する

print("換算結果は:", deg * np.pi / 180, "ラジアン")
print("radians関数による検算:", np.radians(deg), "ラジアン")
# 出力例：
# 換算結果は: 1.5707963267948966 ラジアン
# radians関数による検算: 1.5707963267948966 ラジアン

リスト1　角度を度単位からラジアン単位に変換する
input関数はキーボードから文字列を入力するための関数。float関数を使って、入力された文字列が数値と見なせる場合は浮動小数点数に変換する。度数法の360度が2πに当たるので、2π/360＝π/180を掛ければ、ラジアン単位に変換できる。

　では、弧度法の考え方をおさらいしておきましょう。一周を2πとする、ということですが、そもそも「一周」というのは何でしょうか。もう少しきちんと定義しておきましょう。以下のお話については、動画でも解説しているので、ぜひご視聴ください。

動画1　ラジアンの正体

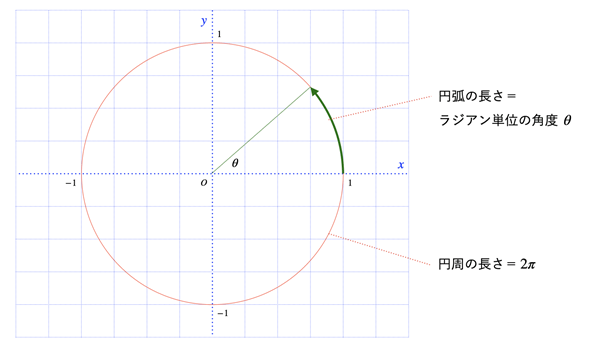
　まず、半径r＝1の円を考えます。半径1の円は単位円と呼ばれます。r＝1なので、円周の長さは2π r＝2πですね。これを「一周」の角度と考えます。つまり、図1に示したように、単位円の円周（や円弧）の長さをそのまま角度に対応させるというわけです。

図1　弧度法では単位円の円弧の長さを角度とする
単位円の円弧の長さをそのまま角度とするので、弧度法と呼ばれる。反時計回りの角度が正、時計回りの角度が負となる。

　このことから、円周の半分なら弧度法での角度は、

となることが分かります（度数法では180度に当たります）。また、直角は円周の1/4なので、弧度法での角度は、

となります*1。

*1　半径が1でない場合は円弧の長さが変わるじゃないですか、と言われるかもしれません。ごもっともです。が、半径と円弧の長さの比を弧度法の角度とするので、半径が変わっても角度は同じです。例えば、半径がrのとき、円周の長さは2π rなので、その比は2π r/r ＝ 2πです。分子にも分母にもrが現れるので、約分すればrが消えます。r＝1としたのは計算を簡単にするためです。

　理屈が分かったところで、換算の方法もあらためて確認しておきましょう。度数法の360度が2πに当たるので、deg度がradラジアンに当たるものとすれば、