Pythonで統計・データ分析！〜基本統計量の活用と機械学習の基本：数学×Pythonプログラミング入門（2/5 ページ）

データ分析において最もよく使われる表形式のデータを取り扱う方法を見ていく。まず、pandasデータフレームの基本的な取り扱い方法を確認し、次に、各種の基本統計量を求める。また、基本統計量の可視化を行い、データの「見方」についても触れる。最後に、scikit-learnを使った回帰と分類の簡単な例を紹介する。

[羽山博，著]

目標2： 基本統計量と相関行列を求める

　データフレームにデータを読み込むことができれば、基本統計量や相関行列を求めるのは簡単です。目標1で見たカリフォルニアの住宅価格データを使って以下のような統計量を求めてみましょう。

• 基本統計量（データの個数、平均値、標準偏差、四分位数など）を求める
• 相関行列を求める

　基本統計量はデータフレームのdescribeメソッドを使えば求められます。また、相関行列もデータフレームのcorrメソッドを使えば求められます。コードを書いて実行するだけでなく、得られた結果についても考察してみてください。

2. 基本統計量と相関行列を求めるためのコード

　データフレームのdescribeメソッドは、データの個数や平均値、標準偏差、四分位数などの基本統計量を全て返してくれます。住宅価格データを読み込んで、基本統計量を表示しましょう（リスト15、図9）。

import pandas as pd

df = pd.read_csv('./sample_data/california_housing_train.csv')
df.describe()

リスト15　カリフォルニアの住宅価格データを読み込んで基本統計量を求めるコード
データフレームのdescribeメソッドを呼び出すだけで、基本統計量が全て求められる。

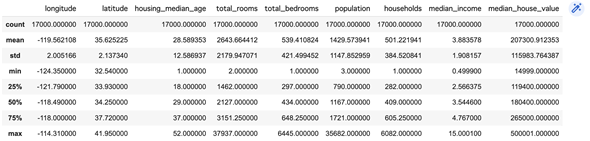
図9　リスト15の実行結果（住宅価格データの基本統計量）
各行の値は、先頭から順に、データの件数（count）、平均値（mean）、標準偏差（std）、最小値（min）、第1四分位数（25%）、中央値（50%）、第3四分位数（75%）、最大値（max）となっている。

　基本統計量の値を見ただけでは、データの特徴はあまり分からないかもしれませんが、データの件数（count）と最小値（min）、最大値（max）をざっと見ておきましょう。標本のサイズや値の範囲が分かります*2。第1四分位数はデータ全体を小さいものから順に並べたときに、先頭から1/4つまり25％の位置にある値のことです。第3四分位数なら3/4つまり75％の位置にある値となります。

*2　件数の異なる列がある場合、欠損値が存在します。ただし、全ての列の件数が同じであっても、欠損値が存在しないとは言い切れないことに注意してください。全ての列に同じ数の欠損値があるかもしれないからです。df.isnull().sum()とすれば、各列の欠損値の個数が求められます。

　また、平均値（mean）と中央値（50％）も比較しておくと分布の特徴がある程度分かります。中央値はデータ全体を小さいものから順に並べたときにちょうど真ん中にある値のことですね。

• 平均値＞中央値であれば、左に山のある分布（小さい値が多く、大きい値が少ない）
• 平均値＜中央値であれば、右に山のある分布（大きい値が多く、小さい値が少ない）

となっています。平均値と中央値がほぼ等しい場合は中心に山のある正規分布……と言いたいところですが、必ずしもそうとは限りません。一様分布でも平均値と中央値はほぼ等しくなりますし、左と右の両方に山がある分布でも平均値と中央値がほぼ等しくなることがあります。従って、数値だけを見て結論に飛びつくのではなく、ヒストグラムや散布図などを作成して全体像を確認しておく必要があります。が、それは次の目標にすることとして、先に相関行列を求めておきましょう。

　相関行列は、データフレームのcorrメソッドで求められます（リスト16、図10）。

# リスト15の続きに入力する
df.corr()

リスト16　カリフォルニアの住宅価格データの相関行列を求めるコード

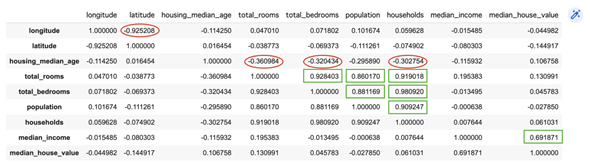
図10　リスト16の実行結果（住宅価格データの相関行列）
相関行列を作成すれば、全ての項目同士の相関係数が求められる。対角成分は自分自身との相関係数なので1になる。この図では、正の相関が0.3以上の項目を緑の四角で囲んでおいた。例えば、部屋数（total_rooms）と寝室数（total_bedrooms）の0.928403など。また、負の相関が-0.3以下の項目は赤の楕円で囲んである。例えば、築年数（housing_median_age）と部屋数（total_rooms）の-0.360984など。いずれも、対角成分を挟んで対称の位置にある値は同じなので、右上の値にだけ印を付けてある。

　相関行列を見れば、それぞれの項目の関係がある程度分かります。相関係数が1に近い正の値の場合は、一方の項目の値が大きくなれば、他方の項目の値も大きくなるということです。逆に、-1に近い負の値の場合は、一方の項目の値が大きくなれば、他方の項目の値は小さくなるということです。

　例えば、経度（longtitude）と緯度（latitude）に高い負の相関が見られますが、これはカリフォルニア州が左上から右下に位置する「＼」のような形になっているからです。経度が小さくなれば（西＝左に行くと）、緯度は大きくなります（北＝上に行く）。部屋数と寝室数に正の相関があるのは当然ですね。世帯収入と住宅価格に正の相関があるのもうなずけます。寝室数と住宅価格の相関係数は0に近いので、これらにはあまり関係がなさそうです（超豪邸はある程度大きな住宅でも、多くの場合、寝室数は1つです）。

　すでに述べたように、数字を見ただけでは分かりにくいデータの特徴もあります。そこで、次の目標3ではデータの可視化を行いましょう。