Pythonで統計・データ分析！〜基本統計量の活用と機械学習の基本：数学×Pythonプログラミング入門（3/5 ページ）

データ分析において最もよく使われる表形式のデータを取り扱う方法を見ていく。まず、pandasデータフレームの基本的な取り扱い方法を確認し、次に、各種の基本統計量を求める。また、基本統計量の可視化を行い、データの「見方」についても触れる。最後に、scikit-learnを使った回帰と分類の簡単な例を紹介する。

[羽山博，著]

目標3： 分布や関係を可視化する

　目標3はデータの特徴を可視化することです。データの分布や項目同士の関係を可視化するために、以下のようなグラフを描いてみましょう。

• 築年数と、世帯年収の箱ひげ図
• 世帯年収のヒストグラム
• 全ての変数同士の散布図

　箱ひげ図はデータの範囲や外れ値を見るため、ヒストグラムは度数の分布を見るため、散布図は関係を見るために使われます。

3. 分布や関係を可視化するためのコード

　グラフを描く方法については、すでにこの連載の第5回でmatplotlib.pyplotモジュールの関数を使う例を紹介しています。同じことをやっても仕方がないので、ここでは、pandasデータフレームのグラフ描画メソッドを使うことと、どのように結果を見るかということに重点を置くことにします。では、1つずつ見ていきましょう。

データの特徴を可視化する（箱ひげ図でデータの範囲を見る）

　箱ひげ図を作る方法は幾つかありますが、ここでは、以下の2つの方法でやってみます*3。

• データフレームのplot.boxメソッドまたはboxplotメソッドを使う
• Seriesのplot.boxメソッドを使う

*3　pandas.plottingモジュールのboxplot関数にデータフレームまたはSeriesを指定しても箱ひげ図の描画ができます。

　まず、データフレームのboxplotメソッドを使って表示してみます。ただし、築年数と世帯年収をまとめて指定すると、単位が異なるにも関わらず同じ描画領域の中にグラフが表示されてしまいます（リスト17、図11）。

import pandas as pd

df = pd.read_csv('./sample_data/california_housing_train.csv')
bp = df[['housing_median_age', 'median_income']].boxplot()

リスト17　築年数と世帯年収の箱ひげ図を描画するコード（見づらいグラフになってしまう）
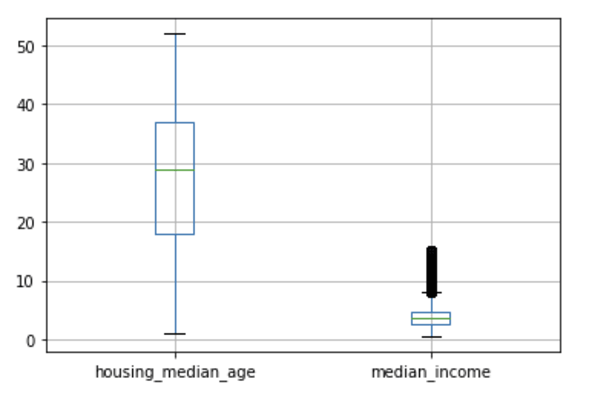
データフレームのboxplotメソッドを呼び出すだけで箱ひげ図が描ける。しかし、単位の異なる列を指定すると、あまり意味のないグラフになってしまう。返り値をbpに代入しているのは、単に、実行結果として返り値を表示せずにグラフだけを表示するため（実行結果は図11）。

図11　リスト17の実行結果（見づらい箱ひげ図）
同じグラフに異なるスケールのグラフを描画してしまったので、世帯年収の箱ひげ図が見づらくなってしまった。箱ひげ図の見方については、次の例で説明する。

　見やすいグラフにするために、築年数と箱ひげ図と世帯年収の箱ひげ図を個別に描いて並べるようにしておきましょう。データフレームのboxplotメソッドやSeriesのplot.boxメソッドは、matplotlib.pyplotモジュールのboxplot関数のラッパー（複雑な部分を隠して使いやすくしたもの）となっているので、お手軽にグラフを描くのに便利です。しかし、複数のグラフを並べるなど、細かな設定を行うためにはmatplotlib.pyplotモジュールの関数が必要になることもあります（リスト18、図12）。

# リスト17の続きに入力する
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 6))
# 築年数の箱ひげ図
plt.subplot(1, 2, 1) # 1行2列の1つ目
bp1 = df.housing_median_age.plot.box(grid=True)

# 世帯収入の箱ひげ図
plt.subplot(1, 2, 2) # 1行2列の2つ目
bp2 = df.median_income.plot.box(grid=True)

リスト18　築年数と世帯年収の箱ひげ図を並べて描画するコード
グラフを並べて表示するためにmatplotlib.pyplotモジュールsubplotメソッドを使って描画領域を指定している。Seriesのplot.boxメソッドを単に呼び出すだけだとグリッド線が表示されない。そのため、grid=Trueを指定してグリッド線が表示されるようにした。

　図12はリスト18を実行して描画された箱ひげ図と、その見方を合わせて示したものです。

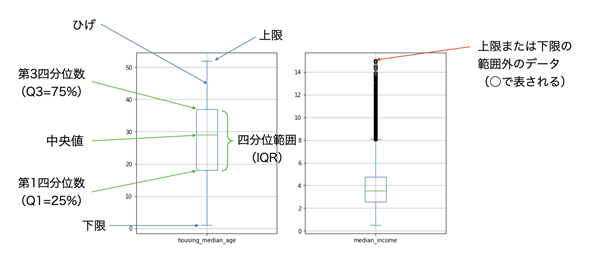
図12　リスト18の実行結果と箱ひげ図の見方（築年数と世帯年収の箱ひげ図を並べて描画）
箱ひげ図では、第1四分位数（Q1）から第3四分位数（Q3）までが「箱」で描かれる。この範囲を四分位範囲（IQR）と呼ぶ。、そこから上限までと下限までが「ひげ」として描かれる。標準の設定では、上限はQ3+1.5×IQR以下の最も近い値の位置に、下限はQ1-1.5×IQR以上の最も近い値の位置になり、短い横線（キャップスラインと呼ばれる）が描かれる。上限や下限からはみ出した値は○で示される。

　箱ひげ図を見ると、築年数の分布にはあまり偏りがないように見えます。ただし、度数（値の個数）が反映されていないので、中央に山がある正規分布のような形になっているかどうかはこれだけでは分かりません（これについては後述します）。一方、世帯年収の方は、小さい方に値が集中していることが分かります。○マークが幾つも重なって表示されているので、極端に離れた外れ値がポツンと存在するのではなく、小さい値の「山」の「裾」を右に引きずるような形で大きな値が並んでいることが分かります。

データの特徴を可視化する（ヒストグラムで度数の分布を見る）

　箱ひげ図だけでは、分布の形がよく分からないので、ヒストグラムを作ってみましょう。ここでは世帯年収のヒストグラムだけを描きます（築年数のヒストグラムの描画と考察については練習問題で取り上げることとします）。ヒストグラムを作るにはデータフレームやSeriesのplot.histメソッドなどを使う方法がありますが、ここでは、単一の列のヒストグラムを作成するので、Seriesのplot.histメソッドを使ってやってみます（リスト19、図13）。

# リスト18の続きに入力する
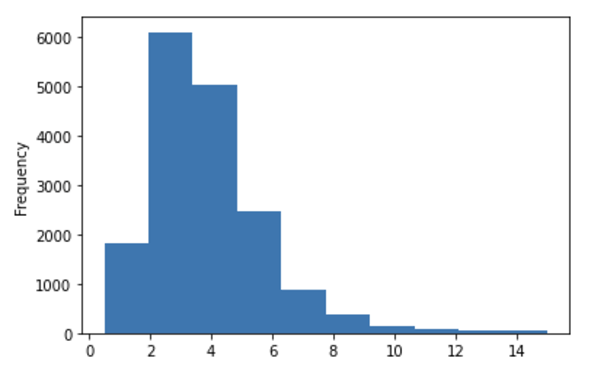
hist = df.median_income.plot.hist()

リスト19　世帯年収のヒストグラムを描画するコード
最も簡単にヒストグラムを描くには、plot.histメソッドを呼び出すだけ。特に何も指定しなければ、階級は10個に分けられる（実行例は図13）。

図13　リスト19の実行結果（世帯年収のヒストグラム）
世帯年収の単位は「万ドル」となっている。2万ドル〜4万ドルあたりが多いことが分かる。

　基本統計量を求めたところで平均値と中央値の関係を紹介しましたが、世帯年収については平均値が3.88万ドル、中央値が3.54万ドルとなっており、平均値＞中央値なので、左に山のある分布だろうと推測されました。図13を見れば確かにそうなっていることが分かります。

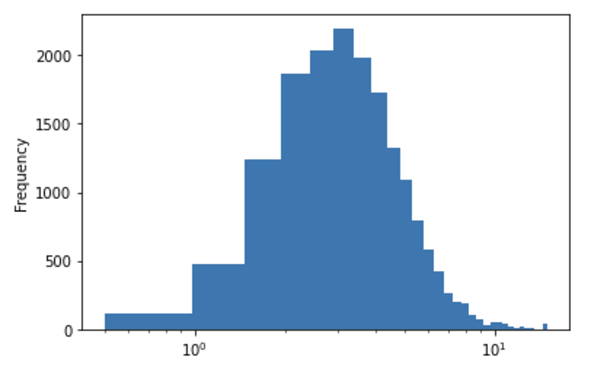
　機械学習（回帰や分類）を行う場合には、分布が偏っていると予測の精度が上がらないことがあります。図13のように左に山のある分布の場合、各データの対数を取ると正規分布に近い形になります。機械学習では、そのように変換した値を使うこともよくあります*4。plot.histメソッドではX軸やY軸を対数変換したグラフが描けるので、その形を見てみましょう（リスト20、図14）。

*4　機械学習のためのライブラリscikit-learnでは、分布の歪みを正規分布に近い形に変換するためのツールとして、sklearn.preprocessing.PowerTransformerクラスが用意されており、yeo-johnson変換やbox-cox変換と呼ばれる方法が使えます。また、値が一定の範囲に収まるように変換する正規化や標準化も行われます。例えば、最小値が0、最大値が1になるように変換するにはMinMaxScalingクラスを使い、平均が0、分散が1の正規分布になるように変換するにはStandardScalingクラスを使います（後述します）。

# リスト19の続きに入力する
hist = df.median_income.plot.hist(logx=True, bins =30)

リスト20　世帯年収のヒストグラムを描画するコード（X軸を対数変換し、階級を30に分けた）
各データの値はX軸の値なので、X軸を対数変換する（Y軸は度数）。対数変換するには、logx=Trueという引数を指定すればよい。なお、ここでは、もう少し細かく区切って見るために階級の個数を引数binsに指定し、30個にしてみた。

図14　リスト20の実行結果（X軸を対数変換した世帯年収のヒストグラム）
分布が左に偏っている場合、X軸を対数軸にすると正規分布に近い形になる。

　階級の個数によっては、ヒストグラムの形が違って見えることがありますが、大まかな分布を把握することはできます。なお、階級の個数を幾つにするかは、スタージェスの公式（log₂n＋1）によって求めた値が目安とされることがあります。ここでの例であれば、n＝17000なので、log₂17000＋1 ≈ 15となります。

データの特徴を可視化する（散布図で変数同士の関係を見る）

　これまでのお話は、個別の列（変数）について特徴を見るものでした。列同士の関係についてはそれだけでは分かりません。すでに求めた相関行列は列同士の関係を表すものですが、その特徴がよく分かるように散布図を作成して列同士の関係を可視化してみましょう。散布図は、データフレームのplot.scatterメソッドを使えば簡単に描画できますが、全ての変数同士の散布図を一度に描画するにはpandasのplotting.scatter_matrix関数が便利です（リスト21）。

# リスト20の続きに入力する
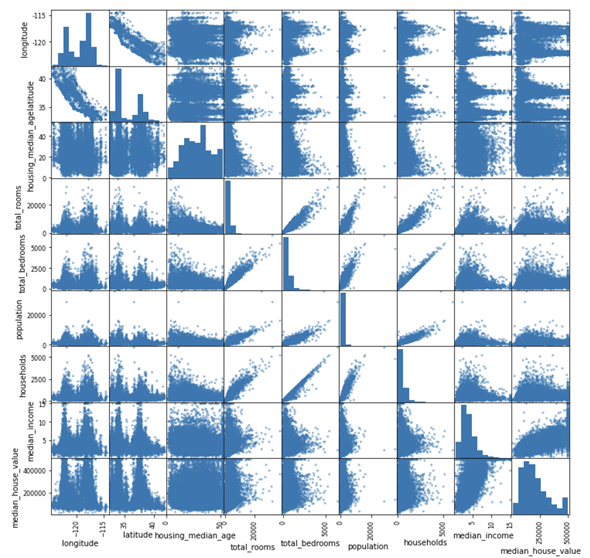
sc = pd.plotting.scatter_matrix(df, figsize=(12, 12))

リスト21　全ての変数同士の散布図を一括描画するコード
plotting.scatter_matrix関数にデータフレームを指定すれば全ての変数（列）同士の散布図が描かれる。ここでは、図のサイズを横12インチ、縦12インチとした。

　plotting.scatter_matrix関数では、データフレームの列数やデータの件数が多くなると処理にかなりの時間がかかります（図15の結果を得るのに、筆者の環境では15秒かかりました）。同じ列同士については、散布図ではなくヒストグラムが描かれるので、分布も合わせて全体像を見るのにも便利です。

図15　リスト21の実行結果（全ての変数同士の散布図）
対角線上のグラフはヒストグラムになっているのでその項目の分布が分かる。それ以外の部分が散布図となっており、列同士の関係が可視化できる。

　ちなみに、個々の列同士の散布図を描画するには、データフレームのplot.scatterメソッドを使って、

sc = df.plot.scatter('median_income', 'median_house_value')

のように書きます。

　この記事では、個々のヒストグラムを描画する例を先に紹介しましたが、実際には、最初に図15のような全てのグラフを作成しておき、気になる箇所について詳細に見ていく、といった順序で分析を進めていったほうがいいでしょう。例えば、全体を眺めてみると、住宅価格のヒストグラム（図15の右下）がどうも不自然です。右端（500,000ドルあたり）の値がやけに多いですね。これはおそらく、値の大きなデータをひとまとめにしてしまったからだと思われます。築年数についても、箱ひげ図では偏りがなかったように見えましたが、山が2つあるようにも見えます。これらの項目は詳細に見ていく必要がありそうです（目標4で重回帰分析を行うときに見ることにします）。

コラム　地図を使ってデータを可視化する

　図15を見ると、経度と緯度に山が2つあることが分かります。これは、住宅が集中して存在する場所（＝大都市）があるということです。大都市ほど人口や世帯収入が大きいと考えられ、それらと住宅価格には正の相関があるので、地域によって住宅価格の差があることも想像できます。そこで、地図上で住宅データの分布と住宅価格を色分けして表示してみましょう（リスト22、図16）。

　データを地図上にマッピングするにはGeoPandasライブラリが便利です。詳細はこちらのサイトを参照してください。リスト22を実行するには、あらかじめ以下のコードを実行しておき、geopandasモジュールをインストールしておく必要があります。

!pip install geopandas

　地図データはU.S. Geological Surveyのサイトの「Type: Download」の下のリンクなどから入手できるので、その地図に住宅データをマッピングしていきます。上記のサイトからダウンロードした地図データのファイルはzipファイルとなっているので、それを展開して得られる「GU_CountyOrEquivalent」というファイル（名前が同じで拡張子が異なる.dbf、.prj、.shp、.shxとなっている4つのファイル）をGoogle Colabで利用できるようにしておきましょう。そのためには以下のコードを実行しておくのが簡単です（実行にはやや時間がかかります。複数回実行すると、同じファイルが何度もダウンロードされるので、実行は1回だけで構いません）。

!wget https://prd-tnm.s3.amazonaws.com/StagedProducts/GovtUnit/Shape/GOVTUNIT_California_State_Shape.zip
!unzip GOVTUNIT_California_State_Shape.zip

　準備ができたらリスト22のコードを実行してみましょう。図17のような地図が表示されるはずです。

import pandas as pd
import geopandas as gpd
from mpl_toolkits.axes_grid1 import make_axes_locatable

# データを読み込む
df = pd.read_csv('./sample_data/california_housing_train.csv')
# 地図データを読み込む
map = gpd.read_file('./Shape/GU_CountyOrEquivalent.shx')  # データはあらかじめGoogle Colabで利用できるようにしておく
# 経度と緯度の列を位置データに変換し、データフレームの末尾に追加する
gdf = gpd.GeoDataFrame(df, geometry=gpd.points_from_xy(df.longitude, df.latitude))

# 地図を描く
ax = map.plot(color='aliceblue', edgecolor='black', figsize=(8, 8))
# 凡例（カラーバー）を描く領域を用意する
divider = make_axes_locatable(ax) # 描画領域を追加できるようにする
cax = divider.append_axes('right', size='5%', pad='2%') # 右に、5%の大きさ、2%の空き
# 住宅データをプロットする（axが地図、caxがカラーバー）
gax = gdf.plot(column='median_house_value', ax=ax, cax=cax, legend=True, marker='.', markersize=10)

リスト22　住宅データを地図上にプロットするコード
地図データをgeopandasモジュールのread_file関数で読み込んだ後、GoeDataFrame関数により、地図情報を表すデータフレームgdfを作成する。地図情報は、geopandasモジュールのpoints_from_xy関数を使って緯度と経度を位置データに変換し、元のデータフレーム（df）の後の列に追加したものになっている。gdfのplotメソッドを使って、gax = gdf.plot(ax=ax)とすれば住宅の位置が地図上にプロットできる。ここでは、引数にcolumn='median_house_value'を指定し、色分けするのに使う列を指定している。axは地図を描く領域、caxは凡例を描く領域。

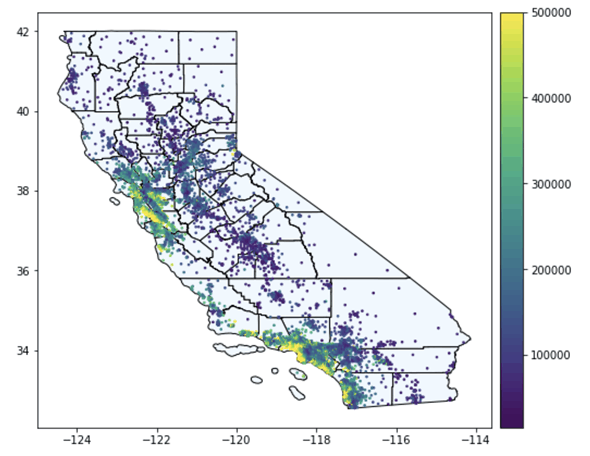
図16　リスト22の実行結果（住宅を地図上にブロット）
地図上に住宅データをプロットすると、どのあたりに住宅が集中しているかが分かる。住宅価格を色分けしてプロットしたので、どの地域の価格が高いかということも分かる。

　カラーバーで示されているように、黄色で表示されている地域の住宅価格が高くなっています。住宅価格の高い地域は、サンフランシスコ、サンノゼあたり（左上の黄色い部分）とロサンゼルス、サンディエゴあたり（右下の黄色い部分）です。ちなみに、これらの都市はカリフォルニア州の人口の多い都市の上位4つになっています。