Pythonで統計・データ分析！〜基本統計量の活用と機械学習の基本：数学×Pythonプログラミング入門（5/5 ページ）

データ分析において最もよく使われる表形式のデータを取り扱う方法を見ていく。まず、pandasデータフレームの基本的な取り扱い方法を確認し、次に、各種の基本統計量を求める。また、基本統計量の可視化を行い、データの「見方」についても触れる。最後に、scikit-learnを使った回帰と分類の簡単な例を紹介する。

[羽山博，著]

練習問題

　では、練習問題です。問題の考え方について解説した動画も用意してあります。ぜひご視聴ください。

動画4　統計／データ分析の練習問題

（1）築年数のヒストグラムを作成する

　カリフォルニアの住宅価格データを使って、築年数（housing_median_age）のヒストグラムを作成してください。階級数は20とします。また、最大値と等しい値が幾つあるか求めてみてください（答えは1052件です）。さらに、得られた結果に考察も加えてみましょう。

（2）築年数が52年以上のデータを除外して重回帰分析を行う

　練習問題（1）では、築年数の最大値が1052件もあることが分かります（最大値の値は52です）。つまり、築年数が52以上のデータはひとまとめにされているというわけです。目標4で住宅価格が500,001以上のデータを除外しましたが、築年数が52以上のデータも除外して重回帰分析を行ってみてください。RMSEがどれぐらい改善したかも確認しておきましょう。

（3）新たな特徴量を作成して重回帰分析を行う

　これまで見てきた「部屋数」は、その区画の合計の値でした。世帯数（households）が多ければおのずと部屋数も多くなります。そこで、1世帯数あたりの部屋数を求め、それを特徴量として使って重回帰分析を行ってみてください。つまり、説明変数は、築年数（housing_median_age）、世帯収入（median_income）、新たに作成した1世帯当たりの部屋数（rooms_per_householdsという項目名としましょう）の3つになります。RMSEがどれぐらい改善したかも確認しておきましょう。

　ヒント：pandasのデータフレームやSeriesでは、NumPyのブロードキャスト機能と同様の機能が使えるので、列同士の四則演算も可能です。データフレームに列（Series）を挿入するには、insertメソッドの引数に、挿入する列位置、見出し、データを指定します。

練習問題の解答例

　以下、解答とプログラムの作成例です。もちろん、異なるやり方もあるので、これらが唯一の答えというわけではありません。

（1）築年数のヒストグラムを作成する

　リスト19の例を参考にすれば簡単にできますね。最大値と同じ値の個数を求めるコードも、リスト23で重回帰分析を行った後の考察を参考にすれば簡単に書けます。オレンジ色の部分をクリックまたはタップすると答えが表示されます。

import pandas as pd

df = pd.read_csv('./sample_data/california_housing_train.csv')

hist = df.housing_median_age.plot.hist(bins=20)
print((df.housing_median_age == df.housing_median_age.max()).sum())
# 出力例：
# 1052

リスト26　築年数のヒストグラムを作成し、まとめられたデータの件数を表示する
df.列見出しと書けば特定の列が取り出されるので、築年数の列を取り出し、ヒストグラムを描くためのメソッドを指定すればよい。また、築年数が、築年数の列の最大値と等しいかどうかを調べ、Trueの個数を数えれば、何件のデータがひとまとめにされているかが分かる。

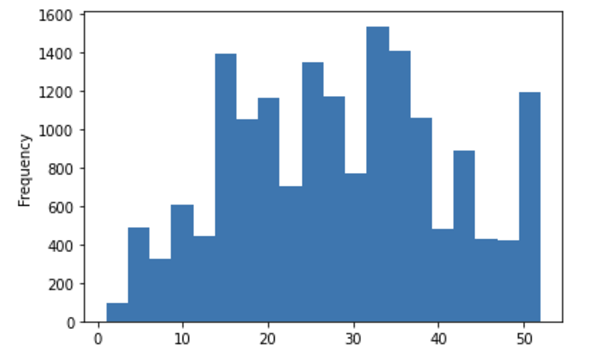
図17　リスト23の実行結果（住宅を地図上にブロット）
築年数が大きなデータがまとめられていることがグラフからも読み取れる。また、山が幾つかあることも分かる。16年、26年、34年あたりに山があることから、8〜10年ごとの景気循環を反映しているのかもしれないということが読み取れる。

（2）築年数が52年以上のデータを除外して重回帰分析を行う

　これは簡単です。リスト24で見たコードを変更し、条件を追加するだけでできます。コード全体を掲載しておきます。オレンジ色の部分が追加した部分です。クリックまたはタップすると答えが表示されます。

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

df = pd.read_csv('./sample_data/california_housing_train.csv')
df = df.query('housing_median_age < 52 and median_house_value < 500001') # この行を変更した
x = df[['housing_median_age', 'total_rooms', 'population', 'median_income']]
y = df['median_house_value']

x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)

model = LinearRegression()
model.fit(x_train, y_train)

y_train_pred = model.predict(x_train)
y_test_pred = model.predict(x_test)
print('訓練データのRMSE:', mean_squared_error(y_train, y_train_pred, squared=False))
print('テストデータのRMSE:', mean_squared_error(y_test, y_test_pred, squared=False))
# 出力例：
# 訓練データのRMSE: 69904.65682068754
# テストデータのRMSE: 70499.54679916702

リスト27　築年数と住宅価格のまとめられたデータを除外して重回帰分析を行う
築年数が52以上のデータと、住宅価格が500,001以上のデータを除外した。リスト24で住宅価格についてまとめられたデータを除外した場合は、RMSEが7万ドルを数千ドル超えるぐらいだったが、この例では7万ドル台に改善されている。

（3）新たな特徴量を作成して重回帰分析を行う

　1世帯あたりの部屋数はdf.total_rooms / df.householdsで求められます。築年数と世帯収入からなるデータフレームの末尾に、1世帯あたりの部屋数の列を挿入すれば、あとはこれまでに見たコードと全く同じです。

import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# データを読み込み、説明変数と目的変数を用意する
df = pd.read_csv('./sample_data/california_housing_train.csv')
df = df.query('housing_median_age < 52 and median_house_value < 500001')
x = df[['housing_median_age', 'median_income']]
x1 = df.total_rooms / df.households # 1世帯あたりの部屋数という特徴量x1を作成する
x.insert(2, 'rooms_per_households', x1) # 2列目にx1を挿入する
y = df['median_house_value']
# 訓練データとテストデータに分ける
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0)

# 重回帰分析を行う（線形回帰モデルを当てはめる）
model = LinearRegression()
model.fit(x_train, y_train)

# 予測値を求め、RMSEの値を表示する
y_train_pred = model.predict(x_train)
y_test_pred = model.predict(x_test)
print('訓練データのRMSE:', mean_squared_error(y_train, y_train_pred, squared=False))
print('テストデータのRMSE:', mean_squared_error(y_test, y_test_pred, squared=False))
# 出力例：
# 訓練データのRMSE: 69764.3506176689
# テストデータのRMSE: 70242.39017594406

リスト28　世帯あたりの部屋数という特徴量を作成して重回帰分析を行う
データフレームのinsertメソッドを使って、新しい特徴量を2列目（末尾の列）に挿入した。リスト27の結果と比較すると、RMSEの値が200ドル程度改善された。

　1世帯当たりの部屋数を末尾に追加するには、以下のようにx1をデータフレームにし、pandasのconcat関数を使ってデータフレームを連結してもできます。axis=1は列を連結する（横方向に連結する）という指定です。

x1 = pd.DataFrame({'rooms_per_households': df.total_rooms / df.households})
x = pd.concat([x, x1], axis=1)

---

　……というわけで、今回は、データの取り扱いやデータの見方という切り口で、基本統計量を求め、可視化を行いました。応用例として、機械学習についても触れましたが、回帰や分類のために利用できるさまざまなモデルや機能よりも、どのようにデータを見るかということに重点を置きました。

　さて、この連載も今回が最終回となりました。不定期の更新でしたが、長く間ご愛読くださってありがとうございました。ただ、中学／高校数学とPythonプログラミングについて、取りこぼした話題もまだまだあるので、折に触れて番外編を追加できればと思っています。

「数学×Pythonプログラミング入門」