[NumPy超入門]内積、行列積からコサイン類似度までNumPyを使って試してみよう:Pythonデータ処理入門(2/2 ページ)
内積や行列積、アダマール積などさまざまな種類がある行列の積とそれらを計算する関数、2つのベクトル(行列)が似ているかどうかを判定できるコサイン類似度について触れてみよう。
numpy.dot関数
numpy.dot関数はベクトルや行列の「ドット積」を求める関数です。といっても要するにこの関数もまたベクトルの内積を求めたり、二次元配列の行列積を求めたりするのに使えるということです(数学の世界では、これらの演算を「A・B」などのようにドット「・」を用いて記述し、「dot product」「ドット積」などと呼んでいます。このことから「dot」という名前を付けているのでしょう)。
ただし、NumPyのドキュメントには以下のような記載もあります(筆者による適当訳です)。
- 両者が二次元配列であれば、ドット積とは行列積のことであるが、numpy.matmul関数または(@演算子を用いて)「a @ b」とする方が好ましい
- どちらかがスカラー値であれば、それはnumpy.multiply関数呼び出しに等しく、numpy.multiply(a, b)またはa * bの方が好ましい
今回は積を求める対象をベクトルと行列に絞っています。そのため、ベクトルの内積を求めるのであればnumpy.dot関数を使えばよいのですが、行列積を求めるのであればnumpy.matmul関数や@演算子を使用することが、またスカラー倍を求めるのであればnumpy.multiply関数や*演算子を使用することが望ましいということです。
とはいえ、Webを検索してもnumpy.dot関数は広く使われていますし、numpy.matmul関数との振る舞いの違いは三次元以上の配列を渡したときになります。上の注記をきちんと頭に入れた上で、ベクトルや行列が対象であれば、numpy.dot関数を使うのは構わないでしょう(ただし、numpy.dot関数はベクトルの内積や行列の行列積を計算する汎化された名前であり、個々の関数を使った方が、自分が何を意図してこのコードを書いたのかをコードの中で明確に示せることには注意しましょう)。
というわけで、以下に例を示します。作成しているベクトル/配列はこれまで通りなので特に説明の必要はないでしょう。
a = np.array([1, 2, 3])
b = np.array([2, 2, 2])
c = np.dot(a, b) # ベクトルの内積を求める
print(c) # 12
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = np.dot(a, b) # 行列積を求める
print(c)
#[[19 22]
# [43 50]]
なお、numpy.dot関数と同様な計算を行うnumpy.ndarray.dotメソッドもあります(numpy.matmul関数、numpy.multiply関数、 この後で紹介するnumpy.inner関数にはそうしたメソッドはありません)。このメソッドを使うと、上のコードは次のようにも記述できます。
a = np.array([1, 2, 3])
b = np.array([2, 2, 2])
c = a.dot(b) # ベクトルの内積を求める
print(c)
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = a.dot(b) # 行列積を求める
print(c)
numpy.inner関数
numpy.inner関数は、2つのベクトルの内積を求める関数です。二次元以上の配列も渡せるんでしょ、と思った方もいるでしょう。その通りです。ただし、そのときの動作はこれまでに紹介してきた関数とは異なっている点には注意してください。
以下に例を示します。
a = np.array([1, 2, 3])
b = np.array([2, 2, 2])
c = np.inner(a, b)
print(c) # 12
この例ではベクトル(一次元配列)をnumpy.inner関数に渡しています。そのため、これまでの例と同様にその内積の値である12が返されています。
次に行列をnumpy.matmul関数に渡したときと、numpy.inner関数に渡したときの振る舞いの差を確認してみましょう。
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
c = np.matmul(a, b) # 行列積の計算
print(c)
# 出力結果:
#[[19 22]
# [43 50]]
c = np.inner(a, b) # 最後の軸に沿って積和を計算
print(c)
# 出力結果:
#[[17 23]
# [39 53]]
numpy.matmul関数に渡したときにはこれまで通り、行列積が得られています。が、numpy.inner関数に渡したときには、戻ってくる行列の値がそれとは異なっています。そこでnumpy.inner関数のドキュメントを見てみると「(一次元配列よりも)次元が高いときには、最後の軸に沿った積和となる」と書いてありました(筆者の適当訳です)。
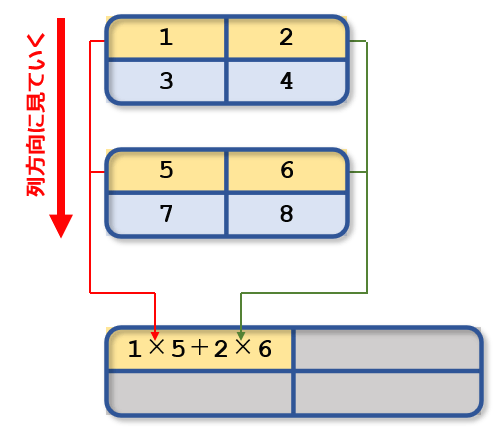
これだけ読んでもちょっと分かりにくいのですが、以下の図に示すようなものだと考えればよいでしょう。
この場合、最後の軸とは列です。よって、列方向に眺めて、上の図に示したような対応関係で積を取り、それらを加算した結果を含んだ配列が戻り値になるということです。この図は最初の計算だけを示していますが、次は1つ目の配列の第1行と2つ目の配列の第2行で同様な計算を行って求めた積和が結果の行列の第1行第2列の値になります。残りも同様です。
ここで見たnumpy.matmul関数とnumpy.inner関数のように、特定の条件下でのそれぞれの関数の振る舞いは異なるので、どの関数を使えばよいかは、そのときどきに応じて自分が何をしたいのかを把握して、それに合致したものを選ぶようにする必要があります。
行列の絶対値とコサイン類似度
最後にひとつ、ベクトルや行列の積とは異なりますが、それらの大きさ(絶対値、原点からの距離)を求める関数を簡単に紹介しましょう。それはnumpy.linalg.norm関数です。詳しいことまではご紹介できませんが、以下のコードを見てください。
a = np.array([1., 1.])
d = np.linalg.norm(a)
print(d) # 1.4142135623730951
なじみのある値が表示されました。これはベクトル(1, 1)の大きさともいえますし、座標(1, 1)の原点からの距離ともいえます。いずれにしろ、このベクトルの大きさは1.41421356……ということです。
そして、numpy.linalg.norm関数が返す値と内積を組み合わせることで「コサイン類似度」と呼ばれる値を計算できるのです。コサイン類似度とは2つのベクトルがどのくらい似ているかを示す値で、その取り得る値の範囲は−1〜1となっています。1に近いほど2つのベクトルは似ていることを、-1に近いほど2つのベクトルは似ていないことを示します(0なら2つのベクトルは直行していて、関係がないことを意味します)。
機械学習やディープラーニングの世界では、コサイン類似度はある文章と別の文章が似た意味のものかどうかや、ある単語と別の単語が似た概念を指しているのかどうかなどを調べるために(少なくとも内部的には)よく使われています。
詳しい説明は上のリンクを参照していただくとして、コサイン類似度を計算するコードをここでは自分で書いてみることにしましょう。2つのベクトルをa、bとすると「コサイン類似度=aとbの内積/(aの大きさ×bの大きさ)」で算出できます。以下がこれをPythonのコードに落とし込んだものです。
def calc_cos_similarity(x, y):
dot_product = np.dot(x, y)
abs_x = np.linalg.norm(x)
abs_y = np.linalg.norm(y)
cos_similarity = dot_product / (abs_x * abs_y)
return cos_similarity
ここではベクトルの内積を求めるということでnumpy.dot関数を使っていますが、numpy.matmul関数でも結果は変わりません。次にnumpy.linalg.norm関数を使って関数に渡された2つのベクトルの大きさを計算しています。後は先ほどの「コサイン類似度=aとbの内積/(aの大きさ×bの大きさ)」という式を計算しているだけです。
以下では3つのベクトル(1.0, 1.0)、(-1.0, -1.0)、(1.0, -1.0)を用意して(それぞれa、b、c)、aとb、aとcのコサイン類似度を判定しています。
a = np.array([1., 1.])
b = np.array([-1., -1.])
c = np.array([1., -1.])
cos_similarity = calc_cos_similarity(a, b)
print(cos_similarity) # -0.9999999999999998
cos_similarity = calc_cos_similarity(a, c)
print(cos_similarity) # 0.0
aとbの比較、つまり(1.0, 1.0)と(-1.0, -1.0)は完全に逆向きのベクトルなので、コサイン類似度は-1に近い値が出そうです。そして、まさにその通りの結果になっています。また、aとcの比較、つまり(1.0, 1.0)と(1.0, -1.0)は2つのベクトルが直行しているのでコサイン類似度は0になりました。コサイン類似度の観点でいえば、aとcの間に関係はないということです。
といったように、ベクトルや行列の積を使うとこんなこともできるんだということを感じていただけたら幸いです。次回はもう少し行列に関連するアレやコレをご紹介する予定です。
Copyright© Digital Advantage Corp. All Rights Reserved.