[NumPy超入門]平均/中央値/最頻値や分散/標準偏差を求めてみよう:Pythonデータ処理入門
NumPyが提供する基本統計量を調べるさまざまな関数を使って、サンプルデータにはどんな特徴があるかを調べてみましょう。
連載概要
本連載はPythonについての知識を既にある程度は身に付けている方を対象として、Pythonでデータ処理を行う上で必須ともいえるNumPyやpandas、Matplotlibなどの各種ライブラリの基本的な使い方を学んでいくものです。そして、それらの使い方をある程度覚えた上で、それらを活用してデータ処理を行うための第一歩を踏み出すことを目的としています。
前回はある行列の逆行列、行列式、固有値と固有ベクトルを求めるお話をしました。今回は多数のデータがどんな特徴を持っているのかを調べるのに役立つ基本統計量をNumPyで取り扱う方法を見ていきます。
基本統計量とは
基本統計量とは、何らかのデータセットがあったとき、それらにはどのような特徴があるかを示す値のことです。というと分かりにくいのですが、平均値、最大値、最小値、標準偏差と分散などの値を用いることで、データがどのように分布しているかなどを調べることができるでしょう。NumPyには、そうした値を調べるための関数やメソッドが用意されています。以下に一部ですが、そうした関数/メソッドを列挙します。
| 関数 | 説明 |
|---|---|
| numpy.max関数/numpy.ndarray.maxメソッド | 指定された軸に沿って配列の要素から最大値を返す |
| numpy.min関数/numpy.ndarray.minメソッド | 指定された軸に沿って配列用の要素から最小値を返す |
| numpy.sum関数/numpy.ndarray.sumメソッド | 指定された軸に沿って配列の要素の和を計算する |
| numpy.mean関数/numpy.ndarray.meanメソッド | 指定された軸に沿って算術平均を計算する |
| numpy.average関数 | 指定された軸に沿って重み付きの算術平均(加重平均)を計算する |
| numpy.median関数 | 指定された軸に沿って配列の要素の中央値を計算する |
| numpy.std関数 | 指定された軸に沿って配列の標準偏差を計算する |
| numpy.var関数 | 指定された軸に沿って配列の分散を計算する |
| 基本統計量を求める関数/メソッド(一部) | |
これらの他にもパーセンタイル(百分位数)、クォンタイル(四分位数)を求める関数、配列の要素の積を求める関数などもありますが、今回は上記の関数/メソッドについて見てみることにしましょう(NumPyには最頻値を直接求める関数は用意されていません)。
なお、以下では以下のコードでサンプルとなる2次元配列を作成します。
import numpy as np
scores = np.array([[74, 27, 64, 51, 61],
[58, 38, 72, 33, 57],
[79, 28, 76, 49, 54],
[60, 63, 58, 28, 71],
[55, 50, 62, 41, 64],
[39, 54, 49, 29, 53],
[45, 56, 50, 31, 36],
[29, 40, 53, 25, 92],
[49, 51, 69, 44, 51],
[67, 22, 64, 51, 59]])
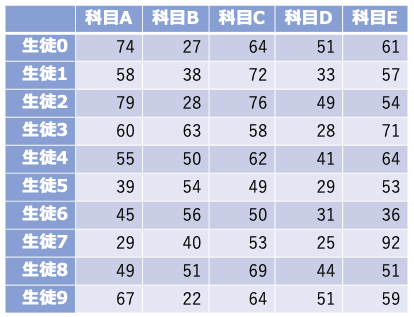
これは10人の生徒の試験結果(5科目)をまとめたものだと考えてください(各科目100点満点)。
各行が1人分の試験結果を表し、各列は科目ごとの点数となります。ただし、NumPyでは列や行に名前(文字列)を与えるのが難しいので、ここでは科目Aとか生徒0のようなラベル(列名、行名)はなしで、得点のみが二次元配列に格納されていると考えてください。このデータに対して、上で紹介した関数/メソッドを適用しながら、このデータの特徴を見ていくことにします。
最大値と最小値
最大値と最小値については第5回で取り上げましたからここでは簡単に見ておきます。
numpy.max関数とnumpy.min関数を使うと、以下のように簡単に試験の最高得点と最低得点が得られます。
result = np.max(scores)
print(result) # 92
result = np.min(scores)
print(result) # 22
しかし、これでは全科目における最高得点と最低得点が1つだけしか得られていません。このようなときにはaxisパラメーターに列に沿って計算をするのか(axis=0)、行に沿って計算をするのか(axis=1)を指定するとよいでしょう。列に沿うとは特定の科目における最高得点/最低得点を調べるということであり、行に沿うとは個人個人の最高得点/最低得点を調べるということになります。
科目ごとの最高得点/最低得点を調べる例を以下に示します。
result = np.max(scores, axis=0)
print(result) # [79 63 76 51 92]
result = np.min(scores, axis=0)
print(result) # [29 22 49 25 36]
先ほどは最高得点と最低得点がどちらも1つだけ返されましたが、今度は一次元配列に値が返されてきました。要素数が5なのは、科目数と同じであることを意味しています。
試験というのは、特定の試験範囲について生徒がどれだけ内容を理解しているかを把握するためのものです。そのことを考えると、科目Dは最高得点が51点で最低得点も25点とかなり低いことから試験が難しすぎた、あるいはここまではちゃんと学んでほしいというラインに生徒の理解が及んでいない可能性があります(つまり、何らかの形で教師から生徒に対してフォローの必要があるでしょう)。
対して、科目Cは最高得点が79点で最低得点が49点です。こちらは点数のばらけ具合(分散)が狭くなっているので、多くの生徒がそれなりに内容を理解してくれたものだと考えられますね。
なんてことを書いていますが、このデータは筆者が適当に作ったものなので、それがホントかどうかなど誰にも分かりません(笑)。とはいえ、最高得点と最低得点を取り出すだけでも、(架空の)データを基にそれなりの検討ができることは分かりました。
では、生徒個人の最高得点/最低得点を調べるコードを以下に示します。
result = np.max(scores, axis=1)
print(result) # [74 72 79 71 64 54 56 92 69 67]
result = np.min(scores, axis=1)
print(result) # [27 33 28 28 41 29 31 25 44 22]
axis=1を指定しているので、今度は行に沿って(個人個人の)最高得点と最低得点が得られます。今度も一次元配列が返されていますが、今度は生徒数(10人)に対応して、その要素数は10となっています。この結果を見ると生徒4(最高得点が64点、最低得点が41点)と生徒8(最高得点が69点、最低得点が44点)は全ての科目でそれなりの得点を取っていることが予想できますから、それなりの理解度で試験を迎えたといえるのかもしれません。他の生徒については得意科目と不得意科目の差が大きい、ヤマが外れたなどの要素が考えられます(この検討はもちろん架空のデータを基にしています)。
合計値
合計値はnumpy.sum関数またはnumpy.ndarray.sumメソッドで得られます。ここでもaxisパラメーターで合計をどの軸に沿って計算するかを指定できます。指定しなければ、全ての要素の合計が得られますが、それはあまり意味がないことでしょう。同様に科目ごとに合計を計算するのもあまり意味があるとは思えません。そこで、ここでは生徒個人の合計を取ってみます。これは総合成績を付けるという意味では有用です。
result = np.sum(scores, axis=1)
print(result) # [277 258 286 280 272 224 218 239 264 263]
result = scores.sum(axis=1)
print(result) # [277 258 286 280 272 224 218 239 264 263]
このように簡単に合計得点も求められます(合計で500点満点なのですが、300点を取れているデータがないことに気が付いて、もう少しデータの作りを考えるべきだったと思っています……)。
平均値
平均値はnumpy.mean関数かnumpy.ndarray.meanメソッド、またはnumpy.average関数で求められます。前者の2つと後者が異なるのはnumpy.average関数は加重平均を求めることにも使える点です(後述)。
axisパラメーターを指定しなければ、これまでの関数と同様、全ての要素を対象として平均値を計算します。axisパラメーターを指定すると、指定した軸に沿って平均値を求めます。
ここではnumpy.mean関数を使って、科目ごとの平均得点を求めてみましょう。
result = np.mean(scores, axis=0)
print(result) # [55.5 42.9 61.7 38.2 59.8]
やはり科目Dの平均点がかなり低いことが分かります。科目Cと科目Eは約6割の得点率なので生徒はそれなりに理解をしてくれていたようです。
同じことはnumpy.ndarray.meanメソッドでも行えます。
result = scores.mean(axis=0)
print(result) # [55.5 42.9 61.7 38.2 59.8]
もちろん、numpy.average関数も重みを特に指定しなければ、同じ結果となります。
result = np.average(scores, axis=0)
print(result) # [55.5 42.9 61.7 38.2 59.8]
では重みとは何かというと、平均を取る要素(列または行)の重要度を数値で表したものです。ここでは話を単純にして、2つのクラスで何かの試験を行った結果の平均得点が次のようなものだったとしましょう。
s = np.array([60, 75])
一方のクラスの平均点は60点で、もう一方のクラスの平均点が75点だったとします。しかし、60点のクラスには38人の生徒がいて、75点のクラスには22人の生徒しかいなかったとします。このとき、単純に60点と75点を足して2で除算したものを全体の平均としてよいのでしょうか。そうではなく、60点×38人=2280点と75点×22人=1650点を足して、全体の人数(38+22)で割った方が平均点の算出方法としては正しそうな気がします。これを行うのが加重平均の計算です。ここでは人数の差が全体に及ぼす影響を低減するために行っていますが、実際にはさまざまな要素が重みとして考えられる点には注意してください。
result1 = np.average(s)
result2 = np.average(s, weights=(38, 22))
print(f'average: {result1}') # average: 67.5
print(f'weighted average: {result2}') # weighted average: 65.5
result1には通常の平均値が返されます。result2の計算ではクラスの人数を重みとして「weights=(38, 22)」のような指定を行っています。これにより、2つの異なる平均が得られました。75点のクラスが特進クラスで、60点のクラスが普通科クラスだとすると、学校全体の平均としてはそれぞれのクラスの人数までを考慮したものがより適切かもしれません。
中央値
中央値とは、データの集団を昇順(または降順)に並べたときに中央に位置する値のことです。上で見た平均値、後で紹介する最頻値とともにデータの集団を代表する値として扱われることがよくあります(後述)。なお、平均値/中央値/最頻値の詳細な説明は「平均値(Mean)/中央値(Median)/最頻値(Mode)とは?」を参照してください。
データが奇数個のときには1つになりますが、偶数個の場合は中央に位置する2つのデータの平均値とするのが一般的です。NumPyでは中央値はnumpy.median関数で得られます。このとき、元の配列を並べ直す必要はありません。
簡単な例を紹介しましょう。
a = np.array([8, 3, 2, 3, 5, 1, 8]) # 奇数個
print(a) # [8 3 2 3 5 1 8]
b = np.array([6, 4, 8, 5, 2, 1, 3, 1]) # 偶数個
print(b) # [6 4 8 5 2 1 3 1]
このように奇数個の一次元配列と偶数個の一次元配列があったとします。このときに、中央値がどうなるかを確認してみましょう。分かりやすいように配列を昇順に並べたものも表示しておきます。
result = np.median(a)
print(result) # 3.0
print(sorted(a)) # [1, 2, 3, 3, 5, 8, 8]
result = np.median(b)
print(result) # 3.5
print(sorted(b)) # [1, 1, 2, 3, 4, 5, 6, 8]
最初の例では要素は7個なので、中央値は真ん中の3(が浮動小数点数値になったもの)になります。次の例では要素は8個なので、中央値は真ん中にある3と4の平均である3.5になります。
では、今度も科目ごとに中央値を調べてみましょう。
result = np.median(scores, axis=0)
print(result) # [56.5 45. 63. 37. 58. ]
今回はデータが適当にばらけている(ように筆者には見える)ので、中央値はそれなりの値(50点前後)となっています(科目Dについては低いのですが、これは上で見たように最高得点が51点と低いためです)。
このデータでは中央値にはそれほど意味がないようにも思えます。しかし、2人の生徒だけが高い点を取り(97点と82点)、他の生徒があまり点を取れなかったときのことを考えてみてください。
a = np.array([5, 17, 24, 97, 35, 33, 28, 36, 14, 82])
この状況で平均値を計算すると次のようになります。
result = np.mean(a)
print(result) # 37.1
平均値は37.1と十分に低いように思えます。しかし、97点と82点以外の要素だけで平均を取ってみましょう。
b = np.array([5, 17, 24, 35, 33, 28, 36, 14])
result = np.mean(b)
print(result) # 24.0
もっと低い値が得られました。2人の高得点が全体の平均値を10点以上も押し上げています。これはこれで正しい平均かもしれませんが、データの集団を正しく代表しているとはいいにくいかもしれません。では、ここで中央値を調べてみましょう。
result = np.median(a)
print(result) # 30.5
こちらの方が平均値よりもより集団の特徴(高得点を取れた人が少ない)を表しているかもしれません。このように、一部のデータが集団全体に及ぼす影響を軽減するのに中央値は有効です。
最頻値
先ほど述べた、集団を代表するもう一つの値である「最頻値」についても簡単に紹介しておきます。最頻値とは、データの中で最もよく現れる値のことです。データがどのように分布しているかによりますが、正規分布のようにキレイな分布をしていない場合、最頻値がデータの集団の特徴を表すこともあります。
以下のようなデータを考えてみましょう。
a = np.array([3, 5, 6, 9, 5, 5, 4])
この例では一目で分かりますが、最頻値は5です。NumPyには最頻値を取得する関数が用意されていないので、自分でコードを書く必要があるでしょう(SciPyと呼ばれるNumPyベースのライブラリにはこれを計算するscipy.stats.mode関数があります)。
典型的には次のようなコードがあります。
uniq, idx = np.unique(a, return_counts=True)
print(uniq, idx) # [3 5 6 9] [1 4 1 1]
max_count = np.max(idx)
print(max_count) # 4
print(max_count == idx) # [False True False False]
result = uniq[max_count == idx].tolist()
print(result) # [5]
numpy.unique関数は多次元配列を受け取り、そこから重複する要素を取り除き、要素が昇順に並べられた配列を返します。このときに、return_counts=Trueを指定すると、元の配列で各要素が出現した回数を含む配列も返します(こちらの配列は、同時に返される重複する要素が取り除かれた配列で同じインデックス位置にあるものの出現回数を表すようになっています)。
最初の2行では、この関数を呼び出して、返された配列と出現回数を表示しています。後者の配列では第1要素(0始まり)の値が4であり、これに対応する配列の第1要素が5となっていることに注目してください。
変数max_countには先ほど見たnumpy.max関数で2つ目の配列の最大値を取り出しています。「max_count == idx」というのは、出現回数を含む配列(の各要素)と最大出現数とを比較して、等しければその値がTrueに、そうでなければFalseになるような計算をしています。上の場合は最大出現数が4で、出現回数を格納する配列が[1 4 1 1]なので結果は[False True False False]となります。これをブーリアンインデックスとして、重複要素が取り除かれた配列に適用することで、Trueに対応する5だけを要素として含む配列が得られます。最後のtolist()は配列をリストに変換するものです。
このような手順で最頻値を取り出せることは覚えておきましょう。
分散と標準偏差
これらは平均値に対する、実際のデータのばらけ具合を示す値で、標準偏差(分散)が大きければ大きいほど、平均値に対してデータが実際に存在する範囲が広く(データのばらけ具合が大きく)なります。詳しいことは「分散(Variance)/標準偏差(SD:Standard Deviation)とは?」を参照してください。
NumPyでは分散はnumpy.var関数で、標準偏差はnumpy.std関数で計算できます。
以下に例を示します。
result = np.var(scores, axis=0)
print(result) # [218.05 175.89 76.21 92.76 191.36]
result = np.std(scores, axis=0)
print(result) # [14.76651618 13.26235273 8.7298339 9.6311993 13.83329317]
result = np.mean(scores, axis=0)
print(result) # [55.5 42.9 61.7 38.2 59.8]
print(scores)
# 出力結果:
#[[74 27 64 51 61]
# [58 38 72 33 57]
# [79 28 76 49 54]
# [60 63 58 28 71]
# [55 50 62 41 64]
# [39 54 49 29 53]
# [45 56 50 31 36]
# [29 40 53 25 92]
# [49 51 69 44 51]
# [67 22 64 51 59]]
ここでは分散よりもその平方根を取った標準偏差について見た方が直観的かもしれません。平均値と標準偏差には、その集団に含まれるデータの70%弱は平均値±標準偏差の値の範囲に収まるという関係があります。つまり、各科目のデータの70%弱はその平均点±標準偏差の値の範囲に収まります。例えば、科目Aであれば、平均値は55.5点、標準偏差は14.8ほどです(おおざっぱな話にしています)。よって、55−15=40点くらいから55+15=70点くらいの範囲に多くのデータが含まれているだろうということです。すると、6、7個のデータは確かにこの範囲に収まっています。他の科目についても同様な傾向にあるはずです。
少し駆け足になってしまったような気もしますが、今回紹介した関数やメソッドを使うことで、多数のデータがどのような特徴を持った集団になっているかを調べられることをご理解いただければ十分です。
次回は仮想のデータではなく、実際のデータを使って考察を行ってみるつもりです。
Copyright© Digital Advantage Corp. All Rights Reserved.