調和平均とは？ 算術平均との違い、使い分け：AI・機械学習の用語辞典

用語「調和平均」について説明。データの各数値の逆数で平均を取り、さらにそれを逆数にして戻した値を表す。計算式にすると、データ数を「データの各数値の逆数」の総和で割る形になる。速度／レート（率）のデータ（＝逆数の形で加算される加法的なデータ）を平均する場合に適した平均の計算方法だ。

[一色政彦，デジタルアドバンテージ]

連載目次

用語解説

　最も一般的に使われる「平均」とは、全ての数値を足して合計し、それを数値の総数で割ることである。これは、数学／統計学／機械学習において「算術平均」と呼ばれる。平均には他にも、「加重平均」や「幾何平均」「調和平均」「トリム平均」「移動平均」などがある。本稿ではこれらのうち調和平均について解説する。なお算術平均については、「平均値（Mean）／中央値（Median）／最頻値（Mode）とは？」で説明しているので併せて参照してほしい。

　数学／統計学／機械学習における調和平均（Harmonic Mean）とは、データの各数値の逆数*1で平均を取り、さらにそれを逆数にしたものである。

図1　調和平均のイメージ

　以下では「算術平均と何が違うのか」が分かるように、算術平均と調和平均の計算方法と数学公式を紹介し、最後に使い分け指針をまとめる。計算方法の説明は冒頭の説明の繰り返しになるが、公式の意味を分かりやすくするために記述したので、ご了承いただきたい。

算術平均

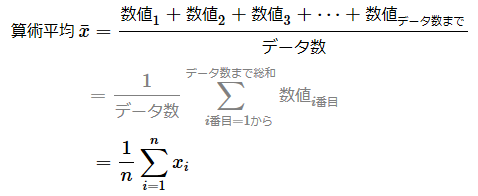
　算術平均（Arithmetic Mean）値とは、データの各数値（x_iは、数値₁, 数値₂, ..., 数値_nのいずれかの数値）を全て足した合計値をデータ数（n）で割った値のことである。算術平均は相加平均とも呼ばれる。数学の公式は以下のようになる。

　算術平均は、最も一般的な「平均」の計算方法で、通常はこれを使えばよい。例えば月ごとの平均気温を求めたり、英語の試験の平均点を求めたりするのに使える。

調和平均

　調和平均（Harmonic Mean）値とは、より分かりやすくシンプルに表現すると、「データ各数値の逆数の平均を、再び逆数にして戻したもの」を意味する。これをより計算しやすくコンパクトに表現すると、データ数（n）を「データの各数値（x_iは、数値₁, 数値₂, ..., 数値_nのいずれかの数値）の逆数（1/x_i）」の総和（Σ）で割った値のことである。なお、データにゼロ（0）や負の値を含めることはできないので注意してほしい（0で割り算はできないし、負の値は計算自体は可能だが意味のある計算結果にならないので）。数学の公式は以下のようになる。

　調和平均は、速度や効率といったレート（率）のデータの平均値を求める場合に、算術平均の代わりに用いるとよい。この場合の“レート（率）”のデータとは、2つの値の比率、つまり、

で表される値である。例えば「速度」は、距離と時間の比率、つまり、

で表される。

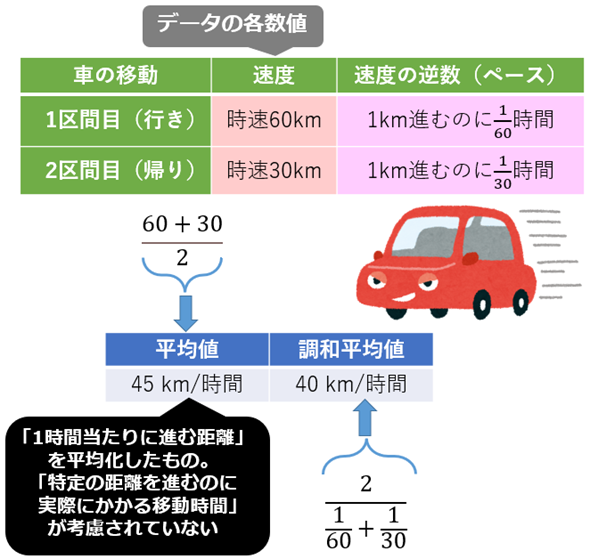
　例えば、ある車が2つの異なる「速度」で、同じ距離である2つの区間を移動（例えば自宅〜会社を往復）した場合を考えてみよう。1区間目（行き）を時速60km（1時間当たり60km）、2区間目（帰り）を時速30km（1時間当たり30km）で走行したとする。このケースで2つの「速度」の平均を取りたい場合、算術平均よりも調和平均がより適切だ。実際にこの数値例で調和平均値を計算してみよう。

（1）逆数（速度→ペース）を計算

　まず、速度（＝1時間当たりに進む距離km）の逆数（＝距離1km進むのにかかる時間、ここでは「ペース」と呼ぶことにする）に注目する。

（2）全ての逆数（ペース）を加算

　次に、計算した全てのデータ（この場合は2つ）の逆数（＝ペース）を加算する。つまり、ペースの合計値が求まる。

（3）全ての逆数（ペース）を平均

　加算した全逆数（＝ペースの合計値）をデータ数（n、この場合は2つ）で割る。これにより、ペースの平均値が求まる。

（4）逆数（ペース→速度）を計算

　最後に、逆数の平均（＝ペースの平均値）の逆数を取る。これにより、ペースの平均値から平均速度が求まる。

　以上の計算結果により、平均速度（＝1時間当たりに進む平均距離km）は40km/時間と求まった。

　このように調和平均は「逆数の平均の逆数」を計算することで求まり、その計算式は前述の公式のようにまとめることが可能だ。

　ちなみに単純な算術平均を用いると、時速60kmと時速30kmの平均速度は（60＋30）÷2＝45km/時間となるが、この計算は単に「1時間当たりに進む距離」を平均化したものであり、「実際に特定の距離を進んだ際の平均時速」とは異なる値になる。例えば、往路の60kmを時速60kmで走り、復路の60kmを時速30kmで走る場合、全体でかかる時間は3時間である。この場合、総移動距離120kmをかかった時間3時間で割ると、平均速度は120÷3＝40km/時間となり、これは調和平均の値と一致する。従って、「特定の距離を進むのに実際にかかる移動時間」を考慮して平均速度を求める場合は、調和平均を用いるのが適切だ。

　「速度」や「効率」の平均以外にも調和平均は、統計学／機械学習で使われる評価指標のF値（F-measure）／Fスコア（F-score）の計算にも使われている（詳しくは左記のリンク先を参照してほしい）。

算術平均と幾何平均と調和平均の使い分け指針

　「どういう場合にどちらの平均を採用すればよいか」は既に説明したが、以下に使い分け指針をまとめておく。

• 各数値が同じ重要度を持つデータを平均したい場合　→　算術平均（相加平均）
• 時間に応じて変化する変化率／比率／倍率のデータ（＝乗算後に累積される乗法的なデータ）を平均したい場合　→　幾何平均（相乗平均）
• 速度／レート（率）のデータ（＝逆数の形で加算される加法的なデータ）を平均したい場合　→　調和平均

　これら3つの平均の間には、

　　「算術平均（相加平均）≧ 幾何平均（相乗平均）≧ 調和平均」

という関係が成り立つ。この数学的な特性も、適切な平均値を選択する際の重要な指針となる。

「AI・機械学習の用語辞典」