[NumPy超入門]相関係数とヒートマップ、散布図を使ってデータセットをさらに可視化してみよう:Pythonデータ処理入門(2/2 ページ)
2種類のデータの関連の度合いを調べるには相関係数やそれを可視化したヒートマップ、散布図を使ってデータセットの調査をさらに進めていきましょう。
散布図を使って2つの列に相関があることを確認しよう
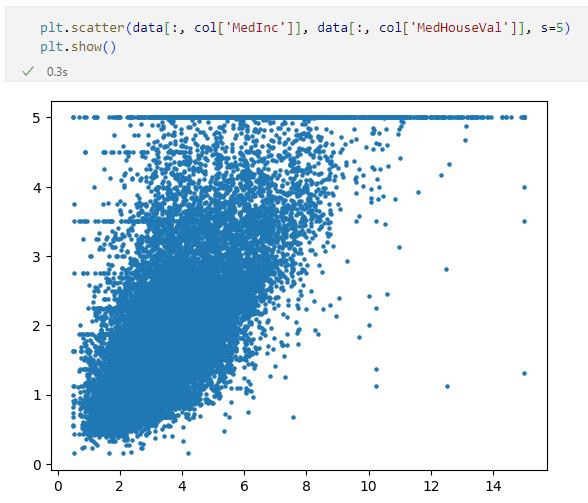
ということで、次にそれなりの相関がありそうだった'MedInc'列と'MedHouseVal'列が正の相関を持っているかどうか、'MedInc'列の値をX軸に、'MedHouseVal'列の値をY軸に取って散布図を作成してみます。
これにはMatplotlibが提供するscatter関数にX軸の値となるデータとY軸の値となるデータを渡すだけです。以下にコードを示します(以下で指定しているもう1つのsパラメーターはドットのサイズを指定するものです)。
plt.scatter(data[:, col['MedInc']], data[:, col['MedHouseVal']], s=5)
plt.show()
結果は次のようになります。
確かに全体としては右肩上がりのグラフになっているので、正の相関がありそうです。しかし、Y軸の一番上に多くのドットがへばり付いているのが気になります。これは「どんな地区であっても高額な住宅が存在する」ことを示しているのではないでしょうか。
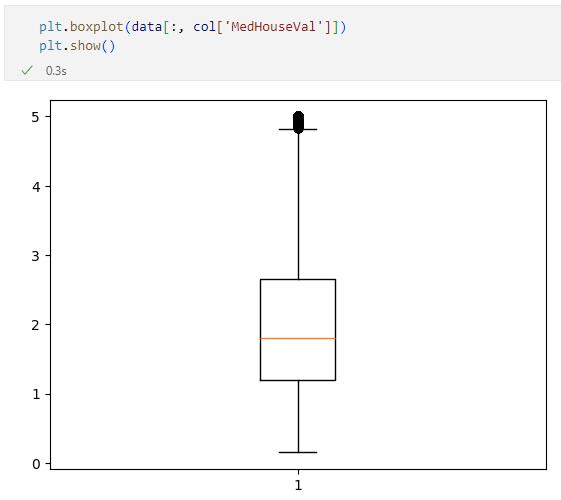
'MedHouseVal'列の値を箱ひげ図を用いて可視化すると次のようになります。
高額所得者とは無関係なおおよその傾向を調べるのであれば、この画像で上限(一番上の水平線)よりも上の値は外れ値としてデータセットから取り除いた方がよいかもしれません。
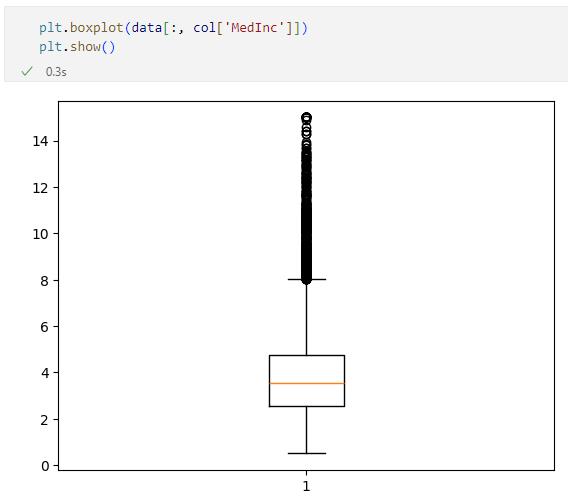
同様に、'MedInc'列についても箱ひげ図を用いて可視化してみましょう。
こちらは、上限(四分位範囲の1.5倍を第3四分位数に加算した値)よりも上にある値がさらに多くなっています。全てを外れ値とすべきかどうかは微妙かもしれませんが、どこかで線を引いて、それよりも上の値は外れ値としてデータセットからは取り除くことを考えてもよいでしょう。
numpy.where関数
このようなときに便利なのが、NumPyのnumpy.where関数です。
numpy.where(condition[, x, y])
この関数はconditionパラメーターに指定した条件がTrueとなる値についてはxパラメーターに指定した値を、そうでなければyパラメーターに指定した値を返します。ですが、これらは省略可能で、conditionパラメーターに条件だけを指定することも可能です。その場合、ドキュメントによれば、この関数はnumpy.asarray関数に条件を指定して呼び出した結果を基に、今度はnumpy.nonzero関数を使って、その条件を満たした要素のインデックスだけを返すといった処理を行います。といっても分かりにくいので、少し実験しましょう。
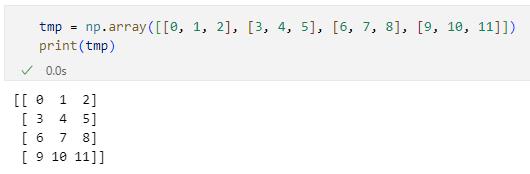
tmp = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 10, 11]])
print(tmp)
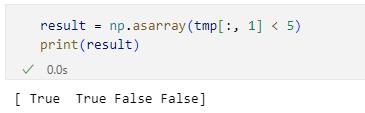
result = np.asarray(tmp[:, 1] < 5)
print(result)
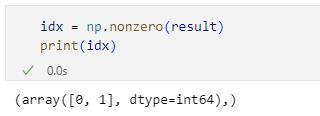
idx = np.nonzero(result)
print(idx)
tmp[idx]
このコードではまず4行3列の二次元配列を作成しています。
ここまでは特に難しくはありません。次の「result = np.asarray(tmp[:, 1] < 5)」行では、numpy.asarray関数に「tmp[:, 1] < 5」という条件を渡しています。これは第1列の値が5未満を意味しているので、この条件を満たすのは第0行と第1行です。この結果、第0要素と第1要素がTrueで、残りがFalseとなる配列が返されます。
このように、最初の2つの要素がTrue、残りがFalseという配列が得られました。最後に、これをnumpy.nonzero関数に渡すとnumpy.asarray関数から得た配列で要素が0以外(つまり、True)のもののインデックスが返されます。
この配列を元の配列tmpのインデックスとして指定することで(これは第4回で紹介しているファンシーインデクシングです)、条件を満たす行だけが取得できるというわけです(numpy.nonzero関数がタプルを返送しているので、ここではその先頭要素を取り出すようにしている点には注意してください)。
これをnumpy.where関数を用いたコードに書き直すと次のようになります。
tmp = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 10, 11]])
print(tmp)
idx = np.where(tmp[:, 1] < 5)[0]
print(idx)
tmp[idx]
これを実行すると、上と同様に条件(第1列の値が5未満)を満たす行だけが得られます。
外れ値の除去
では、元のデータセットから外れ値を除去してみましょう。除去するということは、条件に満たす要素だけからなる配列を新たに作成するということに注意してください。ここでは以下の条件を満たさないものを外れ値とします。
- 'MedInc'列の値が10未満
- 'MedHouseVal'列の値が5未満
なお、numpy.where関数には複数の条件も記述できます。そのときには「numpy.where((条件1) & (条件2))」のように記述します。というわけで、以下にコードを示します。
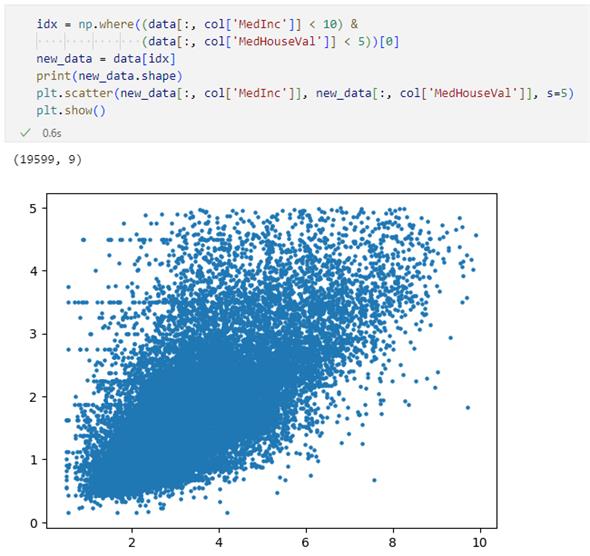
idx = np.where((data[:, col['MedInc']] < 10) &
(data[:, col['MedHouseVal']] < 5))[0]
new_data = data[idx]
print(new_data.shape)
ここでは条件を満たす行だけからなる配列を変数new_dataに代入するようにしました(結果的に外れ値が除去されます)。また、最後の行ではその形状を表示しています(もともとは2万行を超えるデータがありました)。
後は、新しいデータセットの'MedInc'列と'MedHouseVal'列の値から散布図を作成するだけです。
plt.scatter(new_data[:, col['MedInc']], new_data[:, col['MedHouseVal']], s=5)
plt.show()
すると、次のような結果が得られます。
どうでしょうか。おおよその傾向を調べるのであれば、こちらの方がよさげではありませんか。最後に冒頭で紹介したコードと同様なコードでヒートマップを作成してみます。
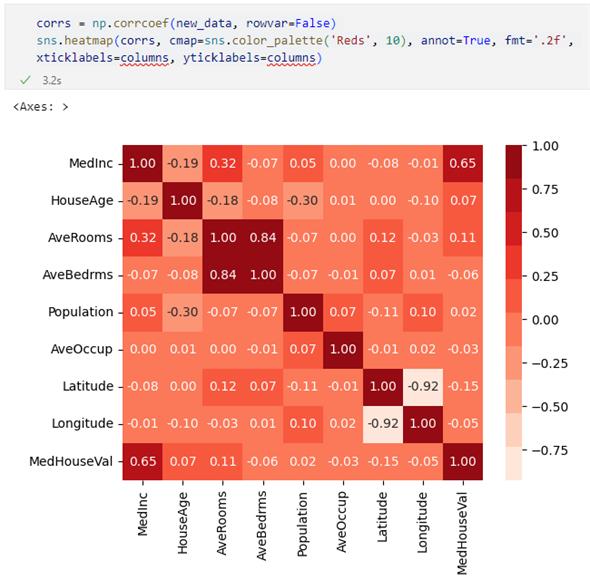
corrs = np.corrcoef(new_data, rowvar=False)
sns.heatmap(corrs, cmap=sns.color_palette('Reds', 10), annot=True,
fmt='.2f', xticklabels=columns, yticklabels=columns)
実行結果を以下に示します。
次回に続く
ところで、カリフォルニア州の住宅価格データセットは、カリフォルニア州を多数の地区に分けて、それらの地区の平均の所得や部屋数、寝室数などから住宅価格を予測するためのものでした。上のデータを基にそうした予測は可能なのでしょうか。次回は単回帰分析と呼ばれる手法でこれを試してみることにしましょう。
そのため、以下のコードで今回作成した新しいデータセットを保存しておきましょう。
np.savetxt('new_data.csv', data, header=','.join(columns), delimiter=',')
Copyright© Digital Advantage Corp. All Rights Reserved.