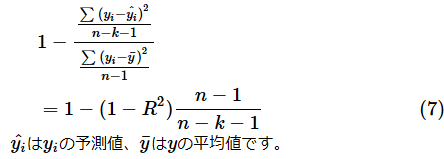[データ分析]重回帰分析による予測(線形回帰、多項式回帰) 〜 年式、走行距離、排気量から中古車の価格を予測:やさしいデータ分析
データ分析の初歩からステップアップしながら学んでいく連載の第15回。複数の説明変数を基に目的変数の値を予測する重回帰分析について、Excelを使って手を動かしながら学んでいきましょう。カテゴリーなどの数値ではないデータを説明変数として利用する方法や、二次関数などの多項式を基に回帰分析する方法も紹介します。
連載:
この連載では、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学びます。
データの収集方法、データの取り扱い、分析の手法などについての考え方を具体例で説明するとともに、身近に使える表計算ソフト(ExcelやGoogleスプレッドシート)を利用した作成例を紹介します。
必要に応じて、Pythonのプログラムや統計ソフトRなどでの作成例にも触れることにします。
数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く99回で一旦中断。さらにリターンライダーを目指し、大型二輪免許を取得。1年かけてコツコツと貯金し、ようやくバイクを購入(またもや金欠)。
前回は単回帰分析により、説明変数xの値から目的変数yの値を予測するための回帰式を求めたり、回帰式を基に予測を行ったりしました。
今回は、説明変数が複数ある場合の重回帰分析に取り組みます。図1の例であれば、年式が説明変数x1、走行距離が説明変数x2、排気量が説明変数x3となり、本体価格が目的変数yとなります。図1のデータでは実際のメーカーや車種の名称が使われていますが、本体価格などの値は架空のものです。
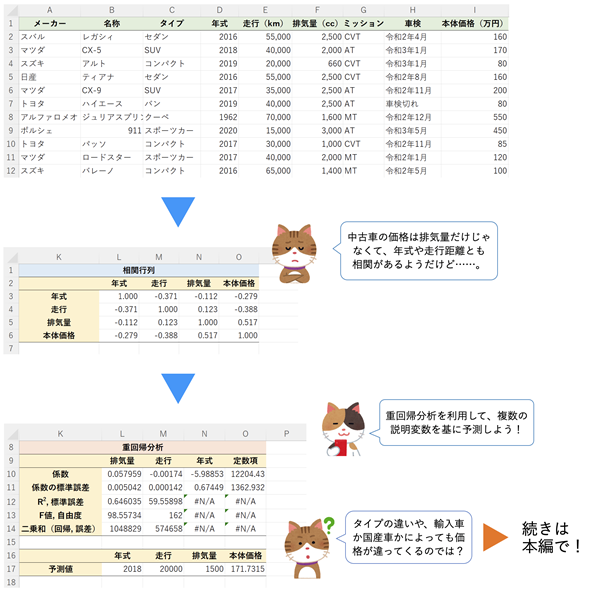
図1 重回帰分析を利用して中古車の価格を予測する
中古車のデータを基に各項目同士の相関係数を求めてみると、年式と本体価格、走行距離と本体価格では負の相関があり、排気量と本体価格には正の相関があることが分かる。つまり、年式、走行距離、排気量という複数の説明変数を利用すれば、単回帰分析よりも本体価格がよく予測できそうである。そのための重回帰分析について考え方と操作の手順を追いかけよう。タイプの違いや、輸入車かどうかといった名義尺度のデータを重回帰分析で利用するための方法についても見ていく。
図1のデータは、前回のデータと同じものです。このデータを使って重回帰分析を行います。簡単な関数を利用するだけでできますが、説明変数の範囲がやや複雑になるので、「名前」機能などを使って、引数を簡単に指定できるようにします。
年式と本体価格に負の相関がある(年式が大きくなれば価格が下がる=新しい車ほど安い)という結果には違和感がありますね。これには理由があります。前回は排気量に注目して電気自動車(EV)を除外し、本体価格に注目して極端に高価な中古車を外れ値として除外しましたが、年式にも外れ値があるということです(例えば、8行目のアルファロメオは1962年式ですね)。このことについては、後ほど触れるので、取りあえずこのまま重回帰分析を進めましょう。
最後に、二次式以上の回帰式を利用した多項式回帰の例についても紹介します。具体的には、第13回で取り上げた、気温と電気器具によるCO2排出量のデータのようなU字形の分布について回帰分析を行います。重回帰分析のちょっとした応用で簡単にできます。
この記事は、データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の第15回です。第13回から第15回までは「関係」に注目し、相関や回帰分析などについて見ていきます。前回は、1つの説明変数から目的変数の値を予測する単回帰分析を紹介しました。今回は、複数の説明変数から目的変数の値を予測する重回帰分析の考え方や取り扱いを見ていきます。また、回帰式が二次以上の式になる多項式回帰にも取り組みます。トップページから全体の目次が参照できます。記事冒頭のボタンからぜひメール通知にご登録ください。
この記事で学べること
今回は以下のようなポイントについて、分析の方法や目の付けどころを見ていきます。
- 重回帰分析による回帰式の求め方 …… 重回帰式の係数と定数項を求める
- 重回帰分析による予測 …… 回帰式に値を代入して予測を行う
- 名義尺度のデータを説明変数にする方法 …… カテゴリー変数を数値化する
- 重回帰分析での留意点を知る …… 多重共線性の意味と確認の方法
- 多項式回帰についても理解する …… 二次関数のような直線的でない関係でも回帰分析を行う
今回は、変数同士の相関係数を全て求めるところからスタートします。サンプルファイルの利用についての説明の後、本編に進みましょう。
サンプルファイルの利用について
本稿では、表計算ソフトを使って手を動かしながら学んでいきます。表計算ソフトMicrosoft Excel用の.xlsxファイルをダウンロードできるようにしています。デスクトップ版のExcelが手元にない場合は、Microsoftアカウントで使える無料のMicrosoft 365オンライン、もしくはGoogleアカウントで使える無料のGoogleスプレッドシート(Google Sheets)をお使いください。Microsoft 365オンラインの場合は、.xlsxファイルをOneDriveにアップロードしてから開いてください。Googleスプレッドシートの場合は、ファイルを共有して参照できるようにします。リンクを開き、メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
相関行列を作成しよう 〜 説明変数を選定する
今回の例では、年式、走行距離、排気量を説明変数とすることにしていますが、本来はどの項目(変数)を説明変数とするかを選定する必要があります。そのためには、目的変数と何らかの関係がある項目を選ぶ必要があります。変数同士の関係を知るには相関係数を求めたり、散布図を描くというのが定石ですね。そこで、それぞれの相関係数を求めてみましょう。
といっても、幾つかのCORREL関数にいちいち異なる範囲を指定するのはとても面倒です。そこで、図2では、範囲に名前を付けて関数を入力しやすくしています。ただし、ブック全体で同じ名前を使っているので、以下の操作については既に設定済みとなっています(つまり、後述するサンプルファイルでは図2の操作は必要ないので、操作方法の確認だけしておいてください)。
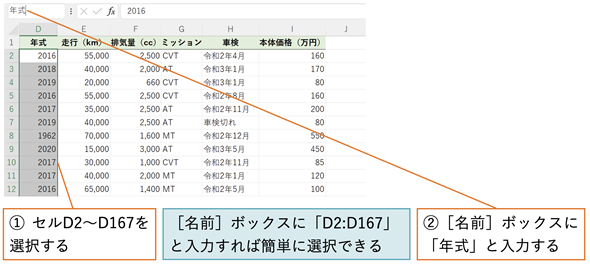
図2 数式を簡単にするためにあらかじめ範囲に名前を付けておく
[数式]タブで[名前の定義]を選択すれば、範囲に名前を付けておくことができる。数式の中では、範囲指定の代わりにここで付けた名前が使える。ここでは、年式という名前をブック全体で使える名前として、セルD2〜D167に付けている。走行、排気量、本体価格についても同様に名前を付けておくとよい。
サンプルファイルをこちらからダウンロードして[中古車価格]ワークシートを開いてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
実際の作業は不要ですが、事前に設定した際の手順は以下の通りです。データは167行目まで入力されています。
- [名前]ボックスに「D2:D167」と入力してセルD2〜D167を選択する
- セルD2をクリックしてから[Ctrl]+[Shift]+[↓]キーを押してもセルD2〜D167が選択できる
- [名前]ボックスに「年式」と入力する
同じ手順で走行という名前をセルE2〜E167に、排気量という名前をセルF2〜F167に、本体価格という名前をセルI6〜I167に付けてあります。このようにして、範囲に名前を付けておくと、数式や関数の引数としてセルアドレスを指定する代わりに名前が使えるようになります。
Excelでは、年式については、セルD1〜D167を選択し、[数式]タブの[定義された名前]グループにある[選択範囲から作成]ボタンをクリックし、[選択範囲から名前を作成]ダイアログボックスで[以下に含まれる範囲から名前を作成]の[上端行]をチェックしても作成できます。上端行が名前となり、その下の範囲が名前で表される範囲となります。
なお、ブック全体ではなく、特定のワークシートで使われる名前にするには[数式]タブの[定義された名前]グループにある[名前の定義]ボタンをクリックし、[新しい名前]ダイアログボックスで、[範囲]のリストからワークシート名を選択して、名前と範囲を指定します。
続いて、図3でCORREL関数を入力します。ここから実際の操作に入るので、サンプルファイルの[中古車価格]ワークシートを開き、図の後に記した箇条書きの手順に従って取り組んでみてください。また、ここから重回帰分析の結果までの作成例は[中古車価格(作成例)]ワークシートに含まれています。
図2と図3の手順については動画も用意してあります。操作方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。
動画1 Excelで重回帰分析(線形回帰)の回帰式を可視化/計算するには
では、CORREL関数を入力しましょう。手順は図3に示した通りです。名前機能を使えば、数式が簡潔に入力できることが分かりますね。
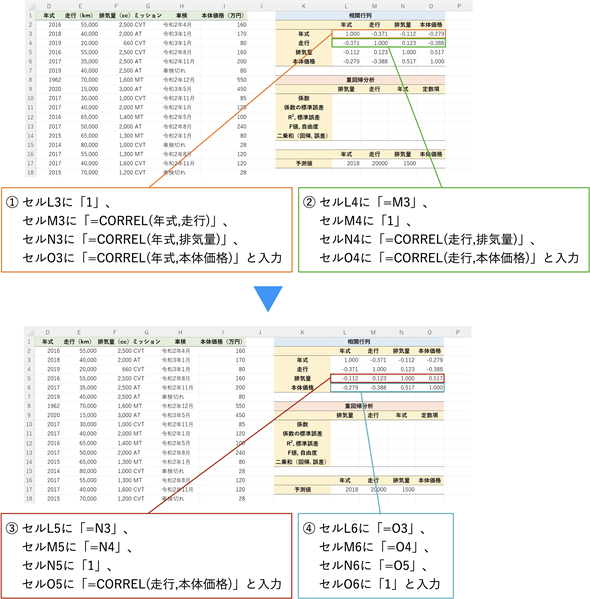
図3 CORREL関数を利用して相関行列を作成する
自分自身との相関係数は1なので、表の対角線の位置(セルL3、M4、N5、O6)には単に「1」と入力するだけで構わない。セルM4には=CORREL(年式,走行)と入力する。対角線を挟んで対称の位置にある値は同じ。例えば、セルL4には=M3と入力するだけでよい。
手順は図中に示した通りですが、以下に箇条書きにしておきます。
- 3行目
- セルL3: 1
- セルM3: =CORREL(年式,走行)
- セルN3: =CORREL(年式,排気量)
- セルO3: =CORREL(年式,本体価格)
- 4行目
- セルL4: =M3
- セルM4: 1
- セルN4: =CORREL(走行,排気量)
- セルO4: =CORREL(走行,本体価格)
- 5行目
- セルL5: =N3
- セルM5: =N4
- セルN5: 1
- セルO5: =CORREL(排気量,本体価格)
- 6行目
- セルL6: =O3
- セルM6: =O4
- セルN6: =O5
- セルO6: 1
実は、文字列をセル参照に変換するためのINDIRECT関数を使うと、もっと簡単に相関行列が作成できます。手順はセルL3に=CORREL(INDIRECT($K3), INDIRECT(L$2))と入力し、セルO6までコピーするだけです。
INDIRECT関数を使いこなすには、文字列とセル参照の違いを明確に理解しておく必要があります。例えば、「"A4"」という文字列は、単に「"A"」という文字と「"4"」という文字が並んだだけのデータですが、A4というセル参照はセルA4を指し示すものです。例えば、INDIRECT("A4")とすると、「"A4"」という文字列がセル参照A4に変換されます。
=CORREL(INDIRECT($K3), INDIRECT(L$2))であれば、セルK3に入力されている「"年式"」という文字列がINDIRECT関数によって年式という名前(セル参照)に変換されます。同様に、セルL2に入力されている「"年式"」という文字列もやはり年式という名前に変換されます。従って、この式は=CORREL(年式,年式)と入力したのと同じことになります。その式を右のセルM3にコピーすると、引数のL$2の列番号だけが変わりM$2になるので、関数は=CORREL(INDIRECT($K3), INDIRECT(M$2))となります。セルM2に入力されている「"走行"」という文字列がINDIRECT関数によって走行という名前に変換されるので、=CORREL(年式,走行)と入力したのと同じことになります。このようにして、セルO6までの全ての値が求められます。
INDIRECT関数はちょっと難しいですが、サンプルファイルの[INDIRECT関数の利用例]ワークシートに幾つか例を掲載しているので、参考にしてください。ただし、INDIRECT関数が分かりにくいという方や、INDIRECT関数を使うとそのワークシートを使う他の人が理解できないかもしれないという懸念のある方は、図3の手順で示したように入力した方がいいかと思われます。
相関行列のお話が長くなりましたが、これで目的変数と関係のありそうな説明変数の候補が選定できます。
コラム 全ての変数の組み合わせについて散布図を描くには
説明変数を選択したり、外れ値の除外を行ったりするために、それぞれの散布図を描いて変数同士の関係を可視化したいところですが、Excelではかなり面倒です(操作そのものは簡単ですが、組み合わせが多いので1つずつ散布図を描いていくのは手間が掛かります)。そこで、Pythonのプログラムを書いて、全ての組み合わせについて散布図を描いてみます。
連載の第12回で紹介したseabornモジュールのpairplot関数を使えば簡単です。サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryで以下(リスト1)のコードが表示されます(Googleアカウントでのログインが必要です)。
!pip install japanize-matplotlib # グラフに日本語を表示するために必要。最初に1回だけ実行すればよい
import pandas as pd
import japanize_matplotlib
import seaborn as sns
df = pd.read_excel("https://github.com/Gessys/data_analysis/raw/main/15a.xlsx",
sheet_name="中古車価格", usecols="A:I")
sns.pairplot(df)
seabornモジュールのpairplot関数を使えば、全ての変数同士の散布図が描かれる。同じ変数同士(対角線上の部分)についてはヒストグラムが描かれる。
実行結果は図4の通りです。外れ値や分布の歪み、変数同士の関係が可視化できるので、前処理やモデルの選択などに役立てることができます。
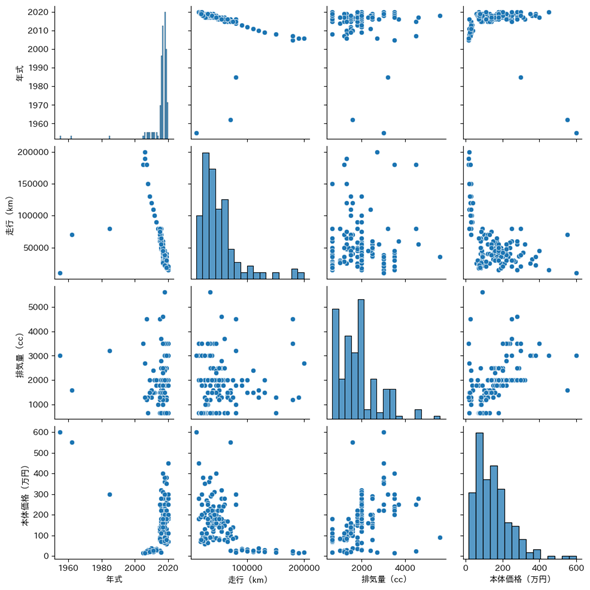
図4 変数同士の組み合わせ全てについて散布図を描く
散布図を見ると、年式が極端に古い中古車が3つあることや、排気量が5000ccを超える特殊な車両があることも分かる。それらを除外すれば、年式と本体価格が直線的な関係になりそうである(このことについては、後のコラムで少し触れる)。走行距離については、10万kmを超えると本体価格がほとんど下限に近くなることが分かる。さらに、ヒストグラムを見れば、排気量が小さい中古車(軽自動車)が多いことも分かる。軽自動車を別扱いにすることも考えられるが、今回はこのまま進めることとする。
重回帰分析を行う 〜 重回帰式の係数と定数項を求める
では、重回帰分析に取り組みましょう。重回帰分析では、説明変数が複数あるので、回帰式は以下のように表されます。
前回は、中学で学んだ一次関数y=ax+bと同じように単回帰式の定数項を最後に書きましたが、回帰分析では定数項を前に書くのが一般的です。(1)式ではa0が定数項です。係数や変数が複数個あり、a, b, c, ...のようなアルファベットを使っているとかえって煩雑になるので、a0, a1, ...、x1, x2 ...のように添え字を付けて区別します。
単回帰分析は、データの近くを通る(実測値と予測値の差の二乗和が最小になる)直線を描くイメージでしたが、説明変数が2つの重回帰分析は、データの近くを通る平面を描くイメージです。説明変数が3つ以上になると、さらに次元が増えるので図として表すのが難しくなりますが、同様にデータの近くを通る「超平面」を描くようなイメージです。(1)式にはx0の項が書かれていませんが、最初の項がa0x0であり、x0=1であるものと考えられます。
中古車のデータでは、本体価格が目的変数yに当たり、年式が説明変数x1に、走行距離が説明変数x2に、排気量が説明変数x3に当たります。具体的に書けば、以下のようになりますね。
というわけで、説明変数と目的変数を基に、それぞれの係数と定数項を求めてみましょう。そのためにはLINEST関数を使います。以下の例では補正項と呼ばれる値も求めてみます。補正項は、重回帰式の当てはまりの良さや係数の有効性についての検定を行うのに使われます。
手順は図5の後に記した通りです。セルL10に=LINEST(I2:I167,D2:F167,TRUE,TRUE)と入力しましょう。ただし、スピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルL10〜O14)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押してください。以降、この操作を「配列数式を入力する」と呼ぶことにします。
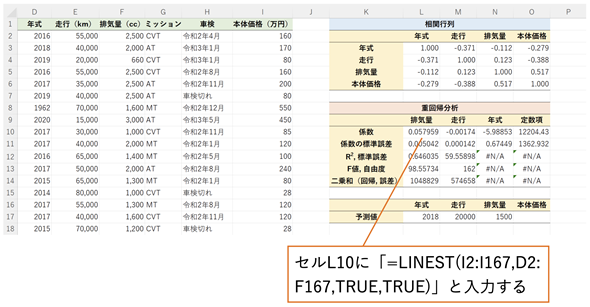
図5 重回帰分析により係数や定数項を求める
目的変数の値はセルI2:I167に入力されている、説明変数の値はセルD2:F167に入力されている。
第3引数には定数項を求めるか、定数項を0とするかを指定する。ここではTRUEを指定して定数項を求める。
最後の引数には補正項を求めるかどうかを指定する。ここではTRUEを指定して補正項も求める。係数と定数項だけを求めるのであれば、FALSEでも構わない。
LINEST関数だけで全ての値が求められるが、係数が元の項目と逆の順序(排気量、走行、年式)になることに注意。
図5の解説にも記してありますが、求められた係数は元の項目と逆の順序になっていることに注意してください。得られた値を(2)の回帰式に当てはめると、以下のようになります。
セルL11〜O14の値が補正項です。これらの補正項を使った検定については、この連載の次に企画している推測統計編で取り扱うことになるので、これ以上は触れませんが、セルL12の値(R2:決定係数)とセルM12の値(SE:標準誤差)は、重回帰式の当てはまりの良さを評価するのに使われるので、少しばかり気にしておいてください(決定係数は後でまた登場します)。
SE(標準誤差)はRMSE(二乗平均平方根誤差)と似ていますが、SEは、実測値と予測値の差の二乗和(セルM14の値)を自由度(セルM13の値)で割ってその√を求めたもので、RMSEは実測値と予測値の差の二乗和をデータの個数(この例では166)で割ってその√を求めたものです。なお、セルM13の自由度は回帰分析での検定に使われる標準誤差の自由度で、データの個数−説明変数の個数−1で求められます(この例なら166−3−1=162)。
説明変数として利用している年式や走行距離、排気量は値の大きさが異なるので、元の値を使って重回帰分析を行っても、係数の大きさをそのままでは比較できません。係数の大きさを比較できるようにするには、元の値を標準化したものを説明変数とするとよいでしょう。
標準化の方法はこの連載の第6回で紹介した通り、元の値から平均値を引き、標準偏差で割るだけです(STANDARDIZE関数を使ってもできます)。標準化を行うと、全体の平均が0、標準偏差が1となるように値が調整されます。
予測に使う値についても、元の値ではなく、標準化した値を指定します。サンプルファイルの[(参考)標準化]ワークシートにその例を含めてあるのでご参照ください。
重回帰分析による予測を行う
前項で見た(2)式に年式と走行距離、排気量を代入すれば本体価格が予測できます。(2)式は以下の通りでしたね(再掲)。係数と定数項はセルL10〜N10で求められています。
例えば、セルL17〜N17に入力されている年式、走行距離、排気量を基に本体価格を予測するなら、=O10+N10*L17+M10*M17+L10*N17と入力すれば、171.7315という結果が得られます(セルO18などの空いているセルに入力してみてください)。しかし、係数や定数項を求めずに、予測値だけを求めたいのであれば、TREND関数を使うのが簡単です。セルO17に=TREND(I2:I167,D2:F167,L17:N17,TRUE)と入力しましょう(図6)。

図6 重回帰分析による予測を行う
TREND関数には、既知の目的変数yと既知の説明変数x、予測に使う新しいxの値を指定する。
最後の引数は定数項を求めるか、0と見なすかの指定。TRUEを指定すれば定数項を求めることになる。
2018年式で走行距離20000km、排気量が1500ccの中古車の価格は171.7315万円と予測できました。取りあえず、これで重回帰分析による係数と定数項の計算、予測の方法については一通り見たことになります。
ここからは、重回帰分析の精度を評価し、より良い予測ができるようにする方法について見ていきましょう。精度を評価するための決定係数やRMSEについては前回の単回帰分析でも簡単に紹介しましたが、今回はそれらに加えて自由度調整済み決定係数の求め方も説明します。
重回帰分析の精度を可視化/評価する
重回帰分析によって求めた回帰式の当てはまりの良さを可視化するには、
のが最も簡単です。サンプルファイルの[中古車価格(散布図)]ワークシートをご覧ください。I列の本体価格と、J列で求めた予測値を散布図にし、決定係数(R2値)も併せて表示します。手順は図7の後に箇条書きで記してあります。
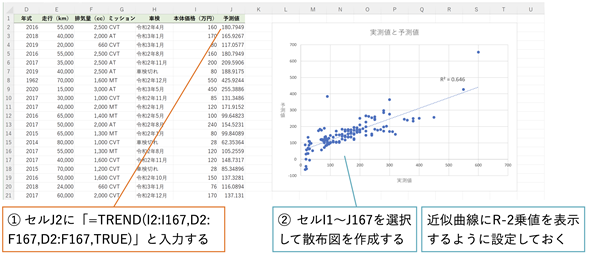
図7 回帰式に当てはまりの良さを可視化する
実測値と予測値の散布図が直線的になれば、回帰式の当てはまりが良いと考えられる。決定係数(R2)はLINEST関数の補正項でも求められているが、散布図の近似曲線に表示することもできる。
手順は以下の通りです。散布図の位置やサイズ、書式の設定などについては省略しています。
散布図の作成(Excelでの操作手順)
- セルJ2に=TREND(I2:I167,D2:F167,D2:F167,TRUE)と入力する(予測値が全て求められる)
- スピル機能が使えない場合は配列数式として入力してもいいが、セルJ2に=TREND(I2:I167,D2:F167,D2:F2,TRUE)と入力してセルJ167までコピーする方が簡単
- セルH1〜I167を選択する
- [挿入]タブを開き、[散布図(X, Y)またはバブルチャートの挿入]ボタンをクリックする
- [散布図]を選択する(これで散布図が作成される)
- 系列(作成された散布図のいずれかの点)を右クリックし、[近似曲線の追加]を選択する
- [近似曲線の書式設定]作業ウィンドウで[グラフにR-2乗値を表示する]チェックボックスをオンにする
散布図の作成(Googleスプレッドシートでの操作手順)
- セルJ2に=ARRAYFORMULA(TREND(I2:I167,D2:F167,D2:F167,TRUE))と入力する(予測値が全て求められる)
- セルH1〜I167を選択する
- メニューバーから[挿入]−[グラフ]を選択する
- [グラフエディタ]作業ウインドウで[グラフの種類]リストから[散布図]を選択する(これで散布図が作成される)
- [グラフエディタ]作業ウインドウで[カスタマイズ]をクリックする
- [系列]をクリックして下位の設定項目を表示し、[トレンドライン]チェックボックスをオンにする
- [系列]の下の[決定係数を表示する]チェックボックスをオンにする
図7を見ると、回帰式の当てはまりは比較的良いように思われます。決定係数は0.646となっていますが、一般に0.5以上あれば当てはまりが良いと考えられます。
ここでは予測値を全てTREND関数で求めているので、毎回、係数と定数項の計算が行われます。従って、係数と定数項が既に求められているのであれば、回帰式に従って予測値を求めた方が速く計算できます。といっても、この程度の規模であれば計算の速さはそれほど変わりません。
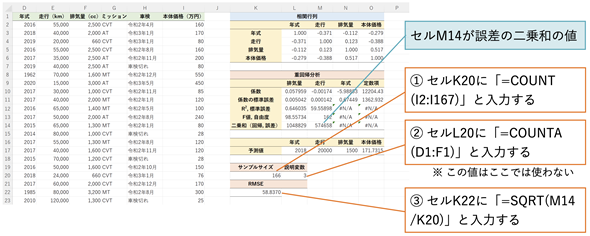
決定係数に加えて、RMSE(二乗平均平方根誤差)も求めておきましょう。RMSEを求めるための式は以下の通りでしたね。
yiはI列の値です。
はyの予測値なのでJ列の値に当たりますね。nはサンプルサイズ(データ数)です。従って、図7の表を基にこの式に従ってRMSEが計算できます……が、実は(4)式の一部の、
はLINEST関数の補正項で既に求められています(誤差の二乗和あるいは残差平方和などと呼ばれます)。というわけで、[中古車価格]ワークシートに戻って計算してみましょう(図8)。
手順は図8に示した通りです。以下のように入力しましょう。
セルL20で求めている説明変数の個数はここでは使いません。次のコラムで使うので、ついでに求めておいただけです。
コラム 決定係数に関する留意点 〜 自由度調整済み決定係数などのお話
一般に、決定係数は説明変数の数が多くなると値が大きくなります。そのため、説明変数の数が多い場合には、説明変数の数を考慮した自由度調整済み決定係数が使われます。自由度調整済み決定係数は以下の式で求められます。詳細については、こちらなどをご参照ください。
決定係数 R2
自由度調整済み決定係数 adj R2
nはサンプルサイズ(データの件数)、kは説明変数の個数を表します。例えば、セルL12に決定係数が求められており、セルK20にデータの件数が、セルL20に説明変数の個数が求められているのであれば、セルK25に=1-(1-L12)*(K20-1)/(K20-L20-1)と入力すれば、自由度調整済み決定係数が求められます(結果は0.6395となります)。[中古車価格(重回帰)]サンプルファイルには(7)式によって計算した結果も含めてあるので、参照してみてください。
ちなみに、(6)式の分母は全変動の二乗和と呼ばれます。この値は回帰変動の二乗和と誤差の二乗和(図8のセルL14とセルM14の和)となっています。分子は誤差の二乗和ですね、従って、空いているセルに「=1-M14/(L14+M14)」と入力しても決定係数が求められます。同様に、自由度調整済み決定係数は「=1-(M14/(K20-L20-1))/((L14+M14)/(K20-1))」でも求められます。
注意点:決定係数が大きいから当てはまりがよいとは限らない?!
もう一点、補足です。元のデータではRMSEが58.8370となっており、決定係数は0.646035となっています。さらに分析の精度を上げるために、年式が極端に古い中古車と排気量が5000ccを超える特殊な車両を除外すると、RMSEは52.0031と小さくなるのですが、決定係数も0.643666とわずかに小さくなってしまいます(サンプルファイルの[参考(外れ値の除外)]ワークシートに計算例があります)。
誤差が小さくなったのに、決定係数で表される回帰式の当てはまりは悪くなったということでしょうか。実は、これは決定係数を求めるための(6)式で分母(全変動の二乗和)が分子(回帰の変動の二乗和)に比べて小さくなったためです。従って、決定係数が大きいからといって当てはまりがよいとか、決定係数が小さいから当てはまりが悪いと直ちには言えない場合もあることに注意が必要です。このことについては、こちらに詳しい解説があります。
特徴量を作成する
ここまでは、中古車の価格が年式、走行距離、排気量といった値で決まるものとして分析を進めてきました。しかし、輸入車であるか国産車であるかによっても中古車の価格が異なることは十分考えられます(一般に輸入車の方が高価だと考えられますね)。このように、元々のデータには存在しなかった項目(特徴量)を新たに追加することによって、分析の精度を向上させることができる可能性もあります。
では、輸入車であるか、国産車であるかをどのようにして数値で表せばいいでしょうか。輸入車か国産車かというように、2つのカテゴリーに分けられる場合は、輸入車を1とし、国産車を0とする方法が使えます。回帰式の中での、その項をaixiとすると、輸入車の場合、その項の値はai × 1=aiとなり、国産車の場合はai × 0 = 0となりますね。輸入車にはaiだけ価格が上乗せされるというわけです。
サンプルファイルの[中古車価格(特徴量)]ワークシートを使って手順を追いかけてみましょう。ここからの手順については動画も用意してあります。操作方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。
動画2 Excelで重回帰分析のための特徴量を作成するには
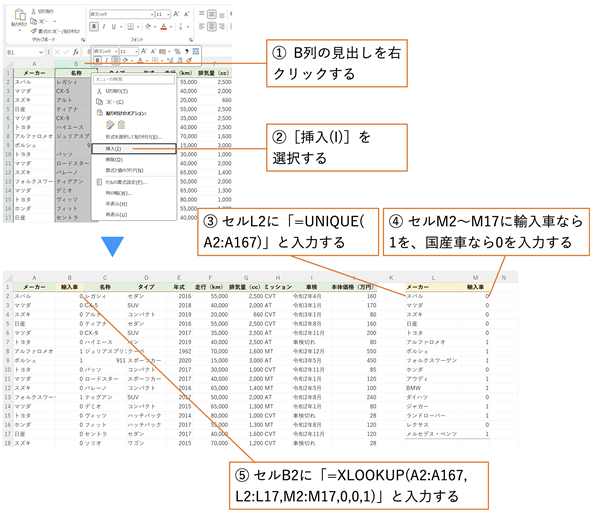
まず、輸入車であるかどうかを表す項目を作成しましょう(図9)。UNIQUE関数を使ってメーカーの一覧を作成し、輸入車であれば1を、国産車であれば0を入力した表を作ります。次に、XLOOKUP関数を使ってそれぞれの中古車が輸入車であるか国産車であるかをB列に表示されるようにします。
Excel 2019以前のバージョンでは、以下の手順に登場するUNIQUE関数が使用できません。それらのバージョンをお使いの場合は、Microsoft 365オンラインなどで代用するか、[中古車価格(特徴量作成例)]ワークシートを参照するだけにしてください。
- B列の見出しを右クリックし、[挿入]を選択する(B列の手前に新しい列が挿入される。セルB1に「輸入車」という見出しを入力しておくとよい)
- セルL2に=UNIQUE(A2:A167)と入力する(メーカーの一覧表が作成される)
- セルM2〜M17に、輸入車なら1を、国産車なら0を読者自身が手動で1つずつ入力する
- セルB2に=XLOOKUP(A2:A167,L2:L17,M2:M17,0,0,1)と入力する
- スピル機能が使えない場合は、配列数式として入力する
- Googleスプレッドシートでは=ARRAYFORMULA(XLOOKUP(A2:A167,L2:L17,M2:M17,0,0,1))と入力する
レクサスはトヨタ自動車の高級車ブランドなので、ここでは国産車としておきます。UNIQUE関数を使えば、複数回登場する値を1つにまとめた重複のないリストが作成できます。XLOOKUP関数は、セルA2〜A167のメーカー名をセルN2〜N17から検索し、それに対応するセルO2〜N17の値(0か1の値)を返します。XLOOKUP関数はこの連載の第3回で取り上げましたが、あまりなじみのない方は、こちらで形式を確認しておいてください。
これで新たな特徴量(説明変数)が作成できました。あとはこれまでと同様に重回帰分析を行うだけです。セルアドレスをそのまま使うと見づらいので、あらかじめ以下のような名前を付けてあります(B列の手前に列を挿入すると列番号が変わってしまうので、作成例である[中古車価格(特徴量作成例)]ワークシートの範囲に名前を付けてあります)。
- セルE2〜G167に説明変数1という名前を付けておく(年式、走行、排気量に当たる)
- セルB2〜B167に説明変数2という名前を付けておく(輸入車に当たる)
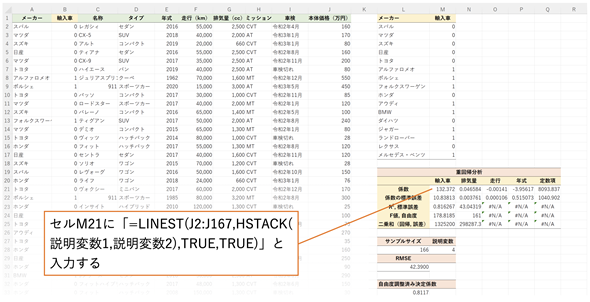
LINEST関数を入力すれば係数や定数項が求められます。ただし、説明変数の範囲が離れた列にあるので、HSTACK関数を使って列をつなぐことにします。セルM21に=LINEST(J2:J167,HSTACK(説明変数1,説明変数2),TRUE,TRUE)と入力してください(図10)。セルJ2〜J167の値は[中古車価格]ワークシートのセルI2〜I167と同じ値なので、本体価格という名前を使って、=LINEST(本体価格,HSTACK(説明変数1,説明変数2),TRUE,TRUE)と入力しても同じ結果になります。
決定係数やRMSEの求め方は既に見た通りです。実際に入力されている式については[中古車価格(特徴量作成例)]をご参照ください。これまで([中古車価格(作成例)]ワークシート)は決定係数が0.6460、RMSEが58.8370でしたが、「輸入車」という特徴量を追加すると、決定係数が0.8163、RMSEが42.3900となり、精度がかなり上がることが分かります。
名義尺度のデータを数値化する
中古車の本体価格に関係があり、数値で表せない値は他にどのようなものがあるでしょうか。
候補として考えられるのは車両のタイプとミッション(変速機の種類)です。スポーツカーやSUVは高価で、コンパクトカーやワゴンは比較的安価であると思われるので、車両のタイプは説明変数の候補として有力です。しかし、車両のタイプは種類が多く、表が大きくなり過ぎてしまうので、ここでは、分かりやすさを優先させることとし、ミッション(CVT、AT、MTの3種類)を例に取り上げます。一概には言えませんが、CVTは比較的小さな車種で、ATは比較的大きな車種で、MTは比較的古い車種やスポーツカーで採用されています。
車検の期限も関係ありそうですが、ここでは名義尺度の変数の取り扱いを見るので、取り上げていません(車検費用は本体価格には含まれないという理由もありますが)。ただし、車検切れかそうでないかといった分け方もアリかと思われます。車検切れの車両はメンテナンスされずに放置されていた、程度のよくないものであると考えられるからです。車検の期限は数値で表せますが、車検の残りがあるということと、車検切れであるということとは質的に異なるというわけです。実際、車検切れの車両は全て100万円未満です。
前項で見たように、カテゴリーが2つに分けられる場合は一方を0、もう一方を1とすればうまくいきました。カテゴリーが3つ以上の場合には、それぞれのカテゴリーを項目にし、一致する場合には1を、一致しない場合には0を入れます。このようにして作られた変数のことをダミー変数と呼びます(図11)。
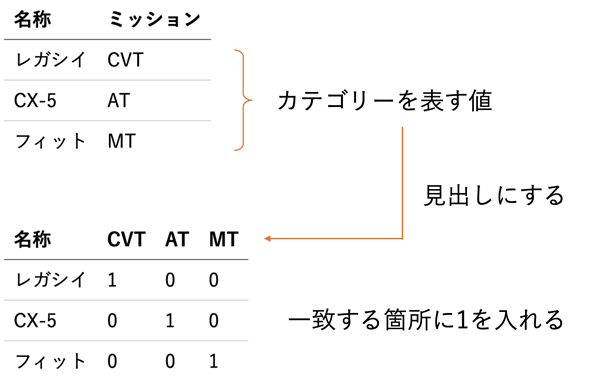
図11 名義尺度のデータをダミー変数で数値化する
カテゴリーを表す名称を項目名とし、一致する場合は1を、一致しない場合は0を入れる。回帰式では、それぞれの変数に係数が掛けられるが、例えば、CVTの中古車はATとMTが0なので、CVTの係数だけが掛けられることになる。
実は、カテゴリーがn個の場合、ダミー変数はn−1個だけで十分です。図11では全てのカテゴリーを項目にしていますが、例えばMTという項目がなくても構いません。CVTとATの両方が0であればMTであることが分かるからです。
では、ダミー変数を用意して重回帰分析を行ってみましょう。やるべきことは単純ですが、手作業だと面倒なのでできるだけ自動化しましょう。[中古車価格(ダミー変数)]ワークシートを開いて、どのような数式が入力されているか確認していただくだけで構いません(図12)。
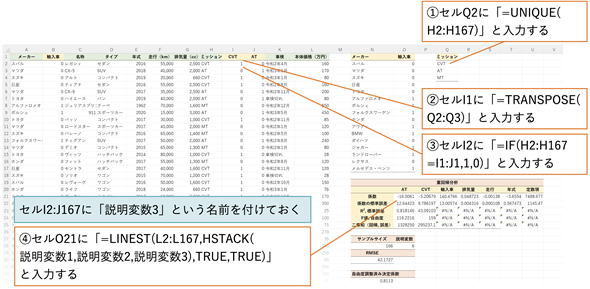
図12 ミッションの違いをダミー変数として表して重回帰分析を行う
UNIQUE関数を使ってミッションのリストを作成し、TRANSPOSE関数を使って行と列を入れ替えれば、見出し(セルI1〜J1)が作成できる。IF関数を使い、H列の値とセルI1〜J1の見出しが等しければ1、等しくなければ0とすればよい。セルI2〜J167に説明変数3という名前を付けておけば、LINEST関数の引数が簡潔になる。
手順は以下の通りです。TRANSPOSE関数は行と列を入れ替えるための関数です。以下の手順でもExcel 2019以前のバージョンではUNIQUE関数が使用できないので、Microsoft 365オンラインなどで代用するか、[中古車価格(ダミー変数)]ワークシートを参照するだけにしてください。
- セルQ2に「=UNIQUE(H2:H167)」と入力する(ミッションの一覧を作成する)
- セルI1に「=TRANSPOSE(Q2:Q3)」と入力する(セルQ2〜Q3を横に並べる)
- セルI2に「=IF(H2:H167=I1:J1,1,0)」と入力する
- スピル機能が使えない場合は、配列数式として入力する
- Googleスプレッドシートでは「=ARRAYFORMULA(IF(H2:H167=I1:J1,1,0))」と入力する
- セルI2〜J167に説明変数3という名前を付けておく
- セルO21に「=LINEST(L2:L167,HSTACK(説明変数1,説明変数2,説明変数3),TRUE,TRUE)」と入力する
決定係数、RMSEの求め方は既に見た通りです。いずれもごくわずかですが改善されたようです。
コラム 重回帰分析の落とし穴 〜 多重共線性にご注意
説明変数を適切に選択すれば、重回帰分析の精度は良くなります。しかし、説明変数を増やせばいいというものでもありません。似たような説明変数を複数使うと、かえって回帰式の精度が悪くなることがあります。このことを多重共線性と呼びます。
多重共線性を検出するには、説明変数同士に強い相関のある項目がないかを確認します。
また、VIFと呼ばれる値も多重共線性の目安となります。VIFは相関行列の逆行列の対角要素の値となるので、MINVERSE関数を使うと簡単に求められます(図13)。一般に、VIFの値が10以上になると多重共線性が疑われるので、説明変数をどれか1つに減らすことを検討する必要があります。[中古車価格(VIF)]ワークシートに例があるので、参照してみてください。
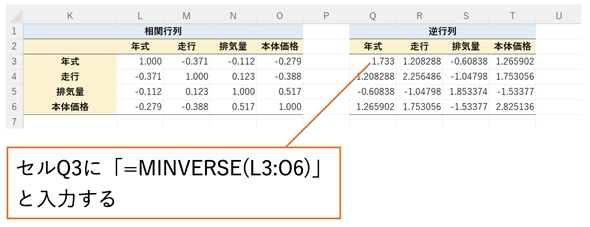
図13 VIFの値を求める
相関行列の逆行列の値をMINVERSE関数で求める。対角要素(セルQ3、R4、S5、T6)の値が10以上になると多重共線性が疑われる。この例では多重共線性は見られない(サンプルファイルには多重共線性が見られる極端な例も含めてある)。
多項式回帰による回帰分析を行う 〜 気温と電気器具によるCO2排出量を例に
ここからは多項式回帰のお話に移ります。この連載の第12回で見たように、気温と電気器具によるCO2排出量はU字形の分布になっていました。ということは下に凸な二次関数で近似できそうです。二次関数は以下のような式で表されますね。
実は、LINEST関数を使うと、このような多項式を利用した回帰分析もできます。単にx2の項を用意するだけです。それ以外の方法はこれまでと全く同じなので、図14でサクッと確認しておきましょう。三次以上の関数でも同様です。
サンプルファイルはこちらからダウンロードできます。[気温とCO2排出量]ワークシートを開いて、入力されている数式を確認してください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
以下の手順については動画も用意してあります。操作方法を一つ一つ丁寧に追いかけたい方はぜひご視聴ください。
動画3 Excelで多項式回帰による回帰分析を行うには
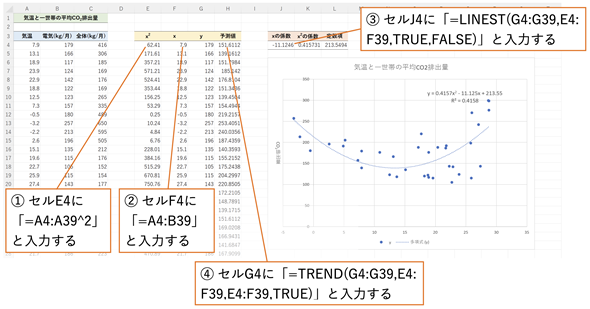
図14 多項式回帰による回帰分析を行う
E列がx2の値、F列とG列はxとyなので、A列とB列の値をそのまま表示してある。目的変数はセルG4〜G39の範囲、説明変数はセルE4〜F39となる。ここでは、LINEST関数の最後の引数にFALSEを指定して、補正項を求めず、係数と定数項だけを求めている。右側の散布図はセルA3〜B39を基に作成したもの。
手順は以下の通りです。散布図は図7のような実測値と予測値の当てはまりの良さを見るためのものではなく、元のデータの散布図とそれに対する近似曲線を描くためのものです。
多項式回帰による回帰分析を行う
- セルE4に「=A4:A39^2」と入力する
- スピル機能が使えない場合は配列数式として入力する
- Googleスプレッドシートでは「=ARRAYFORMULA(A4:A39^2)」と入力する
- セルF4に「=A4:B39」と入力する
- Googleスプレッドシートでは「=ARRAYFORMULA(A4:B39)」と入力する
- セルJ4に「=LINEST(G4:G39,E4:F39,TRUE,FALSE)」と入力する(係数と定数項が求められる)
- セルJ4に「=TREND(G4:G39,E4:F39,E4:F39,TRUE)」と入力する
散布図の作成(Excelでの操作手順)
- セルA3〜B39を選択する
- [挿入]タブを開き、[散布図(X, Y)またはバブルチャートの挿入]ボタンをクリックする
- [散布図]を選択する(これで散布図が作成される)
- 系列(作成された散布図のいずれかの点)を右クリックし、[近似曲線の追加]を選択する
- [近似曲線の書式設定]作業ウィンドウで[多項式近似]オプションをオンにする
- [次数]ボックスに「2」を入力する
- [グラフに数式を表示する]チェックボックスをオンにする
- [グラフにR-2乗値を表示する]チェックボックスをオンにする
散布図の作成(Googleスプレッドシートでの操作手順)
- セルA3〜B39を選択する
- メニューバーから[挿入]−[グラフ]を選択する
- [グラフエディタ]作業ウインドウで[グラフの種類]リストから[散布図]を選択する(これで散布図が作成される)
- [グラフエディタ]作業ウインドウで[カスタマイズ]をクリックする
- [系列]をクリックして下位の設定項目を表示し、[トレンドライン]チェックボックスをオンにする
- [種類]のリストから[多項式]を選択する
- [多項式次数]のリストから「2」を選択する
- [ラベル]のリストから[方程式]を選択する
- [決定係数を表示する]チェックボックスをオンにする
多項式近似の近似曲線の次数は、Excelでは6まで、Googleスプレッドシートでは10まで指定できます。次数を上げると、近似曲線がよりデータの近くを通るようになりますが、あまりにも元のデータへの当てはまりが良くなり過ぎて、未知のデータにうまく当てはまらないことがあります(過剰適合や過学習とも呼ばれます)。過学習が起こっているかどうかを調べるには、元のデータを学習用と検証用にランダムに分け(例えば全体の75%を学習用に、25%を検証用にするなど)、学習用のデータで係数と定数項を求め、検証用のデータでの当てはまりを見るという方法があります(ホールドアウト法と呼ばれます)。
今回は、重回帰分析により回帰式の係数と定数項を求めたり、回帰式を利用して予測を行ったりする方法を紹介しました。また、より良い予測ができるように特徴量を作成したり、名義尺度のデータを数値化したりしました。さらに、多重共線性など、重回帰分析における留意点などについても触れました。最後に、気温と電気器具によるCO2排出量のように、U字形の関係になっている場合にも回帰分析を行うために、多項式回帰を利用する方法も紹介しました。
今回のケーススタディでは、データの形式を整えることの重要性にも気付いたと思います。そこで、次回から数回に分けてデータの形式や取り扱いについて整理したいと思います(本来は分析に先だって知っておくべきことなのですが、実際に分析に取り組んでみないとその必要性を実感しにくいので、あえて後回しにしていました)。というわけで、次回もお楽しみに!
関数リファレンス: この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
相関行列を作成するために使った関数
INDIRECT関数: 参照文字列を基にセルを間接参照する
形式
INDIRECT(参照文字列, 参照形式)
引数
- 参照文字列: セル参照を表す文字列をA1形式またはR1C1形式で指定します。
- 参照形式: 参照文字列の形式を指定する。
- TRUEまたは省略 …… 参照文字列はA1形式で表す。
- FALSE ……参照文字列はR1C1形式で表す。
重回帰分析のために使った関数
LINEST関数: 重回帰分析による回帰式y=a0+a1x1+a2x2+…+anxnの係数a1〜anや定数項a0を求める
形式
LINEST(既知のy, 既知のx, [定数], [補正項])
引数
- 既知のy: 既に得られている目的変数の値(セル範囲)を指定する。
- 既知のx: 既に得られている説明変数の値(セル範囲)を指定する。
- 定数: 定数項a0の値を求めるかどうかを指定する。
- TRUEまたは省略 …… 定数項a0の値を求める
- FALSE …… 定数項a0の値を0とする
- 補正項: 検定などで使われる詳細な情報を求めるどうかを指定する。
- TRUE …… 補正項を求める
- FALSEまたは省略 …… 補正項は求めない(係数と定数項のみを求める)
備考
この関数は係数や定数項などの値を一度に返すので、スピル機能が使えない場合は配列数式として入力する必要がある。係数と定数項の値はan, ... , a2, a1, a0の順に返されることに注意。
TREND関数: 重回帰分析による予測値を求める
形式
TREND(既知のy, 既知のx, 未知のx, [定数])
引数
- 既知のy: 既に得られている目的変数の値(セル範囲)を指定する。
- 既知のx: 既に得られている説明変数の値(セル範囲)を指定する。
- 未知のx: 予測に使いたい説明変数の値(セル範囲)を指定する。このxに対するyの値が求められる。
- 定数: 重回帰式の定数項a0の値を求めるかどうかを指定する。
- TRUEまたは省略 …… 定数項a0の値を求める
- FALSE …… 定数項a0の値を0とする
データの個数を数えるために使った関数
COUNT関数: 数値の個数を求める
形式
COUNT(数値1, 数値2, ... , 数値255)
引数
- 値: 数値の個数を求めたい値やセル範囲を指定する。引数は255個まで指定できる。
COUNTA関数: データの個数を求める
形式
COUNTA(値1, 値2, ... , 値255)
引数
- 値: データの個数を求めたい値やセル範囲を指定する。引数は255個まで指定できる。
備考
COUNT関数は数値の個数を数え、COUNTA関数は数値や文字列、エラー値など全ての種類のデータの個数を数えるのに使う。
データの形式を整える数えるために使った関数
UNIQUE関数: 重複のないデータのリストを作る
形式
UNIQUE(配列, [列の比較], [単一の値])
引数
- 配列: 基となるデータの配列やセル範囲を指定する。
- 列の比較: 検索の方向を指定する。
- TRUE …… 列方向(右に向かって)検索する
- FALSEまたは省略 …… 行方向(下に向かって)検索する
- 単一の値: 1回だけ登場する値を返すかどうかを指定する。
- TRUE …… 1回だけ登場した値のみを返す
- FALSEまたは省略 …… 全ての値について複数回登場した値は1つにまとめて返す
備考
Excelデスクトップ版ではExcel 2021以降のバージョンで使用できる。Microsoft 365オンラインやGoogleスプレッドシートでは使用できる。
TRANSPOSE関数: 行と列を入れ替えた配列を返す
形式
TRANSPOSE(配列)
引数
- 配列: 基となるデータの配列やセル範囲を指定する。
HSTACK関数: 複数の配列を横方向にまとめる
形式
HSTACK(配列1, 配列2, ... , 配列254)
引数
- 配列: 基となるデータの配列やセル範囲を指定する。引数は254個まで指定できる。
備考
HSTACK関数は複数の離れた列を1つの範囲にまとめるのに便利です。複数の配列を縦方向にまとめる(複数の離れた行を1つの範囲にまとめる)にはVSTACK関数が使われます。
逆行列を求めるために使った関数
MINVERSE関数: 逆行列を求める
形式
MINVERSE(配列)
引数
- 配列: 基となるデータの配列やセル範囲を指定する。
備考
引数に指定する配列やセル範囲の行数と列数は同じ(正方行列)である必要があります。
Copyright© Digital Advantage Corp. All Rights Reserved.