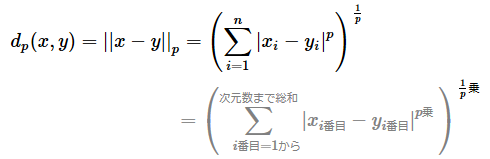ミンコフスキー距離(Minkowski distance)/Lpノルムとは?:AI・機械学習の用語辞典
用語「ミンコフスキー距離」について説明。2点間の距離を計測する方法の一つで、マンハッタン距離(L1ノルム)やユークリッド距離(L2ノルム)、チェビシェフ距離(L∞ノルム)などを一般化したもの。パラメーター「p」の値を調整することで柔軟に距離を表現できる。
用語解説
数学/統計学/機械学習におけるミンコフスキー距離(Minkowski distance)とは、n次元ベクトルで表現される2点(例えばx=[x1,x2,...,xn]とy=[y1,y2,...,yn])間の「距離(ノルム)」を計算するための方法の一つである(具体的な計算方法は後述する)。マンハッタン距離(L1ノルム)や、ユークリッド距離(L2ノルム)、チェビシェフ距離(L∞ノルム)の計算を一般化したものとも見なせる。ミンコフスキー距離は、Lpノルム(Lp norm)とも呼ばれる。
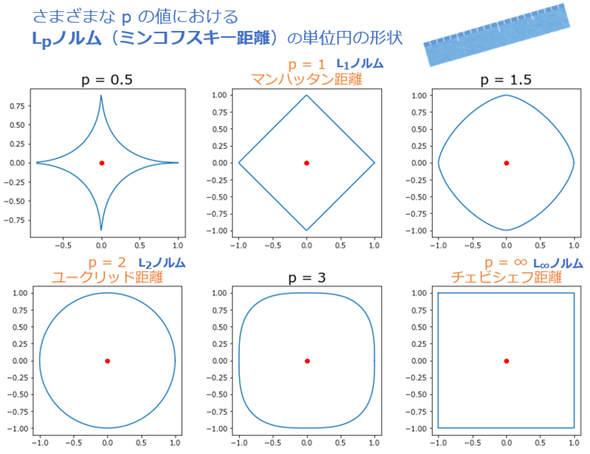
図1は、さまざまなpの値における「Lpノルムの単位円(=全て点の距離が1になる円)」の形状を示している。これは、原点(中心、例えば点x)から1の距離にある点(例えば点y)を連続的に描いて線の図形にしたものだ。例えばp=2の場合、原点から1の距離にある点を満遍なく描いていくと、完全な円形になる(図1の2行1列目)。このように単位円を描くことで、「異なるpの値が、距離の計算方法にどのように影響するか」を視覚的に理解できる。
図1を見ると分かるように、pの値が異なると、単位円の形が変わる。
- 1行1列目: p=0.5の場合、単位円は星形のような形になる(※一般的にはp≧1であるため、この例は特殊であることに注意)
- 1行2列目: p=1の場合、単位円はひし形になる(マンハッタン距離)
- 1行3列目: p=1.5の場合、単位円は丸みを帯びたひし形になる
- 2行1列目: p=2の場合、単位円は完全な円形になる(ユークリッド距離)
- 2行2列目: p=3の場合、単位円は丸みを帯びた正方形になる
- 2行3列目: p=∞の場合、単位円は正方形になる(チェビシェフ距離)
「ミンコフスキー距離(Lpノルム)」の定義と数式
点xから点yのミンコフスキー距離(Lpノルム)を求める数式は、以下のように定義できる。
この数式では、2つのn次元ベクトルで各成分の差の絶対値を取り、それらの絶対値のp乗を合計し、その合計値の1/p乗(p分の1乗)を「距離」として採用している。pには基本的に1以上の実数を指定する。
||……||という数学記号は、ベクトル空間における「長さ/距離」を表現する概念であるノルム(norm)を意味する。Lpノルムは、pの値によって異なる種類の距離を表現する。前述した通り、p=1の場合はマンハッタン距離、p=2の場合はユークリッド距離、p=∞の場合はチェビシェフ距離となる。
ちなみにLpノルムは、NumPyライブラリのnp.linalg.norm(<x-y点間距離の多次元配列データ>, ord=<pの値>)関数で計算できる。
pの値の調整について
パラメーターpの値を調整することで、データ間の距離を柔軟に表現できる。例えば顧客をグループ分け(=機械学習のクラスタリング)する場合、データ間の類似性をミンコフスキー距離で評価する際には、データの特徴やクラスタリングの目的に合わせてpの値を調整することで、クラスタリングの精度を向上させることができる。
ミンコフスキー距離は、p=1(マンハッタン距離)の場合には差が小さい成分も考慮するのに対し、p=∞(チェビシェフ距離)の場合には差が大きい成分のみを考慮するようになる。p=2(ユークリッド距離)の場合は、それらの中間ぐらいで各成分を考慮する。
Copyright© Digital Advantage Corp. All Rights Reserved.