ダイス係数(Dice coefficient)とは?:AI・機械学習の用語辞典
用語「ダイス係数」について説明。集合間の類似性を評価する尺度で、「2つの集合の共通部分が、それぞれの集合の大きさと比べて、どれだけ大きいか」を測定するために使用される。値が1に近いほど「似ている」を、0に近いほど「似ていない」を意味する。少数の一致でもその正確性が重要視される場面で利用されている。
用語解説
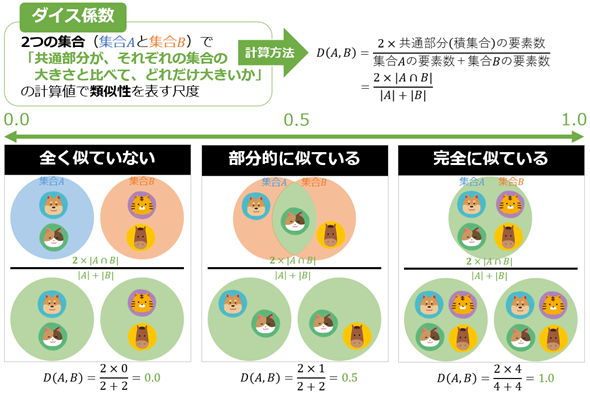
数学/統計学/機械学習におけるダイス係数(Dice coefficient)とは、2つの集合で「それらの共通部分が、それぞれの集合の大きさと比べて、どれだけ大きいか」の計算値で類似性を表す尺度である。具体的には、「2つの集合の共通部分(=積集合:∩)」に含まれる要素数を2倍し、それを「2つの集合それぞれの要素数の合計(=2つの集合に含まれる要素数の平均を2倍した値に相当)」で割ることで計算される(図1)。
このダイス係数の値は、0〜1の範囲に正規化され、1は「完全に一致している(=似ている)」、0は「全く共通点がない(=似ていない)」ことを意味する。ダイス係数は、共通部分を強調するため、重複する要素が少しでもあると、それが強調されて類似度が高くなる傾向がある。
ダイス係数は、ソーレンセン・ダイス係数(Sørensen-Dice coefficient)とも呼ばれることがある。
定義と数式
すでに図1と冒頭の解説で計算方法に言及しているが、あらためて数式としてまとめ、計算例を示しておく。
この2つの集合のダイス係数、すなわち「2つの集合の共通部分(=2つの集合に共通の要素数の2倍)が、それぞれの集合の大きさ(=2つの集合に含まれる要素数の合計)と比べて、どれだけ大きいか(=割合)」を求める数式は、以下のように表される。なお、∩という数学記号は「集合の共通部分」(=積集合:「かつ」と同じ意味)を表し、|……|は集合の要素数を表す。
つまり、|A ∩ B|は「集合Aと集合Bの共通部分」に含まれる要素数を表し、|A|と|B|はそれぞれの集合の要素数を表す。
このダイス係数の数式は、「2つの集合に共通の要素数を、2つの集合に含まれる要素数の平均値で割る」計算と同じ意味を持つ。この数式によって計算されるダイス係数の値は、先ほども説明した通りに0〜1の範囲に収まる。
例えば、集合Aが{1, 2}という2個の要素を含み、集合Bが{2, 3}という2個の要素を含む場合、A ∩ Bは{2}で1個の要素となり、|A|+|B|は2+2=4個の要素である。この場合のダイス係数は、以下のように計算され、0.5となる。
この結果は、「集合Aと集合Bが半分程度、似ている」ことを意味する。つまり、2つの集合は「似ている」とも「似ていない」とも言えない中間的な状態にある。
前述した通り、ダイス係数は、値が1に近いほど類似しており、0に近いほど類似していないことを示す。中間的な値については、状況によってその解釈が異なるため、目的に応じて柔軟に判断することが重要である。
前掲の図1の例も同様に説明すると、以下のようになる。
- 集合Aが{犬, 猫}の2要素、集合Bが{虎, 馬}の2要素である場合、A∩Bは{ }の0要素であり、|A|+|B|=2+2=4要素となるので、ダイス係数は(2×0)÷4=0.0である。
- 集合Aが{犬, 猫}の2要素、集合Bが{猫, 馬}の2要素である場合、A∩Bは{猫}の1要素であり、|A|+|B|=2+2=4要素となるので、ダイス係数は(2×1)÷4=0.5である。
- 集合Aが{犬, 虎, 猫, 馬}の4要素、集合Bが{犬, 虎, 猫, 馬}の4要素である場合、A∩Bは{犬, 虎, 猫, 馬}の4要素であり、|A|+|B|=4+4=8要素となるので、ダイス係数は(2×4)÷8=1.0である。
用途
ダイス係数は、ジャッカード類似度と非常に似た指標であるが、数式における分数の分子にある共通部分(A ∩ B)をより強調して評価する特徴がある。例えば、図1の「部分的に似ている」の例では、ダイス係数が0.5と計算されているが、同じ内容でジャッカード係数を計算すると0.333...となる。このように、共通部分がより高く評価される。
この性質があるため、2つの集合に少しでも一致がある場合に、その一致を高く評価したいケースに有効である。特に、予測の一致が重要な二値分類タスクでは、少数の一致でもその正確性が重要視されるため、ダイス係数がよく利用される。例えば、病変部位の検出など、正確な発見が求められる医療画像解析(主にセグメンテーションタスク)でも、ダイス係数は広く利用されている。
さらに、データを集合として扱うさまざまな分野でダイス係数は利用されている。例えば、クラスタリング(例:図1のような「動物のグループ分け」)では、クラスタ間で少数の一致を重視したい場合に有効である。また、自然言語処理においても、文書やテキストの類似度を評価するために使用されることがある。
ちなみに、二値分類タスクの評価指標であるF1スコア(F1-score)の計算式は、ダイス係数の計算式と同じ意味を持つため、「ダイス係数(Dice coefficient)」と呼ばれることもある。F1スコアも、共通部分(=混同行列の「TP:True Positive」、つまり陽性として正しく分類された部分)を強調して評価する指標である。F1スコアは分類タスクの性能評価において、ダイス係数は集合の類似性評価において、それぞれ活用されている。
API
ダイス係数は、(筆者が調べた限りでは)多くのライブラリで計算式を手動で記述する必要がある。
なお、SciPyライブラリにはdice関数があるが、これは本稿で説明した一般的な「ダイス係数」ではなく、ダイス「非」類似度(Dice “dis”similarity)を計算するものであるため、注意が必要だ。ただし、1−ダイス非類似度(1からダイス非類似度を引く)という計算をすることで、一般的な「ダイス係数」を求めることができる。
また、PyTorchの基本ライブラリには含まれないが、PyTorch LightningライブラリにはDiceクラスがあり、PyTorch IgniteライブラリにはDiceCoefficientクラスが含まれている。これらのクラスは、(各APIドキュメントの説明を筆者が読んだ限りでは)厳密には分類タスクの評価時に混同行列を使ってF1スコア(別名:ダイス係数)を計算するためのものであるため、注意が必要だ。PyTorch LightningのDiceクラスは、(筆者が試した限りでは)一般的な「ダイス係数」の計算にも応用できる。
Copyright© Digital Advantage Corp. All Rights Reserved.