オーバーラップ係数(Overlap coefficient)/シンプソン係数(Szymkiewicz-Simpson coefficient)とは?:AI・機械学習の用語辞典
用語「オーバーラップ係数」について説明。集合間の類似性を評価する尺度で、「2つの集合の共通部分が、いずれかの集合のうち小さい方の集合の大きさと比べて、どれだけ大きいか」を測定するために使用される。値が1に近いほど「似ている」を、0に近いほど「似ていない」を意味する。部分的な一致が重要視される場面で利用されている。
用語解説
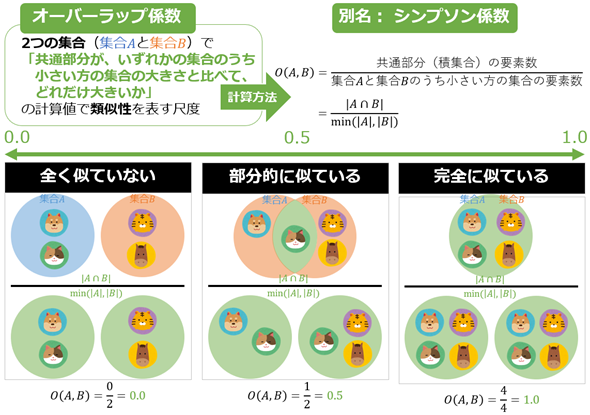
数学/統計学/機械学習におけるオーバーラップ係数(Overlap coefficient)とは、2つの集合で「それらの共通部分が、いずれかの集合のうち小さい方の集合の大きさと比べて、どれだけ大きいか」の計算値で類似性を表す尺度である。具体的には、「2つの集合の共通部分(=積集合:∩)」に含まれる要素数を、「2つの集合のうち、より小さい方の集合」の要素数で割ることで計算される(図1)。
このオーバーラップ係数の値は、0〜1の範囲に正規化され、1は「完全に一致している(=似ている)」、0は「全く共通点がない(=似ていない)」ことを意味する。オーバーラップ係数は、小さい方の集合を基準に類似度を評価するため、同じく類似度の尺度であるジャッカード係数やダイス係数では見逃される可能性のある「部分的な一致」を強調したい場合に有効である。例えば、大規模な文書データの中から「特定のトピックに関連する文書」(=部分的な一致)を見つけ出す際などで有用である。
オーバーラップ係数は、シンプソン係数(Simpson coefficient、正確には「Szymkiewicz-Simpson coefficient:シムキエヴィチ・シンプソン係数」)とも呼ばれることがある。日本語圏では「シンプソン係数」という呼び名の方が通りがよいが、英語圏では「Overlap coefficient」という呼び名が一般的である。なお、生物学には「Simpson's Diversity Index(シンプソンの多様性指数)」という用語があるので、これと混同しないように注意してほしい(恐らくこういう誤解を防ぐため、英語圏では「Overlap coefficient」という呼び名の方が一般的なのではないだろうか)。
定義と数式
すでに図1と冒頭の解説で計算方法に言及しているが、あらためて数式としてまとめ、計算例を示しておく。
この2つの集合のオーバーラップ係数、すなわち「2つの集合の共通部分(=共通の要素数)が、それぞれの集合のうち小さい方の集合の大きさ(=小さい方の集合の要素数)と比べて、どれだけ大きいか(=割合)」を求める数式は、以下のように表される。なお、∩という数学記号は「集合の共通部分」(=積集合:「かつ」と同じ意味)を表し、|……|は集合の要素数を表す。
つまり、|A ∩ B|は「集合Aと集合Bの共通部分」に含まれる要素数を表し、min(|A|, |B|)は2つの集合のうち小さい方の集合の要素数を表す。この数式によって計算されるオーバーラップ係数の値は、先ほども説明した通りに0〜1の範囲に収まる。
例えば、集合Aが{1, 2}という2個の要素を含み、集合Bが{2, 3, 4}という3個の要素を含む場合、A ∩ Bは{2}で1個の要素となり、min(|A|, |B|)は少ない方の2個の要素である。この場合のオーバーラップ係数は、以下のように計算され、0.5となる。
この結果は、「集合Aと集合Bが半分程度、似ている」ことを意味する。つまり、2つの集合は「似ている」とも「似ていない」とも言えない中間的な状態にある。
前述した通り、オーバーラップ係数は、値が1に近いほど類似しており、0に近いほど類似していないことを示す。中間的な値については、状況によってその解釈が異なるため、目的に応じて柔軟に判断することが重要である。
前掲の図1の例も同様に説明すると、以下のようになる。
- 集合Aが{犬, 猫}の2要素、集合Bが{虎, 馬}の2要素である場合、A∩Bは空集合({ })の0要素であり、min(|A|, |B|)=2要素となるので、オーバーラップ係数は0÷2=0.0である。
- 集合Aが{犬, 猫}の2要素、集合Bが{猫, 虎, 馬}の3要素である場合、A∩Bは{猫}の1要素であり、min(|A|, |B|)=2要素となるので、オーバーラップ係数は1÷2=0.5である。
- 集合Aが{犬, 虎, 猫, 馬}の4要素、集合Bが{犬, 虎, 猫, 馬}の4要素である場合、A∩Bは{犬, 虎, 猫, 馬}の4要素であり、min(|A|, |B|)=4要素となるので、オーバーラップ係数は4÷4=1.0である。
用途
オーバーラップ係数には、冒頭でも説明したように「小さい方の集合に基づいて類似性を評価する性質」があるため、(主に、異なるサイズの集合を比較する場合において)部分的な一致を強調したいケースに有効である。特に、大規模なデータセットの中から特定のパターンや要素を見つけ出す際、部分的な一致が重要となる分析に適している。例えば、大量のテキストデータの中から関連性のある文書を抽出する自然言語処理タスクでも、オーバーラップ係数が活用されることがある。
また、オーバーラップ係数は、データを集合として扱う多様な分野で利用されている。例えば、クラスタリング(例:図1のような「動物のグループ分け」)において、異なるクラスタ間での部分的な一致を重視したい場合に有効である。また、画像認識やパターン認識においても、オーバーラップ係数を使って、部分的な一致が重要な分析や分類タスクに役立てられることがある。
さらに、機械学習とは関係ないが、集合の部分的な一致を強調する性質から、バイオインフォマティクスや遺伝学など、特定の遺伝子や配列の一致を評価する際にも利用されることがある。
3つの「集合の類似度」指標の使い分け指針
オーバーラップ係数(=シンプソン係数)は、ジャッカード係数(=ジャッカード類似度)やダイス係数と非常に似た指標であるため、これらの使い分け指針を示しておこう。
3つの計算例を比較すると、図1の「部分的に似ている」の例と同じ内容で計算すると、
- ジャッカード係数: 1÷4=0.25(計算式:共通部分の要素数÷集合全体の要素数)
- ダイス係数: (2×1)÷(2+3)=0.4(計算式:2×共通部分の要素数÷両集合の要素数の合計)
- オーバーラップ係数: 1÷2=0.5(計算式:共通部分の要素数÷小さい方の集合の要素数)
となる。この例が示す通り、同じデータに対してそれぞれの類似度を計算した場合、通常は、
ジャッカード係数 ≦ ダイス係数 ≦ オーバーラップ係数
という大小関係になる。この関係性を踏まえて、使い分けの指針を以下にまとめる(※ただし、併用するケースもあり得る)。
- ジャッカード係数(Jaccard coefficient): (部分的な一致や少数の一致を重視せず)全体的な一致で類似度を厳密に評価したい場面で有用。主に一般的なクラスタリングや文書検索など。
- ダイス係数(Dice coefficient): 少数の一致でも正確性が重要視される場面(=共通する要素が少なくても、その一致を両集合の平均的な大きさを基準に強調する場面)で有用。例えば、正確な発見が求められる医療画像のセグメンテーションタスクなど。
- オーバーラップ係数(Overlap coefficient): 部分的な一致が重要視される場面(=全体として異なる要素が多い中で、共通部分を小さい方の集合を基準に評価したい場面)で有用。例えば、多数の文書から特定のトピックやキーワードに関連する文書を探し出すタスクなど。
ダイス係数とオーバーラップ係数の違いは分かりづらいかもしれないので、繰り返しになるが、少し説明を補足しておこう。
ダイス係数の「少数の一致」では、「共通する要素の数」に注目するのがポイントだ。例えば{犬, 猫}と{猫, 虎, 馬}という集合がある場合、共通する要素が少なくても、{猫}1つが一致していることに注目する。その少数の一致が類似性の評価において大きな意味を持つ場面に、ダイス係数は適している。
一方で、オーバーラップ係数の「部分的な一致」では、「共通部分が小さい集合を基準にどれだけ占めているか」に注目するのがポイントだ。例えば{犬, 猫}と{猫, 虎, 馬}という集合がある場合、全体として異なる要素が多い中で、{猫}という共通部分が「小さい方の集合に対して、どれだけ大きな割合を占めているか」に注目する。共通部分が持つ影響力の大きさ(=占める割合)を類似性の評価に反映させたい場面に、オーバーラップ係数は適している。
Copyright© Digital Advantage Corp. All Rights Reserved.