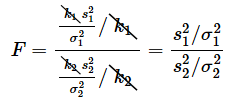検索
連載

［データ分析］F分布 〜 2つの農法で果物の糖度が安定しているのはどちら？：やさしい確率分布

データ分析の初歩から学んでいく連載（確率分布編）の第9回。F分布は分散の比に関連する分布です。2つの母集団から取り出されたサンプルを基に「それぞれの母集団の分散に違いがあるのか」を調べる場合などに使われます。F分布の確率変数と自由度の求め方を見た後、その確率密度関数や累積分布関数について解説します。

Share
Tweet
LINE
Hatena
「やさしい確率分布」のインデックス

連載目次

連載：

『社会人1年生から学ぶ、やさしい確率分布』

社会人1年生から学ぶ、やさしいデータ分析

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載（記述統計と回帰分析編）の続編で、確率分布に焦点を当てています。
　この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムや統計ソフト「R」などでの作成例にも触れることにします。
　数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博
羽山博

筆者紹介： IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば（すり抜けキケン、制限速度守ってね！）。


　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第9回です。前回は、平均値に関連する分布として、t分布を取り上げました。今回は分散の比に関連するF分布について、その特徴や意味を基本から解き明かし、確率密度関数／累積分布関数の求め方、利用例などを見ていきます。

果物の糖度が安定する農法はどちら？ 〜 F分布の利用

　「糖度の高い果物」と言えば、皆さんは何を思い浮かべるでしょうか。筆者は巨峰などのぶどうを思い浮かべます。一般に、巨峰の糖度は18〜20といわれており、果物の中ではかなり高い方です。果物を育てるに当たっては、糖度などの品質が高いこと、形が良いこと、収量が大きいことなど、考慮すべき事柄が数多くありますが、品質が安定していることも重要かと思います。

　図1は、異なる2つの農法で育てたぶどうの木からサンプルを幾つか取り出して糖度を求めたイメージです（ただし、架空の例です）。サンプルの値を見ると、農法Bの方が糖度の分散が小さい（＝品質が安定している）ように思われます。このように、農法Aと農法Bでは分散が異なるのか（農法Bが分散が小さいのか）といったことが、今回の問題意識です。要するに、分散を比較したいというわけです。

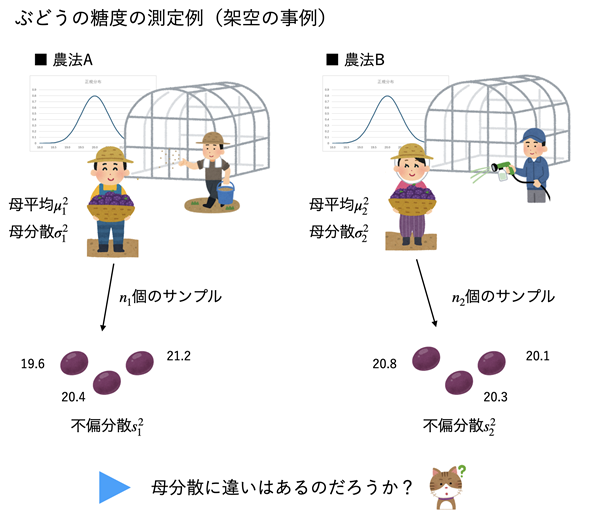
今回の問題意識
図1　2つの農法で育てたブドウの糖度に母分散の違いはあるのか？
図中には記していないが、農法Aの不偏分散はs12＝0.64、農法Bの不偏分散はs22＝0.13となっている。この結果から、「農法Aよりも農法Bの母分散が小さい＝品質が安定している」と言えそうだが、果たしてどうなのか。それを知るためにはF分布の知識が必要となる。

　分散を比較するには、分散の比を求めます。差（引き算）じゃなくて比（割り算）なんですか、と思われる方も多いと思います。それは、分散が二乗された値だからです。ちょっとした例え話をしてみましょう。

　二乗した値で最も身近なものは面積ですね。公園などの広さをイメージするのに、よく「東京ドーム何個分」と表現することがあります。例えば、東京都立川市にある昭和記念公園の面積は約1.8km2（公開されている場所は約1.69km2）で、東京ドームの面積は約0.047km2です。従って、昭和記念公園の面積は、東京ドームの1.8/0.047＝38.298個分ということになります。これは、比（割り算）を使った計算ですね。面積を比較するのに、差を取って1.8−0.047＝1.753km2だ、などという比較はしません。それと同じ考え方です。

　分散の比に関する分布はF分布と呼ばれます。そこで、F分布の確率変数はどのようなものか、というところから出発し、その後、F分布の確率密度関数と累積分布関数を可視化していきましょう。

分散の比に関する分布 〜 F分布の確率変数

　理屈は後回しにして、F分布の確率変数がどのように定義されるかを示しておきます。異なる2つの正規母集団から独立にサンプルを取り出すことを考えてみましょう。例えば、農法Aで育てられたぶどうの糖度が母平均μ1、母分散σ12の正規分布に従い、農法Bで育てられたぶどうの糖度が母平均μ2、母分散σ22の正規分布に従うといった場合です。

　このとき、それぞれの母集団からサンプルを取り出してカイ二乗値χ12,χ22を求めると、確率変数Fは、

と定義されます。k1,k2はそれぞれの自由度です。この確率変数が自由度（k1,k2）のF分布F(k1,k2)に従います。取り出したサンプルサイズがn1個、n2個の場合、k1＝n1−1,k2＝n2−1ですね。

　（1）式を見ると、F値はカイ二乗値を自由度で割った値の比になっていることが分かります。カイ二乗分布はこの連載の第7回で見た通り、分散に関する分布です。このことから、F分布は分散の比に関する分布であることが分かります。

　さらに、それぞれのサンプルから求めた不偏分散がs1、s2であるとすると、（1）式は以下のように変形できます。

　（1）式を（2）式に変形する手順については、後のコラムで解説します。s12/σ12やs22/σ22は、不偏分散と母分散との比ですね。つまり、サンプルから推定された母分散と、母分散との違いを表します。（2）式はそれらの比となっています。

　しかし、これだけではイメージが湧かないと思われるので、（2）式に具体的な数値を幾つか当てはめて意味を考えてみましょう。母集団Aと母集団Bの母分散をそれぞれσ12＝0.3, σ22＝0.2と仮定すると、

  • ケース1： s12＝0.3, s22＝0.4の場合（母集団Aに比べて、母集団Bのサンプルから求めた不偏分散が母分散に対して大きい場合）は、
  • ケース2： s12＝0.3, s22＝0.2の場合（いずれも、母分散と不偏分散が等しい場合）は、
  • ケース3： s12＝0.6, s22＝0.2の場合（母集団Aに比べて、母集団Bのサンプルから求めた不偏分散が母分散に対して小さい場合）は、

となります。

　母集団から数多くのサンプルを取り出した場合は、不偏分散は母分散に近くなります。その場合、当然のことながらケース2に近くなるはずです。

　というわけで、F分布の確率密度関数は自由度が大きくなるとF＝1.0の辺りに山があることが想像されます（これについては後述します）。母集団Aに比べて、母集団Bの不偏分散が大きい場合はF値が小さくなり、母集団Bの不偏分散が小さい場合はF値が大きくなることも分かります。

　では、次にF分布の確率密度関数の値を求めて、可視化してみましょう。

F分布ってどんな感じの分布（1） 〜 確率密度関数を可視化してみよう

　F分布の確率密度関数f(x;k1,k2)と累積分布関数F(x;k1,k2)は以下の式で表されます（確率変数xと自由度k1,k2を;で区切って表記しています）。例によって、これらの式を覚える必要は全くありません。ExcelのF.DIST関数を使えば簡単に答えが求められるので、軽くスルーしてください。

　ただし、k1,k2は自由度、Izは正則化された不完全ベータ関数で、

です。なんだか、目が回りそうな数式ですね。後のコラムでこの定義通りに計算した例も紹介しますが、ExcelのF.DIST関数を使ってF分布の確率密度関数と累積分布関数を可視化してみましょう。

　F.DIST関数を使って、x＝0.0〜6.0に対する確率密度関数の値を求め、グラフを描いてみます。F分布の母数は自由度のみです。つまり、自由度が決まれば、F分布の形も決まります。

　先に、F.DIST関数の形式を見ておきましょう。

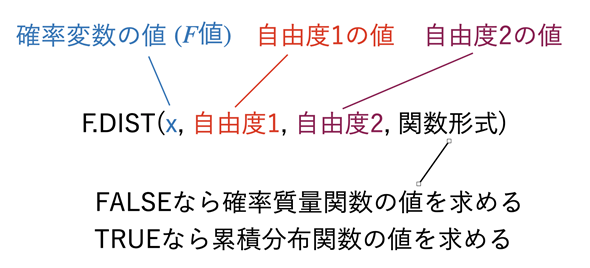
F.DIST関数の形式
図2　F.DIST関数に指定する引数
F.DIST関数には、確率変数の値（F値）と「自由度1」「自由度2」を指定する（※「自由度が1」「自由度が2」という意味ではなく、「1番目の自由度」「2番目の自由度」という意味です）。関数形式についてはこれまで見てきた関数と同様、FALSEを指定すれば確率密度関数の値が、TRUEを指定すれば累積分布関数の値が求められる。

　図3が、幾つかの自由度に対するF分布の確率密度関数の値を求めてグラフを描いた例です（累積分布関数については次の項で取り扱います）。作成の手順は図の後に記しておきます。

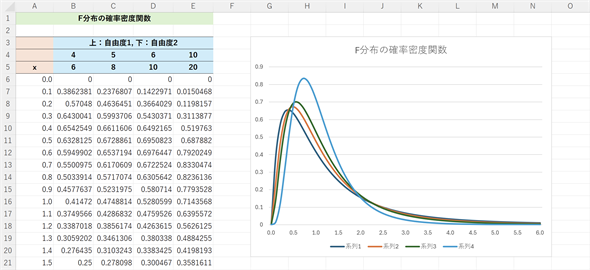
F分布の確率密度関数
図3　F分布の確率密度関数の例
自由度1は4, 5, 6, 10とし、それらに対応する自由度2を6, 8, 10, 20として、x＝0.0〜6.0までの確率密度関数の値を求め、グラフを描いてみた。xと表記されているA列の値が確率変数（F値）であることに注意。B〜E列はそれぞれの自由度に対する確率密度関数の値。グラフ作成の手順は後の箇条書きを参照。

　確率密度関数の値を求めるための手順は以下の通りです。可視化については単に折れ線グラフを描くだけなので、関数の入力にのみ焦点を当てることにします。グラフ作成の手順についてはサンプルファイル内に掲載しておきます。

　サンプルファイルをこちらからダウンロードし、［F分布］ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから［ファイル］−［コピーを作成］を選択し、Googleドライブにコピーしてお使いください。

◆ Excelでの操作方法

  • セルB6に=F.DIST(A6:A66,B4:E4,B5:E5,FALSE)と入力する
    • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB6〜E66）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す

◆ Googleスプレッドシートでの操作方法

  • セルB6に=ARRAYFORMULA(F.DIST(A6:A66,B4:E4,B5:E5,FALSE))と入力する

● グラフの作成方法

  • サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

　F分布の台（確率変数が取り得る値の範囲）は0〜∞です。図3では、そのうちの0.0〜6.0の範囲をグラフ化しています。グラフを見て、まず気付くのはF分布の確率密度関数が左右対称でないことでしょう。また、自由度が大きくなると、山の最も高くなる位置がx＝1.0の（つまりF値が1.0である）位置に近づいていくことも分かります。


AI博士

　F分布の期待値（平均）はk2/(k2−2)です。従って、正確には自由度2が大きくなると山の最も高くなる位置がx＝1.0に近づくということになります。ただし、グラフが左右対称ではなく、山が左に寄っていて、右側に裾が広がる形になっているので、実際には山の最も高くなる位置は少し左にずれます。

　ちなみに自由度1が大きくなると山の中心付近が高くなり、裾がより広がります。図3でもある程度分かりますが、サンプルファイルで自由度1や自由度2を大きく変えてみるとそのことが分かるので、いろいろと試してみて下さい。


F分布ってどんな感じの分布（2） 〜 累積分布関数を可視化してみよう

　続いて、累積分布関数です。こちらは、自由度(10, 20)、x＝0.0〜4.0の例だけを見ておきます（図4）。確率密度関数でグラフとx軸で囲まれた範囲の面積が累積分布関数の値になることを示すために、確率密度関数も併せて作成し、説明をグラフ上に書き加えてあります。［F分布累積］ワークシートを開いて、図の後の手順で試してみてください。グラフ作成の手順についてはサンプルファイル内に掲載しておくこととします。

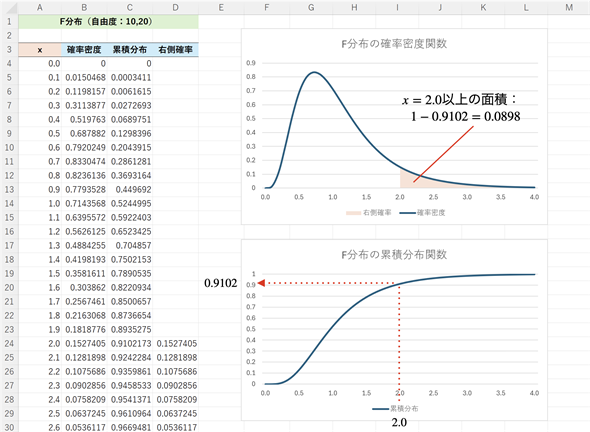
F分布の累積分布関数
図4　F分布の累積分布関数の例
上のグラフが確率密度関数のグラフ。グラフとx軸で囲まれた範囲の面積（この例では塗りつぶした部分以外の面積）が累積分布関数の値になる。塗りつぶした部分は右側確率に当たる。下のグラフは累積分布関数の値をプロットしたもの。例えば、x＝2.0に対する累積分布関数の値は0.9102となる。右側確率は1−0.9102＝0.0898。

　確率密度関数の値を求める方法は既に見た通りですが、x＝2.0〜4.0の範囲を塗りつぶして表示するために使うので、併せて記しておきます。

◆ Excelでの操作方法

  • 確率密度関数の値を求める
    • セルB4に=F.DIST(A4:A44,10,20,FALSE)と入力する
      • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルB4〜B44）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
  • 累積分布関数の値を求める
    • セルC4に=F.DIST(A4:A44,10,20,TRUE)と入力する
      • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルC4〜C44）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
  • 右側確率を塗りつぶすための確率密度関数の値を求める
    • セルD4に=IF(A4:A44<2,#N/A,B4:B44)と入力する
      • 古いバージョンのExcelでスピル機能が使えない場合は、結果が求められるセル範囲（セルD4〜D44）をあらかじめ選択しておき、関数を入力した後、入力の終了時に［Ctrl］＋［Shift］＋［Enter］キーを押す
    • セルD4〜D44にはあらかじめ条件付き書式を設定し、値が#N/Aのセルの文字色を白にして見えなくしてあります（操作はサンプルファイルを参照）

◆ Googleスプレッドシートでの操作方法

  • 確率密度関数の値を求める
    • セルB4に=ARRAYFORMULA(F.DIST(A4:A44,10,20,FALSE))と入力する
  • 累積分布関数の値を求める
    • セルC4に=ARRAYFORMULA(F.DIST(A4:A44,10,20,TRUE))と入力する
  • 右側確率を塗りつぶすための確率密度関数の値を求める
    • セルD4に=ARRAYFORMULA(IF(A4:A44<2,#N/A,B4:B44))と入力する
    • セルD4〜D44にはあらかじめ条件付き書式を設定し、値が#N/Aのセルの文字色を白にして見えなくしてあります（操作はサンプルファイルを参照）

● グラフの作成方法

  • サンプルファイル内に掲載しておきます（タイトルや軸の書式などの細かい設定は省略）

農法の違いにより糖度のばらつきは異なるのか？

　さて、冒頭のお話の続きです。農法Aと農法Bとで母分散に違いがあるかどうか（農法Bの母分散の方が小さいのか）を知りたいということでした。まず（2）式を再掲します。

　この式を基にF値を求めたいのですが、そもそも母分散が分かっていません。そこで、母分散が等しいと仮定しましょう。それが否定できれば母分散に違いがあることになりますね。つまり、（2）式でσ12＝σ22であるものとします。すると、

となります。不偏分散の比がそのままF値になるというわけです。

　s12よりもs22の値が大きければF値が小さくなり、累積確率も小さくなります。逆に、s12よりもs22の値が小さければF値が大きくなり、右側確率が小さくなります。前者は確率密度関数のグラフで、横軸の値が小さくなった場合に当たり、後者は大きくなった場合に当たります（図5）。

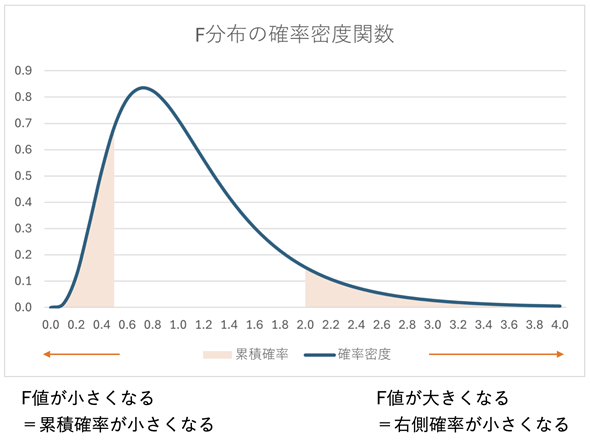
F値と累積確率
図5　F値の大小と累積確率、右側確率
不偏分散の比（F値）が小さくなると、累積確率が小さくなる。逆に不偏分散の比が大きくなると、右側確率が小さくなる。不偏分散の比が1に近いと累積確率はグラフの半分の面積の0.5に近くなる。

　では、以下の表1に示すサンプルで確認してみましょう。母分散が等しいと仮定すると、不偏分散の比、つまりF値が極端に小さくなる（累積確率が小さくなる）ことはないはずです。逆に、F値が極端に大きくなる（右側確率が小さくなる）こともないはずです。……が、そういった確率の小さなことが起こったのであれば、母分散が等しいという仮定を棄（す）てなければなりませんね。

農法 サンプル
A 19.3　20.6　20.7　19.7　19.4　20.2　20.3　20.2　20.7　19.5
B 20.1　19.9　19.7　20.4　20.2　20.7　20.4　19.9　20.9　20.4
表1　農法Aと農法Bから取り出したサンプルの値（糖度）

　図6は、これらの値を基にそれぞれの不偏分散を求め、F値とそれに対する累積確率と右側確率を求めたものです。［応用例］ワークシートを開き、図中に示した手順で試してみてください。

F値と累積確率
図6　F値の大小と累積確率、右側確率
農法Aと農法Bのサンプルの値は縦方向に入力されている。不偏分散を求めると農法Bのばらつきが小さいように見える。セルF4で求めた不偏分散の比がF値となる。F値を基にセルF6で右側確率を求めると0.141（＝14.1％）となる。自由度は9であることに注意。

　結果は14.1％となります。一般に、5％あるいは1％以下であれば「まれにしか起こらないこと」と考えられ、母分散が等しいと仮定するには無理がある（農法Bの母分散が小さい）ということになります。しかし、この場合、比較的小さな値であるとはいえ、母分散が等しいという仮定を捨てるほどではないようです。つまり、農法Bの母分散が小さいとは言えないということになります（といっても、仮説を棄（す）てられないというだけなので、等しいと断定することはできません）。

　実は、この計算は等分散の検定のための計算にほかなりません。ただし、帰無仮説や対立仮説などの考え方を十分に知った上で使う必要があるので、この時点で「結論はこうだ！」と言い切るのは少し待ってください。等分散の検定については推測統計編でお話しします。

F分布の累積分布関数に対する逆関数は？

　F.INV関数やF.INV.RT関数を使えば、F分布の累積分布関数に対する逆関数の値が求められます。

　F.INV関数には左側確率と自由度1、自由度2を指定し、T.INV.2T関数には右側確率と自由度1、自由度2を指定します。例えば、自由度1が6、自由度2が10のF分布で、累積確率（左側確率）が95％のときのF値は=F.INV(95%, 6, 10)で求められます。結果は3.217となります。この確率は、右側確率が5％のときのF値と等しくなるので、=F.INV.RT(5%, 6, 10)の結果と一致します。空いているセルにこれらの式を入力してみて確認しておいてください。

　なお、これらの例は［F分布の逆関数］ワークシートに入力されています。F分布の累積分布関数に対する逆関数の値は、母分散の比の区間推定などに使われます。詳細は推測統計編でお話しします。

　ここまで、F分布の確率変数と確率密度関数、累積分布関数について見てきました。また、応用例として、等分散の検定につながるお話にも（かなり）踏み込みました。ここからは、数式やシミュレーションによってF分布についての理解を深めていきたいと思います。実用的には知らなくてもあまり問題がないので、数式が苦手な方は、最後の「この記事で取り上げた関数の形式」を確認して、今回はお開きとしてもらっても構いません。

コラム　F分布とカイ二乗分布、不偏分散の関係

　冒頭で見た（1）式を（2）式に変形する手順を解説します。（1）式と（2）式をそれぞれ再掲しておきましょう。

　母平均が未知の場合にカイ二乗分布の確率変数を簡単に求める方法をこの連載の第7回で紹介しました。自由度n−1をkと表すと、以下のようになります。

　左辺がそれぞれχ1,χ2であれば、

となります。（3）式と（4）式を（1）式に代入してみましょう。

となります。ちゃんと（2）式になっていますね。


コラム　F分布の確率密度関数をシミュレーションで求める

　母分散がσ1,σ2の2つの正規母集団からn1,n2個のサンプルを取り出して不偏分散を求め、上で見た（2）式でF値を繰り返し求めてみましょう。ヒストグラムを作成すると、自由度1がn−1、自由度2がn−2のF分布に従うはずです。

　というわけで、シミュレーションしてみましょう。シミュレーションはExcelでもできますが、多数のセルを使う必要があり、ちょっと面倒です。一応サンプルファイルには作成例（［F分布のシミュレーション］ワークシート）を含めておきますが、ここでは、Pythonのプログラムを使うことにします（リスト1）。

　サンプルプログラムはこちらから参照できます。リンクをクリックすれば、ブラウザが起動し、Google Colaboratoryの画面が表示されます（Googleアカウントでのログインが必要です）。最初のコードセルをクリックし、［Shift］＋［Enter］キーを押してコードを実行してみてください。結果は図7のようになります。コードの詳細については解説しませんが、コメントとリスト1の説明を見れば何をやっているかが大体分かると思います。

# F分布の確率密度関数のシミュレーション
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f

# 正規分布N1（μ=3、σ^2=3）からランダムに10個のサンプルを取り出したものを10000個作る
x1_varp = 3 
x1 = np.random.normal(loc=3, scale=np.sqrt(x1_varp), size=(10000, 10))
# 正規分布N2（μ=4、σ^2=5）からランダムに10個のサンプルを取り出したものを10000個作る
x2_varp = 5 
x2 = np.random.normal(loc=4, scale=np.sqrt(x2_varp), size=(10000, 10))

# サンプルの不偏分散を計算
x1_vars = np.var(x1, axis=1, ddof=1)
x2_vars = np.var(x2, axis=1, ddof=1)

# F値を求める
F = (x1_vars/x1_varp) / (x2_vars/x2_varp)
# ヒストグラムを描く（F値がどのように表れるかが分かる）
plt.hist(F, bins=100, range=(0, 6), density=True) # 階級は100個、縦軸は確率とする

# F分布の確率密度関数を描く
x = np.linspace(0, 6, 100)  # 0〜6までを100個に分けた等差数列（横軸の値）
plt.plot(x, f.pdf(x, 9, 9))  # xに対するF分布の確率密度関数の値をプロットする
plt.show()

リスト1　F分布の確率密度関数をシミュレーションする
正規分布N1（μ＝3, σ2＝3）と正規分布N2（μ＝4, σ2＝5）からランダムにn＝10個の値を取り出すことを10000回繰り返す。10000行×10列のデータが作られるので、各行の不偏分散を求める。10個のデータの不偏分散が10000個作られることになる。この10000個の不偏分散と母分散を基にF値を求める。続いて、縦軸を確率としてF値のヒストグラムを描く。最後に、自由度1＝9、自由度2＝9のF分布の確率密度関数を描けば、ヒストグラムとほぼ重なることが分かる。

　リスト1の実行例が以下の図7です。乱数を使うので結果は毎回少しずつ異なりますが、ほとんど重なっていますね。

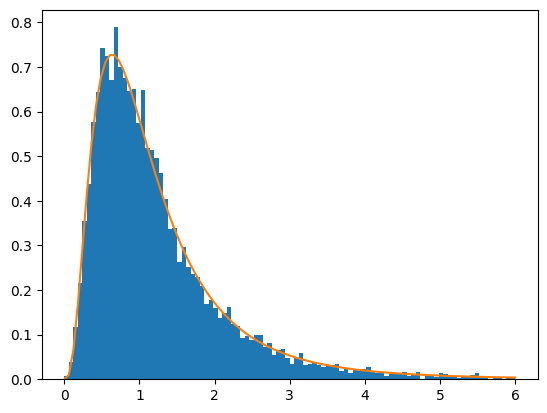
F分布の確率密度関数
図7　F分布の確率密度関数のシミュレーション結果
棒グラフは、2つの正規分布から10個のサンプルを10000回取り出し、それらの不偏分散と母分散を基に求めたF値をヒストグラムにしたもの。折れ線グラフは自由度1＝9、自由度2＝9のF分布の確率密度関数。


コラム　F分布の確率密度関数と累積分布関数を数式で表す

　最初に、F分布の確率密度関数f(x;k1,k2)と累積分布関数F(x;k1,k2)を表す式を掲載しました（確率変数xと自由度k1,k2を;で区切って表記しています）。もう少し詳しく知りたい方のために、定義通りに計算する方法も紹介しておきます。

　ただし、k1,k2は自由度、Izは正則化された不完全ベータ関数で、

とします。

　Γはこの連載で何度も登場したガンマ関数です。ガンマ関数と不完全ベータ関数の定義については、前回紹介したので、そちらを参照していただくこととして、ここでは、Excelの関数を使った計算方法だけを示しておきます。ガンマ関数の値はGAMMA関数で求められ、不完全ベータ関数の値はBETA.DIST関数の累積分布関数で求められます。

　例えば、自由度1が6で、自由度2が10の場合、F＝2に対する確率密度関数の値を（5）式の定義に従って求めたい場合は、k1に6、k2に10、xに2を代入するだけです。分子を

　　=GAMMA((6+10)/2)*(6/10)^(6/2)*2^(6/2-1)

で求め、分母を

　　=GAMMA(6/2)*GAMMA(10/2)*(1+6/10*2)^((6+10)/2)

で求めて割り算すればいいですね。分子は4354.56、分母は26340.42となるので、結果は0.1653となります。一方、累積分布関数の値を（6）式に従って求めたい場合は、BETA.DIST関数にzの値とa＝k1/2, b＝k2/2の値を指定します。従って、

　　=BETA.DIST(6*2/(6*2+10), 6/2, 10/2, TRUE)

と入力します。結果は0.8411となります。サンプルファイルの［F分布（定義通りに）］ワークシートには上のような値ではなく、セルアドレスを指定して0.0〜6.0までの確率密度関数の値と累積分布関数の値を求めた例を含めてあります。もっとも、実用的にはF.DIST関数を使った方が便利ですね。


　今回はF分布の確率変数であるF値の意味やその求め方、さらに、F分布の確率密度関数と累積分布関数の求め方などについてお話ししました。推測統計編の内容についても、かなり踏み込んでお話ししてしまいました。F分布は、母分散の比の区間推定や等分散の検定などに使われますが、ここでは、F分布の確率変数と確率密度関数、累積分布関数についての理解を深めていただければ十分かと思います。

　次回は一定時間内に何らかの事象が起こる確率を求める場合などに使われる指数分布についてお話しします。次回もお楽しみに！

この記事で取り上げた関数の形式

　関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。

F分布の確率密度関数や累積分布関数の値を求めるための関数

F.DIST関数：F分布の確率密度関数や累積分布関数の値を求める

形式

F.DIST(x, 自由度1, 自由度2, 関数形式)

引数

  • x： 確率変数の値（F値）を指定する。
  • 自由度1： 自由度1を指定する。
  • 自由度2： 自由度2を指定する。
  • 関数形式： 以下の値を指定する。
    • FALSE …… 確率密度関数の値を求める
    • TRUE …… 累積分布関数の値を求める

備考

※累積分布関数の値は左側確率（または下側確率）とも呼ばれます。


F.DIST.RT関数： F分布の右側確率の値を求める

形式

T.DIST.RT(x, 自由度1, 自由度2)

引数

  • x： 確率変数の値（F値）を指定する。
  • 自由度1： 自由度1を指定する。
  • 自由度2： 自由度2を指定する。

備考

※1から、F.DIST関数で求められる累積分布関数の値を引いた値が返されます。


F分布の累積分布関数に対する逆関数の値を求めるための関数

F.INV関数： F分布の累積分布関数に対する逆関数の値を求める

形式

F.INV(累積確率, 自由度1, 自由度2)

引数

  • 累積確率： 累積分布関数の値を指定する。
  • 自由度1： 自由度1を指定する。
  • 自由度2： 自由度2を指定する。

備考

※累積確率には左側確率の値を指定します。右側確率に対する逆関数の値を求めたいときには、F.INV.RT関数を使うか、1−右側確率を指定します。


F.INV.RT関数： F分布の右側確率に対する逆関数の値を求める

形式

F.INV.RT(右側確率, 自由度1, 自由度2)

引数

  • 右側確率： 累積分布関数の右側確率の値を指定する。
  • 自由度1： 自由度1を指定する。
  • 自由度2： 自由度2を指定する。

備考

※例えば、右側確率が5%の場合のF値は、F.INV関数で左側確率を95%と指定した場合のF値と一致します。


「やさしい確率分布」のインデックス

「やさしい確率分布」

Copyright© Digital Advantage Corp. All Rights Reserved.

[an error occurred while processing this directive]
ページトップに戻る