[pandas超入門]正規化と標準化についてもうちょっと:Pythonデータ処理入門
正規化と標準化はデータセットのスケーリングに大いに役立ちますが、今回は実際にどんなふうにスケーリングが行われるかについてちょっと見てみましょう。
本シリーズと本連載について
本シリーズ「Pythonデータ処理入門」は、Pythonの基礎をマスターした人を対象に以下のような、Pythonを使ってデータを処理しようというときに便利に使えるツールやライブラリ、フレームワークの使い方の基礎を説明するものです。
- NumPy(「NumPy超入門」の目次はこちら)
- pandas(本連載)
- Matplotlib
なお、本連載では以下のバージョンを使用しています。
- Python 3.12
- pandas 2.2.1
前回はデータをスケーリングしてみようということで、正規化(Min-Max Normalization)と標準化(Standardization)を行う2つの関数をPythonで定義してみました。今回はこれらの関数を再び使って、正規化と標準化についてもう少し詳しく見てみることにしましょう。その前にpandasとNumPyをインポートしておきます(今回はサンプルのデータセットを作成するのにNumPyを使用するため)。それからデータの視覚化を行うツールとしてMatplotlibもインポートしておくことにします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
サンプルのデータセットの作成
ここでは一様分布に従うデータと、正規分布に従うデータの2種類のデータを作成し、それらをDataFrameオブジェクトにまとめます。そのためのコードを以下に示します。
num_of_data = 1000
np.random.seed(8)
uniform_data = np.random.uniform(0, 20, num_of_data)
normal_data = np.random.normal(50, 30, num_of_data)
df = pd.DataFrame({'uniform': uniform_data, 'normal': normal_data})
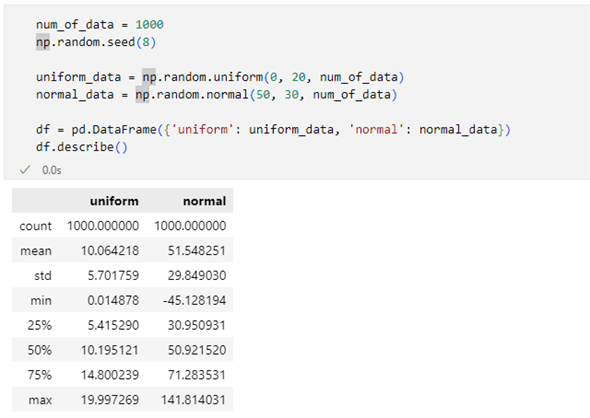
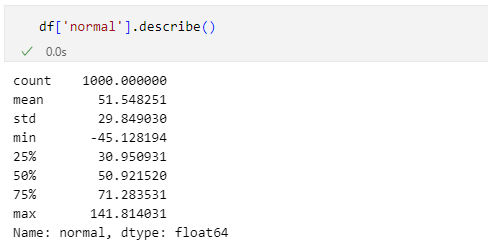
df.describe()
ここでは乱数のシードを8に固定しています。また、一様分布しているデータはnumpy.random.uniform関数で、正規分布しているデータはnumpy.random.normal関数で作成しました。
numpy.random.uniform関数にはデータの最小値に0を、最大値に20を、データの個数にnum_of_data=1000を指定しています。numpy.random.normal関数には平均値に50を、標準偏差に30を、データの個数にnum_of_data=1000を指定しています。
このコードをVisual Studio Code(以下、VS Code)で実行した結果は以下の通りです。
「df.describe()」の実行結果を見ると、一様分布のデータは最小値がだいたい0で、最大値が約20、平均は約10になっていることが分かります(numpy.random.uniform関数の呼び出しでそのように指定したので当たり前といえば当たり前です)。平均値が約10であることからも、これが0から20の範囲で一様に分布していることが想像できます。一方、正規分布のデータは平均が約50、標準標準が約30とこちらも上のコードで指定した通りのデータが作られているようです。
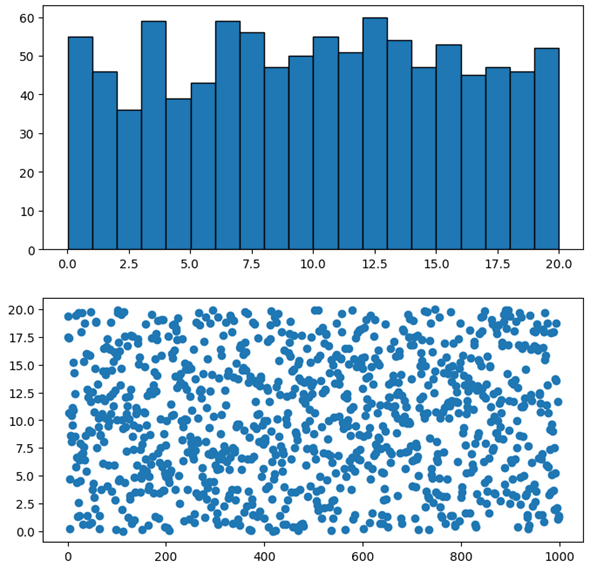
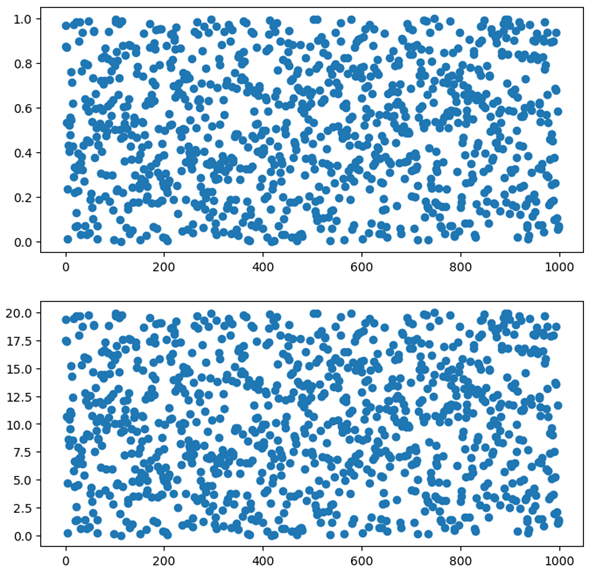
次にこれらをMatplotlibで可視化してみましょう。細かい設定はせずに、単にヒストグラムと散布図を描くだけとします。まずは一様分布のデータのヒストグラムと散布図を描いてみましょう。ここではヒストグラムは20個の区画(ビン)に区切るようにして、散布図の横軸には行インデックスを、縦軸にはその行にある一様分布のデータの値を指定することにしました。
plt.rcParams['figure.figsize'] = (8, 8) # 大きさ調整
plt.subplot(211) # 2行1列の1番目にヒストグラム
plt.hist(df['uniform'], bins=20, edgecolor='black')
plt.subplot(212) # 2行1列の2番目に散布図
plt.scatter(range(num_of_data), df['uniform'])
plt.show()
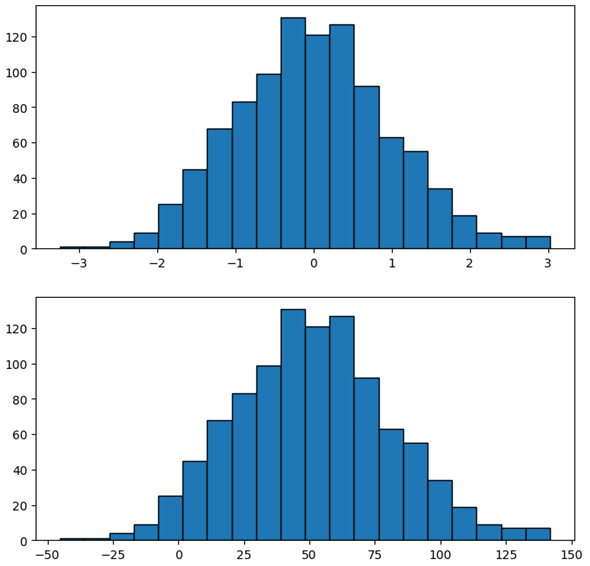
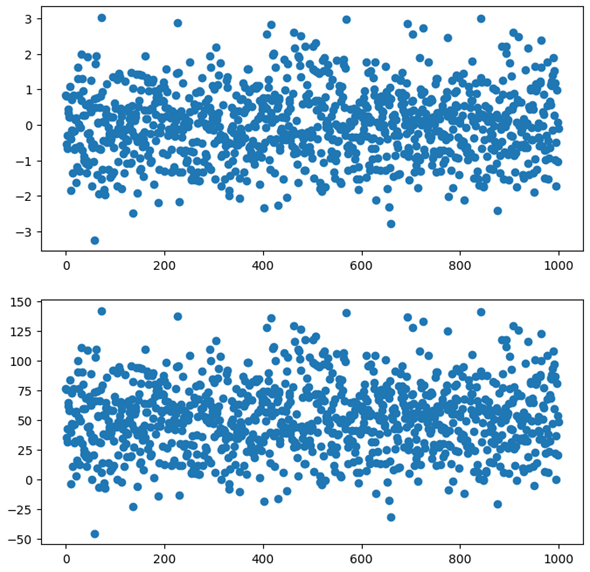
VS Codeでこのコードを実行すると以下のようになりました。
ヒストグラムを見ると、それなりのばらつきがあるものの、全体の形状はある程度平たんになっているといえます(次に見る正規分布と比べてみてください)。また、散布図を見ると、横軸の行インデックスに沿って縦軸の値がランダムに散らばっていることが分かります。これは指定した最小値と最大値の範囲で一様分布に従ってデータがランダムに作成されているからです。
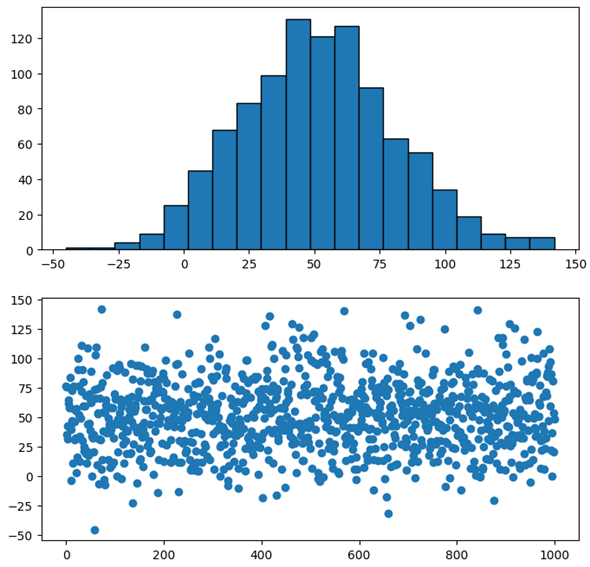
正規分布のデータでも同じことをしてみます。
plt.subplot(211)
plt.hist(df['normal'], bins=20, edgecolor='black')
plt.subplot(212)
plt.scatter(range(num_of_data), df['normal'])
plt.show()
実行結果を以下に示します。
ヒストグラムは一目瞭然で平均値として指定した50近辺のデータ数が一番多く、そこからなだらかに下っていく形状になっています。また、散布図を見ると、やはり平均値である縦軸の50の近辺ではデータが密集し、上下方向に向かっていくに連れてデータがまばらになっていることが分かります。
以下では正規化と標準化でデータがどのようにスケーリングされるかを見ていきますが、その前に基本的な特徴を以下にまとめておきます。
| 手法 | 概要 | 説明 |
|---|---|---|
| 正規化(Min-Max Normalization) | 0から1の範囲に収まるようにデータをスケーリング | 最大値/最小値の範囲が明確な場合に有用。ただし、外れ値の影響を受けやすい |
| 標準化 | 平均0、標準偏差1となるようにデータをスケーリング | 正規分布しているデータのスケーリングに適しているが、正規分布していないものでもスケーリングは可能。正規化が適していない場面で標準化が役立つことがある |
| 正規化と標準化 | ||
正規化してみる
これらのデータをMin-Max Normalizationで正規化してみるとどうなるでしょう(ここでは一様分布している列をMin-Max Normalizationしていますが、一様分布のデータを標準化してはいけないというものでもありません。後述)。Min-Max Normalizationを行う関数は以下のようなものでした。
def min_max_normalize(x):
x_min = x.min()
x_max = x.max()
return (x - x_min) / (x_max - x_min)
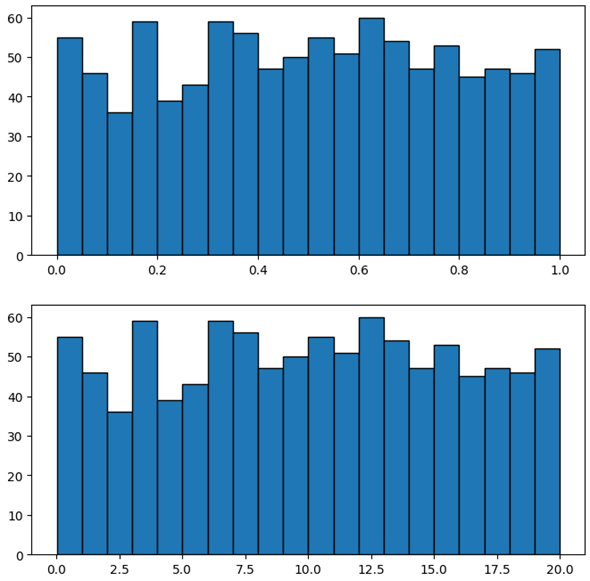
この関数に一様分布しているデータを渡して、その戻り値を'normalized_uniform'列のデータとして元のDataFrameオブジェクトに格納し、そのヒストグラムを表示するのが以下のコードです(比較用に元の'uniform'列のデータのヒストグラムも描画しています)。
df['normalized_uniform'] = min_max_normalize(df['uniform'])
plt.subplot(211)
plt.hist(df['normalized_uniform'], bins=20, edgecolor='black')
plt.subplot(212)
plt.hist(df['uniform'], bins=20, edgecolor='black')
plt.show()
実行結果を以下に示します。
ご覧の通り、全体の形状は何も変わっていません。ただし、横軸の目盛りが上のヒストグラム(正規化後)では0.0から1.0になっています(正規化前の下のヒストグラムでは0.0から20.0まで)。
散布図についても同様です。
plt.subplot(211)
plt.scatter(range(num_of_data), df['normalized_uniform'])
plt.subplot(212)
plt.scatter(range(num_of_data), df['uniform'])
plt.show()
実行結果を以下に示します。
散布図では横軸は行インデックスなことに変わりはありません。ただし、正規化後の縦軸に目を向けると先ほどと同様、全体の形状はそのままで0.0から1.0までの範囲に含められるようになっています。
これまでは一様分布の列を1つだけ取り扱っていましたが、ここで一様分布のデータが2列あるデータセットを考えてみましょう。
n = 100
np.random.seed(42)
row1 = np.random.uniform(0, 30, n)
row2 = np.random.uniform(0, 5, n)
df2 = pd.DataFrame({'row1': row1, 'row2': row2})
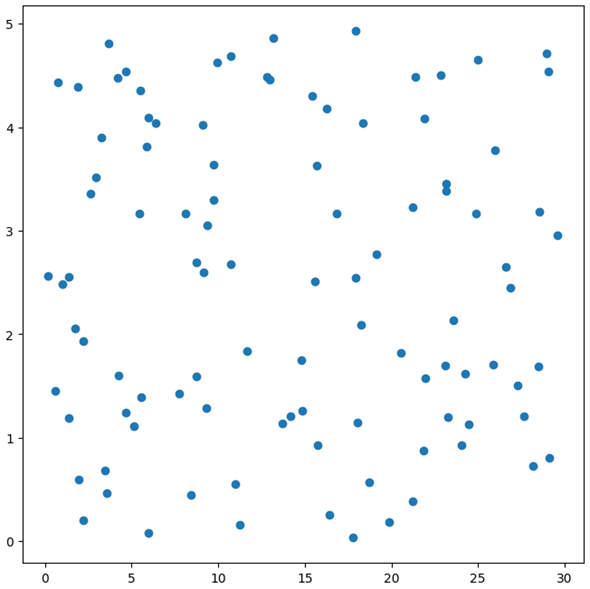
plt.scatter(df2['row1'], df2['row2'])
plt.show()
このデータセットでは、'row1'列と'row2'列の2つの要素で1件のデータを表していると考えられます。そして、これらの値を横軸と縦軸に取ることで2次元のグラフに散布図としてプロットしたのが以下です。
縦軸と横軸の目盛りが異なる範囲になっている点には注意してください(0から30と、0から5)。これを正規化し、散布図としてグラフにプロットしてみましょう。
df2['normalized_row1'] = min_max_normalize(df2['row1'])
df2['normalized_row2'] = min_max_normalize(df2['row2'])
# plt.scatter(df2['row1'], df2['row2'])
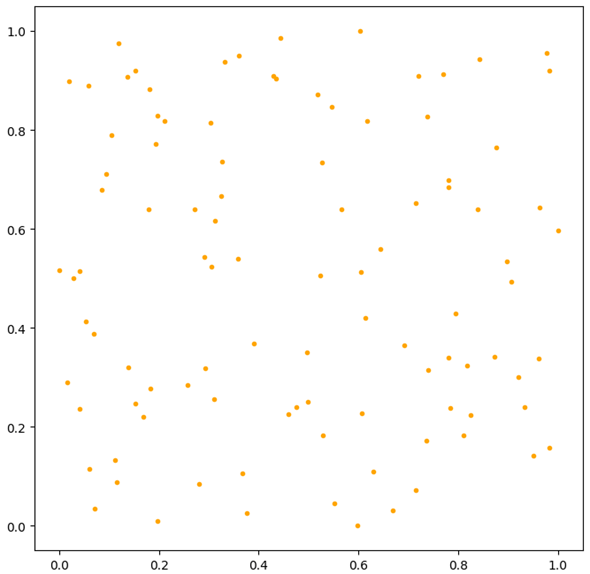
plt.scatter(df2['normalized_row1'], df2['normalized_row2'], marker='.', color='orange')
plt.show()
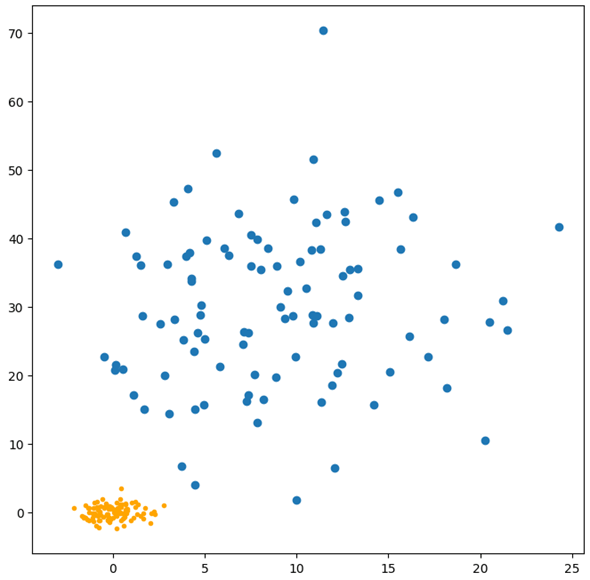
実際にプロットしたものを以下に示します。
今度は縦軸も横軸も同じスケールになりましたが、プロットされたものの形状は先ほどと変わりありません(特徴量が持つ基本的な性質は変わらないということです)。複数の列(特徴量)からなるデータセットにおいて、どれかの列の値だけが他の列と比べてとても大きいと、そのデータセットを使って機械学習なりディープラーニングなりをしようとしたときに、値が大きい列がことさら重要視されてしまうかもしれません。スケーリングはそのような偏りをなくして、全ての列が平等に取り扱えるようにするためのものです。加えて、スケーリングによってデータセット内の数値を一定範囲に収めることで、アルゴリズムの性能が向上することもあります。
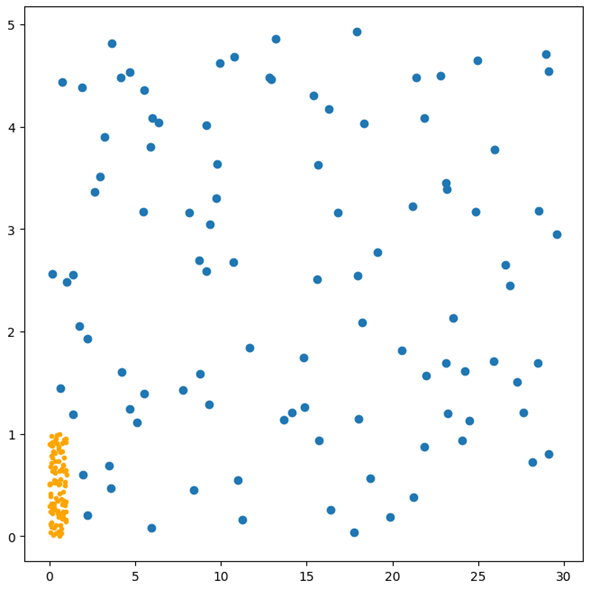
なお、上のコードにあるコメントアウトしている行を有効にして、散布図をプロットすると次のようになります。
元の散布図もプロットしているので、縦軸と横軸のスケールが均等でなくなってしまっていますが、よく見るとオレンジ色の点(正規化後のデータ)は0から1の範囲に含まれていて、なおかつ元データと似た形状になっていることが分かるでしょう。
標準化してみる
正規化は正規分布しているデータのスケーリングに向いています(が、一様分布のデータを標準化することもあります)。ここでは最初に作ったDataFrameオブジェクトであるdfの'normal'列を正規化してみましょう。ただし、その前にdescribeメソッドで'normal'列の概要を再確認しておきます。
平均が約50、最小値が-45くらい、最大値が141くらい、標準偏差が30くらいになっています。
前回に定義した正規化(Standardization)を行う関数は次のようなものでした。
def standardize(x):
std = x.std()
mean = x.mean()
return (x - mean) / std
この関数に'normal'列のデータを与えて、標準化の前と後のヒストグラムをプロットするコードを以下に示します。
df['standardized_normal'] = standardize(df['normal'])
plt.subplot(211)
plt.hist(df['standardized_normal'], bins=20, edgecolor='black')
plt.subplot(212)
plt.hist(df['normal'], bins=20, edgecolor='black')
plt.show()
実行結果は次の通りです。
先ほどと同様、ヒストグラムの形状に変わりはありませんが、横軸の目盛りは変わっている点に注目です。中央は平均値の0、そこから±3程度の範囲にほとんどのデータが含まれます(ここでは平均が0で、標準偏差が1になるように標準化していたことを思い出してください。そのため、3σ=3となります。正規分布では平均±3σの範囲にほぼ全ての数値が収まります)。
散布図についても同様です。
df['standardized_normal'] = standardize(df['normal'])
plt.subplot(211)
plt.scatter(range(num_of_data), df['standardized_normal'])
plt.subplot(212)
plt.scatter(range(num_of_data), df['normal'])
plt.show()
実行結果を以下に示します。
こちらも縦軸の目盛りが-3から3の範囲にデータセットの数値が収まるようになっています。
先ほどと同様に、正規分布している2列のデータを作成し、それらを標準化する前と後の散布図もプロットしてみましょう。
n = 100
np.random.seed(84)
row1 = np.random.normal(10, 5, n)
row2 = np.random.normal(30, 10, n)
df3 = pd.DataFrame({'row1': row1, 'row2': row2})
df3['standardized_row1'] = standardize(df3['row1'])
df3['standardized_row2'] = standardize(df3['row2'])
plt.scatter(df3['row1'], df3['row2'])
plt.scatter(df3['standardized_row1'], df3['standardized_row2'], marker='.', color='orange')
plt.show()
こちらも縦軸と横軸のスケールが異なるために、少し潰れたような形になっていますが、元データの形状はそのままに原点(平均)の周囲に各値が移動したことが分かります。
一様分布の列を標準化してみる
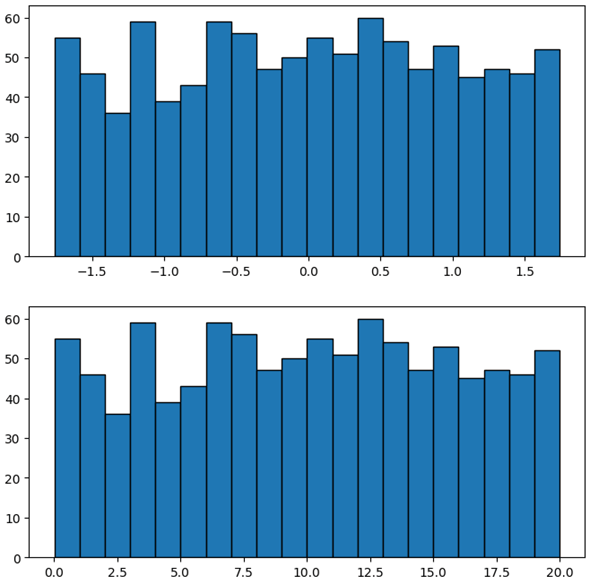
最後に一様分布している列を標準化してみましょう。ここでは簡単に標準化後の列の概要とヒストグラムだけを示します。
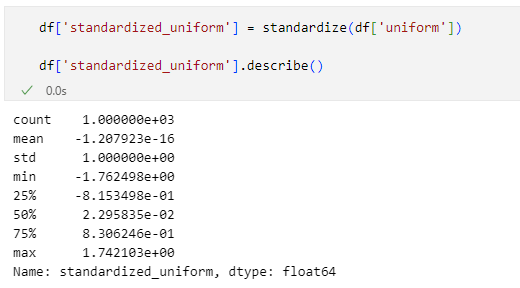
df['standardized_uniform'] = standardize(df['uniform'])
print(df['standardized_uniform'].describe())
実行結果は次の通りです。
最小値と最大値がどちらも2σよりも小さな範囲に収まっています(これには根拠がありますが、ここでは紹介しません。おおよその最小値は-1.73程度、最大値は1.73程度になります)。そのため、ヒストグラムもその範囲にデータが収まるようになっています。
plt.subplot(211)
plt.hist(df['standardized_uniform'], bins=20, edgecolor='black')
plt.subplot(212)
plt.hist(df['uniform'], bins=20, edgecolor='black')
plt.show()
実行結果は以下の通りです。
ここでは示しませんが、正規分布のデータを正規化(Min-Max Normalization)することも可能です。
正規化と外れ値
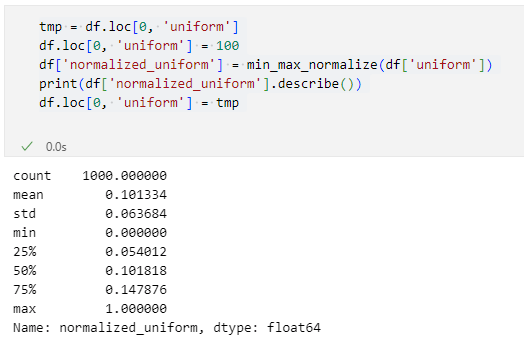
本稿の頭の方で正規化は外れ値の影響を受けやすいとしましたが、実際に例を見てみましょう。
tmp = df.loc[0, 'uniform']
df.loc[0, 'uniform'] = 100
df['normalized_uniform'] = min_max_normalize(df['uniform'])
print(df['normalized_uniform'].describe())
df.loc[0, 'uniform'] = tmp
このコードはわざと外れ値をデータセットに含めた上で、正規化(Min-Max Normalization)をしているコードです。正規化によってできた'normalized_uniform'列の概要を確認してみましょう。元の列は0から20の範囲に含まれる数値を格納していたのですが、そこに100という外れ値を1つ入れた結果が以下です。
正規化により0から1の範囲にスケーリングが行われました。ここで、元々の外れ値(最大値)は100でしたが、それが1にスケーリングされたということです。そして、他の値は最大でも20がいいところです。そのため、外れ値以外の値が相対的に小さくなりすぎて、75パーセンタイルの値ですら0.14と極めて小さな値になってしまっています。
外れ値の影響を低減するために四分位数を使う方法などがありますが、ここでは説明はしないことにします。
実際にスケーリングの手法として何を使うかは手元にあるデータセットとご相談、ご検討の上で決めるしかないでしょう。本稿ではこんなふうにスケーリングされているんだよ、というところで話を止めておきます。
というわけで、次回は連載のまとめとして何かしてみたいと考えていますが、まだ決まっていません(笑)。
Copyright© Digital Advantage Corp. All Rights Reserved.