テラリウム徹底攻略ガイド（改訂版） 障害物回避のためのアルゴリズム 泉 祐介＋デジタルアドバンテージ 2003/05/10

---

　それでは、障害物回避のアルゴリズムについて考えていこう。まず、自分の現在地と目的地を直線で結ぶ。このとき、障害領域と交わることがなければ、そのまま直線経路で目的地に向かえばよいことになる。例えば、下図の左側のような場合は、単純に直線経路で移動することができる。一方、右側のような場合は、直線経路で移動しようとすると、障害物に衝突してしまう。

直線経路で移動できる場合とできない場合

左側のような場合は直線経路で目的地に到達できるが、右側のような場合は直線経路では目的地に到達できない。

　上図の右側のように、直線経路上にいくつかの障害領域が存在する場合もあるが、このような場合は一番近くにある障害領域を避けて通ることを考える。もちろん、一番近くにある障害物だけをよけられればよいというわけではないが、障害物をよけている間にも周囲の状況は絶えず変化する。例えば、遠くにある障害物が動物であれば、こちらが目の前にある障害物をよけて移動している間にほかの場所に移動しているかもしれない。また、障害物が植物であっても、動物に食べ尽くされるなどしてなくなっているかもしれない。そのため、先々を見越して目的地までの経路を探索しても、すぐに無駄になる可能性は大きい。従って、取りあえず今回はすぐ近くにある障害物をよけることに専念し、遠くの障害物は近くの障害物をよけてから処理することにした。しばらくは一番近くにある障害領域だけを考え、ほかの障害領域はないものとしよう。

　さて、この障害領域を避けるには適当な点を経由していくことになるわけだが、一般的に考えれば、障害領域の角のいずれかということになる。障害領域の角は4点存在するが、まずは目的地と障害領域との位置関係によって候補を2つの角に絞る。

■経由点の候補となる2つの角

　障害領域の真上、真下、真左、真右、つまり下図のに当たる領域内に目的地があるときは、目的地に直接移動できる角は2点しかない。ここでは目的地が真上にある場合を例として図に示した。このようなときは、この2点を経由点の候補とする。

　一方、障害領域の左上、右上、左下、右下、つまり下の図のに当たる領域内に目的地があるときは、目的地に直接移動できる角が3点ある。目的地が障害物の右上にあるような場合を例として図に示した。このようなときは、目的地から一番近くにある角を除いた2点を経由点とする。

障害物をよけるために経由する点

に当たる領域に目的地がある場合は、目的地に直接移動できる角は2点しかない。一方、に当たる領域に目的地がある場合は、目的地に直接移動できる角は3点ある。

　上図のに当たる領域に目的地があるときに一番近くにある角を候補から除くのは、その点を経由するのは意味がないからである。例えば、やはり目的地が障害領域の右上にある場合で考えると、一番近くの角となるのは障害領域の右上の点である。そこで、この右上の点に直接移動できる領域を考えると、下図のグリーンで示した領域になる。ところが、図を見れば分かるとおり、グリーンで示した領域からは目的地にも直接移動できる。結局、目的地から一番近くにある角を経由する意味はまったくないことが分かる。

目的地の一番近くの角に直接到達できる領域

目的地から一番近い右上の角に直接移動できるのは、グリーンで示した領域である。ところが、図を見れば分かるが、グリーンで示した領域からであれば目的地に直接到達できる。

■経由点の決定

　さて、ここまでで経由点の候補を2つに絞ったが、この候補は自分がいる位置をまったく考えずに決めているため、経由点にも直接移動できるとは限らない。例えば、下の図でいえば、右下の点には直接移動することができるが、左上の点には直接移動することができない。このような場合は、この例の右下の点のように、いま自分がいる点から直接移動できる点を選んだ方がよいのはいうまでもない。

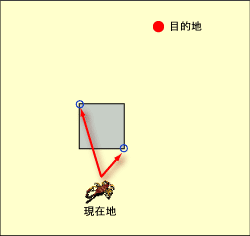経由点に直接移動できる場合とできない場合

右下の点には直線経路で到達することができるが、左上の点には直線経路では到達できない。

　上の図のように、候補のうち少なくとも1つが直接移動することができる場合は、2つに絞った候補のうち、自分がいる点から見て、距離が近い方の点を経由するようにすれば、必ず直接移動できる方の点を経由することになる（詳しいことは省略するが、興味のある読者は確かめてみて欲しい）。そのため、候補を2つにしぼったあとは、その候補となった点のうち距離が近い方の点を経由するようにする。

　ただし、実際にはどちらの点も直線経路では移動できない場合もある。下図の左のような場合が典型的な例である。また、図の右のように、経路を変更したことによってこれまで考えていなかった別の障害領域が移動の妨げになることもある。

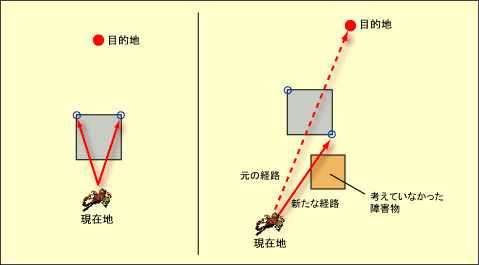いずれの候補にも直接移動できない場合

左のように、候補となった点がいずれも現在地からは直接移動することができない場合がある。また、右のように、新たに通行の妨げとなるような障害領域が生じる場合もある。

　この問題は同じ考え方を再帰的に適用することによって解決する。つまり、いま決めた経由点を新たな目的地として、これまでに説明してきたアルゴリズムを繰り返し実行するのである。これによって最終的には直線経路で到達できる適当な経由点を見つけることができる。

■経由点の修正

　ところで、一番近くにある障害領域だけを考えてアルゴリズムを決めたわけだが、1つ問題がある。障害物と障害物の間隔が狭い場合、障害物のまわりに設けた通行できない部分が重なることもあると先に述べた。これは、障害領域が重なることを意味する。つまり、経由点の候補として挙げた障害領域の角が、ほかの障害領域に含まれることもあり得るのである。例えば、下の図のような場合がこれに当たる。

経由点の候補が障害領域に含まれる場合

障害領域（下側）の左上の点がすぐ左上にある障害領域に含まれているため、この点を経由するのは不可能である。

　この場合、経由する点をほかの適当な点に変える必要がある。その点を候補から切り捨てて候補の数を減らすこともできるが、候補となっている2点がともに何らかの障害領域に含まれている状況になると、候補がなくなってしまう。そこで、下図のように、経由点を含んでいる領域の角に経由点を変更する。例えば、先に示した図のような場合は、左上隅がその左上にある領域に含まれているので、その左上の領域の左上隅を新しい候補とする。

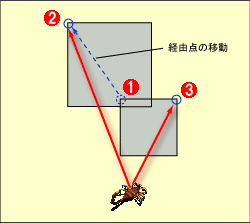経由点の変更

この図のような場合、経由点の候補であるが左上の領域に含まれているので、に候補を変更する。このともう1つの候補であるとで距離を比べると、のほうが近いため、最終的にはこの点を経由点として決定する。

　なお、この候補の変更は、最終的に距離の近い方の候補を経由点として決める前に行う。多くの場合、候補を変更すれば経由する点はより遠くなって、移動に時間がかかるようになってしまうためだ。

INDEX
	テラリウム徹底攻略ガイド （改訂版）
	第6回 より高度な障害物回避
	障害物の扱い方
	障害物回避のためのアルゴリズム
	障害物回避アルゴリズムの実装
	KAnimalクラスにあるメソッドのオーバーライド

　

「テラリウム徹底攻略ガイド（改訂版）」

＠ITメールマガジン　新着情報やスタッフのコラムがメールで届きます（無料）