第3回　複雑なものを単純に〜分類と分解〜


河合昭男
（有）オブジェクトデザイン研究所

2002/12/12

---

　前回は、「オブジェクトに必要な4つの特性とは？」と題して、カプセル化、オブジェクトの特性、クラスとインスタンスについて解説しました。オブジェクトは、状態と振る舞いがカプセル化されており、外部からコミュニケーションするには、公開されているインターフェイスを経由しなければなりません。それ以外の方法で、直接内部の状態をアクセスすることはできないのです。また、オブジェクトは状態（属性）、振る舞い（操作）、ほかのオブジェクトとの関係、オブジェクトであると識別可能なアイデンティティという4つの特性を持つ、というのが前回の内容でした。今回は「分類と分解」をテーマに、クラス階層と複合オブジェクト、ポリモフィズム、パワータイプについて身近な例を挙げながら解説します。

---

クラス階層

【クラスを分類する】

　クラスは、その意味や属性、操作の差異に注目して分類することができます。分類されたクラスを元のクラスのサブクラス、元のクラスをスーパークラスと呼びます

【is-aの関係】

　クラスとサブクラスの関係をis-a関係と呼ぶことがあります。その理由は、サブクラスはスーパークラスの一種なので「サブクラス is-a スーパークラス」という表現方法が自然にできるからです。「A is-a B」かつ「B is-a C」ならば「A is-a C」なので、is-a関係は推移律が成立します。またis-a関係は階層構造を持つことができます。

【クラス階層の例】

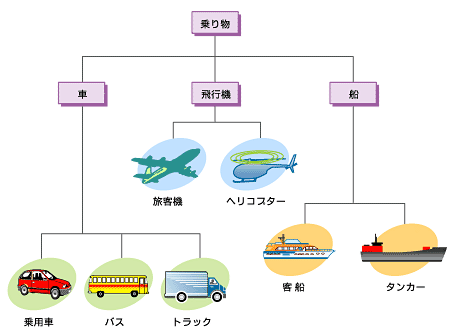
　例えば「乗り物」クラスの分類を考えてみましょう。「乗り物」クラスは、「車」「飛行機」「船」というサブクラスに分類できます。「車is-a乗り物」、つまり車は乗り物の一種です。飛行機、船も同様です。「車」クラスはさらに、「乗用車」「バス」「トラック」というサブクラスに分類できます。「乗用車is-a車」、つまり乗用車は車の一種です。バス、トラックも同様です（図1）。　

図1 クラス階層−乗り物の分類

【サブクラスと部分集合】

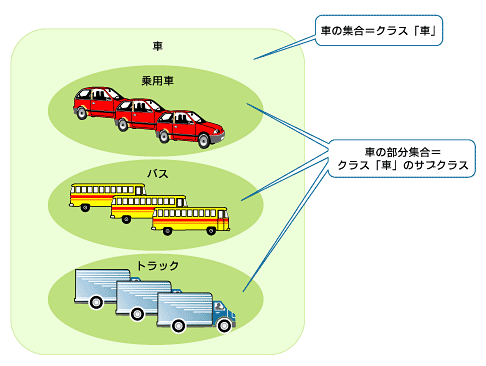
　クラスは集合と考えることができる、と前回解説しましたが、サブクラスは部分集合と考えることができます。例えば、車クラスを次のように乗用車10台、バス10台、トラック10台からなるオブジェクトの集合と考えます。

　車＝｛乗用車1、……、乗用車10、バス1、……、バス10、トラック1、……、トラック10｝。

　ここで乗用車n、バスn、トラックnは、駐車場に駐車しているというような具体的な車を示します。この集合を次の3つの部分集合に分割します。

乗用車	｛乗用車1、……、乗用車10｝
バス	｛バス1、……、バス10｝
トラック	｛トラック1、……、トラック10｝

　以上はそれぞれ、車クラスのサブクラスです。集合論で使用する包含関係「⊃」で表すと、

車⊃乗用車

車⊃バス

車⊃トラック

となります。このようにクラスとサブクラスの関係は、集合と部分集合としてとらえることができます（図2）。

図2 サブクラスと部分集合

複合オブジェクト

【部分と全体】

　あるオブジェクトが、その部品となるオブジェクトで全体を構成しているとき、そのようなオブジェクトを複合オブジェクトと呼びます。

【分類と分解】

　複雑なものを理解するためには、分類して整理する方法と、単純なものに分解する方法があります。サブクラスという概念は、クラスを分類して整理する手法です。一方、複合オブジェクトという概念は、複雑なオブジェクトを単純なオブジェクトに分解する手法と考えられます。分類はクラスという抽象概念を対象にしていますが、分解はクラスではなく具体的なオブジェクトを対象としているという違いもあります。

【part-ofの関係】

　複合オブジェクトとそれを構成する部品オブジェクトとの関係をpart-of関係と呼ぶことがあります。部分は全体の一部なので「部分はpart-of全体」という表現方法が自然にできるからです。

　「Aはpart-of B」かつ「Bはpart-of C」ならば「A はpart-of C」なので、part-of関係は推移律が成立します。またis-a関係と同様、part-of関係も階層構造を持つことができます。この関係はhas-a関係と呼ぶこともあります。この場合、part-of関係と主語が反対になり「全体has-a部分」と表現することができます。全体が部分を保有しているという意味です。

【複合オブジェクトの例】

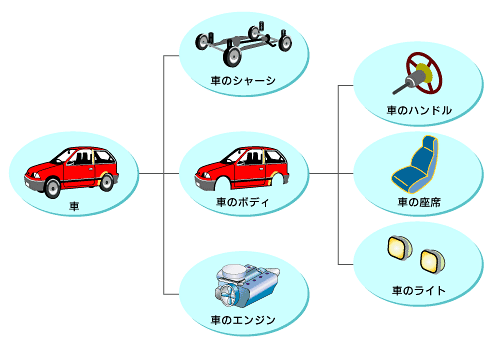
　例えば、車はボディ、シャーシ、エンジンなどさまざまな部品で構成されています。さらに、ボディは運転装置、内装、照明などで構成されています。つまり、車というオブジェクトは複合オブジェクトであり、車を構成する部品自体も、より小さな部品で構成される複合オブジェクトであると考えることができます（図3）。

図3 車を構成する部品自体も、より小さな部品で構成される複合オブジェクトである

ポリモフィズム

【ポリモフィズムとは】

　polymorphismという単語は“poly”＋“morph”＋“ism”に分解できます。“poly”は多くの、“morph”は形、形態です。つまり多くの形態という意味で、多態性または多相性と訳されています。いずれにしてもあまりイメージがわいてきませんね。ポリモフィズムとは、同じ名前の操作が多くの形を取る、異なる振る舞いをする、ということを意味します。

【ポリモフィズムの例】

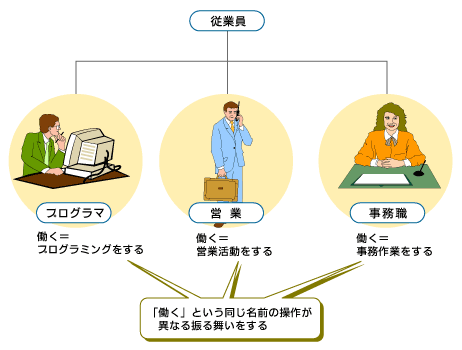
　例えば会社で働いている人を考えます。「仕事をする」「働く」といってもその内容は職種により異なります。プログラマはプログラミングを行い、営業担当は営業活動を行い、事務職は事務作業を行います。

　「従業員」というクラスを分類すると、「プログラマ」「営業担当」「事務職」というサブクラスに分類することができます。各サブクラスは「働く」という同じ名前の操作を持っていますが、その振る舞いはそれぞれのサブシステムに個別に定義されていて異なります。これがポリモフィズムです。

図4 ポリモフィズムの例

パワータイプ

【前回の問題】

　では、前回の最後の問題について考えてみましょう。

楽器というクラスを考えます。楽器にはピアノ、バイオリン、フルート などがありますが、これらは「楽器」クラスのインスタンスでしょうか？

【サブクラスと部分集合】

　1つの考え方は、「ピアノis-a楽器」です。バイオリン、フルートも同様なので、「ピアノ」「バイオリン」「フルート」は、「楽器」クラスのサブクラスと考えることができます。クラス、サブクラスを集合で考えると、例えば、

　楽器＝｛ピアノ1、……、ピアノ10、バイオリン1、……、バイオリン10、フルート1、……、フルート10｝、

と表すことができます。また、

ピアノ	｛ピアノ1、……、ピアノ10｝
バイオリン	｛バイオリン1、……、バイオリン10｝
フルート	｛フルート1、……、フルート10｝

という集合を考えると、ピアノ、バイオリン、フルートはそれぞれ集合「楽器」の部分集合なので、

楽器⊃ピアノ

楽器⊃バイオリン

楽器⊃フルート

という包含関係が成り立ちます。

【メタクラスと族集合】

　一方、「楽器」クラスではなく「楽器の種類」というクラスを考えてみます。ピアノ、バイオリン、フルートはこのクラスのインスタンスです。

　クラスをインスタンスとするクラスを、メタクラスと呼ぶことがあります。「楽器の種類」はメタクラスと考えることができます。

　集合で考えると、楽器の種類＝｛ピアノ、バイオリン、フルート｝になります。

　ある集合Sの部分集合からなる集合をSの族集合と呼ぶことがあります。例えば、ピアノ、バイオリン、フルートは集合「楽器」の部分集合だから、集合「楽器の種類」は「楽器」の族集合と考えることができます。

　クラスと集合の概念の比較を次の表にまとめます。

クラス	集合
インスタンス	要素
サブクラス	部分集合
メタクラス	族集合

　つまりピアノ、バイオリン、フルートはそれぞれ族集合「楽器の種類」の要素なので、

楽器の種類∋ピアノ

楽器の種類∋バイオリン

楽器の種類∋フルート

という帰属関係が成り立ちます。まとめると、集合「楽器」の部分集合が、族集合「楽器の種類」の要素になっています。

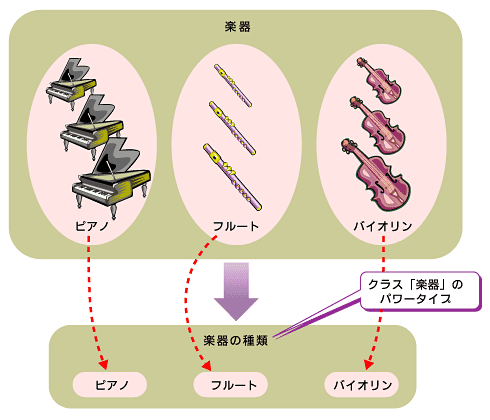
【パワータイプ】

　あるクラスAのサブクラスをインスタンスとするメタクラスPを、クラスAのパワータイプと呼びます。楽器の例だと、メタクラス「楽器の種類」は「楽器」クラスのパワータイプです。冒頭に挙げた車の例でも同様です。メタクラス「車の種類」は「車」クラスのパワータイプです。

図5 パワータイプの例

【次回の予定】

　次回はいよいよ、オブジェクト指向の考え方を、UMLを用いて説明します。

IT Architect 連載記事一覧

---

【参考文献】
『まるごと図解 最新 オブジェクト指向がわかる』、河合昭男、技術評論社
『まるごと図解 最新UMLがわかる』、河合昭男、技術評論社
『ゼロからわかるオブジェクト指向の世界』、岩田裕道＋手島歩三、日刊工業新聞社
『Object-Oriented Methods：A Foundation』、James Martin＋James Odell、Prentice Hall

プロフィール

河合昭男（かわいあきお） 　大阪大学理学部数学科卒業、日本ユニシス株式会社にてメインフレームのOS保守、性能評価の後、PCのGUI系基本ソフト開発、クライアント／サーバシステム開発を通してオブジェクト指向分析・設計に携わる。 　オブジェクト指向の本質を追究すべく1998年に独立後、有限会社オブジェクトデザイン研究所設立、理論と実践を目指し現在に至る。 　事業模型倶楽部、日本XPユーザ会、パターン言語のコミュニティなどソフトウェア新技術の学習と普及を行うコミュニティ活動に参画。著書『まるごと図解 最新オブジェクト指向がわかる』（技術評論社）、『まるごと図解 最新UMLがわかる』（技術評論社）。『UML Press』（技術評論社）、『ソリューションIT』（リックテレコム）ほかの専門誌に多数執筆。ホームページ「オブジェクト指向と哲学」。