検索
連載

データ構造の選択次第で天国と地獄の差：コーディングに役立つ！ アルゴリズムの基本（2）（3/3 ページ）

プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか（編集部）

[山下寛人，オイシックス株式会社] PC用表示 関連情報
Share
Tweet
LINE
Hatena
前のページへ | 　　　　　　

この木何の木、木構造

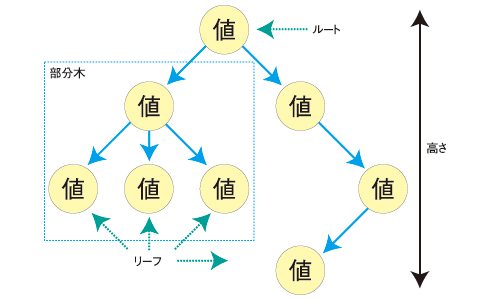
　「木構造（根付き木）」と呼ばれるデータ構造について説明します。リンクリストは直線的にノードがつながっているデータ構造でしたが、木構造は木のような形でノードがつながっているデータ構造です。

  • 木構造はデータを持つノードで構成されています。
  • ノードの中には1つだけルート（根）というノードがあります。図にした場合、一般的に一番上に書かれます。
  • 2つのつながっているノードを見たとき、ルートに近い方を親ノード、ルートから遠い方を子ノードといいます。
  • あるノードの親ノードは1つだけしかありません。子ノードは複数あります。子ノードは1つの場合もあり、1つもない場合もあります。
  • ルートノードには親ノードがありません。親ノードがないのはルートノードだけです。
図4　木構造（根付き木）
図4　木構造（根付き木）
  • 最も末端のノードをリーフ（葉）と呼びます。リーフノードは子ノードを持ちません。
  • ルートから一番下までの階層の数を高さと呼びます。
  • あるノードがルートから何階層にあるかを、そのノードの深さと呼びます。
  • 木構造の中の一部を切り取ったものを部分木と呼びます。
  • ノード同士の関係は親子にちなんで家系のように表現されることがあります。例えば子ノードの子ノードは孫ノード、同じ親を持つノードは兄弟ノード、上の階層のノードは先祖、下流にたどれるノードは子孫、などです。

さまざまな木構造

・順序木

　ノードに順番が付いている木構造を順序木と呼びます。例えば、左上のノードから1番目、2番目、と番号を付けていくような木構造です。ただの木構造の場合、子ノードが右にあっても左にあっても関係ありませんが、順序木の場合は左の子と右の子は区別されます。

図5　順序木
図5　順序木

・二分木

　ノードが子ノードを最大2つしか持たない木構造を二分木と呼びます。左の子と右の子は異なるものとして区別されます。

図6　二分木
図6　二分木

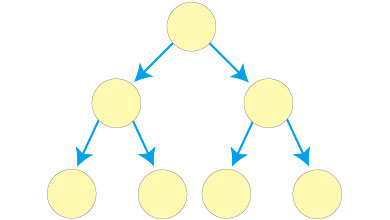
・完全二分木

　すべての葉が同じ深さで、すべての内部の（葉以外の）ノードが2つの子を持つ二分木を完全二分木と呼びます。すべての葉が同じ深さでなくても、左上から順にノードが詰めて位置している場合でも完全二分木と呼ぶこともあります。完全二分木は数値でノードの位置を特定できるため、配列を用いて実装することができます。

図7　完全二分木
図7　完全二分木

・二分探索木

　次のような条件を満たす二分木を二分探索木と呼びます。

  • あるノードの左のノードはそのノード以下の値を持つ。
  • あるノードの右のノードはそのノード以上の値を持つ。
    （以下／以上は未満や超とする場合もあります）

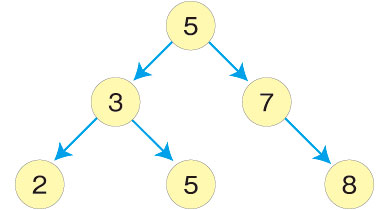
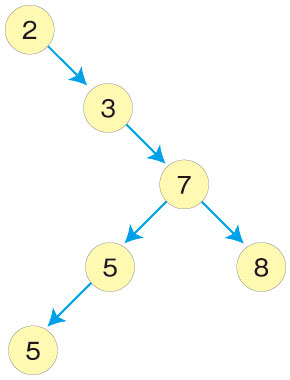
　例を挙げて説明します。

図8　例A
図8　例A

　ルートノードは5、左部分木の2、3、5はいずれも5以下です。右部分木の7、8はいずれも5以上です。木の中のほかのノードも同じ特徴を持っています。例えば「3」のノードは左部分木の2以上で、右部分木の5以下です。

　このようなデータ構造を作っておくことで、特定の値を探索するのに都合がよくなります。

・平衡二分探索木

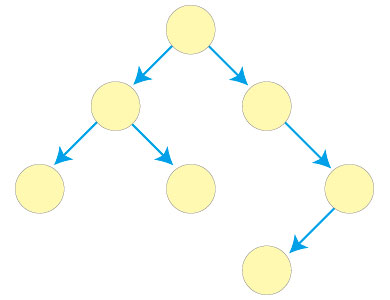
　左右のバランスを取った二分探索木です。つまり右の部分木と左の部分木の高さが最大でも1つしか違わないようにしたものです。例Aは平衡二分探索木ですが、例Bは二分探索木ではあるものの平衡二分探索木ではありません。

　実装は少し難しくなりますが探索の効率はよりよくなります。具体的に探索がどのようになるかは別の機会に解説します。

図9　例B（平衡二分探索木ではない）
図9　例B（平衡二分探索木ではない）

木構造の例：DOMツリー

　木構造になっているデータ構造の身近な例を挙げます。XMLやHTMLはタグで文字列を挟んで記述します。タグの中にはほかのタグを入れることができます。複数のタグを入れることもできますし、さらにその中にタグを入れることもできます。全体として木構造になっています。

　XMLやHTMLをプログラムで扱うためのAPIにDOM（Document Object Model）があります。DOMはXML文書やHTML文書を木構造のオブジェクトに変換することによってプログラムで取り扱えるようにするものです。

　HTMLのタグの木構造を解析するプログラムを作ってみましょう。

<html>
<head>
<script type="text/javascript">
window.onload = function() {
  var str = "";
  var childNodes = document.body.childNodes;
  for (i in childNodes) {
    if (childNodes[i].tagName != undefined) {
      str = str + "―" + childNodes[i].tagName + "<br/>";
      var child = childNodes[i].firstChild;
      while (child != null) {
        if (child.tagName != undefined) {
          str = str + "  ―" + child.tagName + "<br/>"; 
        }
        child = child.nextSibling;
      }
    }
  }
  document.getElementById("output").innerHTML = str;
}
</script> 
</head>
<body>
<p>
<a href="//www.atmarkit.co.jp">＠IT</a> 
</p>
<ul>
<li>1番目</li>
<li>2番目</li>
<li>3番目</li>
</ul>
<hr/>
DOMの解析結果
<br/>
<div id="output"></div>
</body>
</html>
sample2-4.html

　プログラムを解説します。

4行目：

関数を定義しています。HTMLがすべて描画されてから解析を実行しなければならないため、window.onloadとして関数を定義しています。

6行目：

bodyタグの子ノードを取得しています。子ノードは複数存在します。

7行目：

子ノードのそれぞれに対してループします。

8行目：

子ノードのタグ名を取得して、undefinedでないかどうか調べています。DOMの中にはタグでない改行なども含まれるため、タグ名が未定義の場合があります。

9行目：

結果の文字列にタグ名を追加します。

10行目：

子ノードの最初の子ノードを取得します。bodyタグの孫ノードに当たります。

11行目：

子ノードがnullになるまでループします。

12〜14行目：

文字列にタグ名を追加します。孫ノードなので字下げの空白（&nbsp;）を入れています。

15行目：

子ノードの次のノードを取得します。兄弟ノードに当たります。次のノードがない場合はnullになり、ループが終了します。

19行目：

結果を表示します。

　次回は「再帰」というものの解説と、再帰を使ったアルゴリズムを解説します。

著者紹介

山下 寛人

オイシックス株式会社


「次回」へ


「コーディングに役立つ！ アルゴリズムの基本」バックナンバー

Copyright © ITmedia, Inc. All Rights Reserved.

前のページへ | 　　　　　　
ページトップに戻る