再帰でハノイの塔を攻略せよ:コーディングに役立つ! アルゴリズムの基本(3)(2/3 ページ)
プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか(編集部)
フィボナッチ数列のn番目を求める
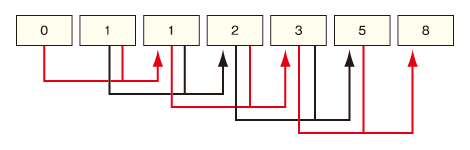
最初は0、次が1、3番目以降は直前の2つの数字を足したものになる数列を、フィボナッチ数列といいます。つまり3番目は0+1=1、4番目は1+1=2、5番目は2+1=3、6番目は2+3=5、といった具合に続いていきます。
この数列のn番目を計算するプログラムを作りましょう。フィボナッチ数列は次のように定義されます。
F0=0
F1=1
Fi=Fi-1+Fi-2 (i≧2)
定義そのものが再帰的になっているので、プログラムもそのまま再帰を使って書くことができます。
<html>
<body>
<script type="text/javascript">
var count = 0;
function startCalc() {
count = 0;
document.getElementById("disp").innerHTML = "";
var number = document.getElementById("number").value;
var start = Number(new Date());
display("disp", number + "のフィボナッチ数=" + fibonacci(number));
var end = Number(new Date());
display("disp", "実行時間:" + (end - start) + "ミリ秒");
display("disp", "計算回数:" + count);
}
function fibonacci(n) {
if (n < 1) {
return 0;
}
if (n == 1) {
return 1;
}
count++;
return fibonacci(n - 1) + fibonacci(n - 2);
}
function display(id, str) {
var element = document.getElementById(id);
element.innerHTML += str + "<br/>";
}
</script>
<input type="text" id="number">
番目のフィボナッチ数を計算する
<input type="submit" value="計算開始" onclick="startCalc()">
<div id="disp"></div>
</body>
</html>
4行目
加算の回数をカウントするための変数countを定義しています。
5行目
画面のボタンをクリックするとstartCalc関数が呼ばれ、計算が始まります。
7行目
2回目以降の実行の際には、前の結果が表示されているので消去します。
8行目
画面のテキストボックスに入力された数値を取得しています。
10行目
フィボナッチ数を計算し、結果を表示します。
15行目
フィボナッチ数を計算するfibonacci関数を定義します。
16〜18行目
0番目のフィボナッチ数は0なので、0を返します。
19〜21行目
1番目のフィボナッチ数は1なので、1を返します。
23行目
2番目以上の場合は1つ前と2つ前のフィボナッチ数の合計を返します。
このプログラムの実行には注意してください。25以上の数を入れて計算させると極端に時間がかかります。1ずつ増やして実行してみてください。数が1増えただけで計算時間が加速度的に長くなっていきます。いまどきのPCは劇的に性能がよくなっているのに、たかだか28や29のフィボナッチ数の計算も精一杯です。
フィボナッチ計算アルゴリズムの改善
計算に時間がかかってしまうのはアルゴリズムがよくないからです。
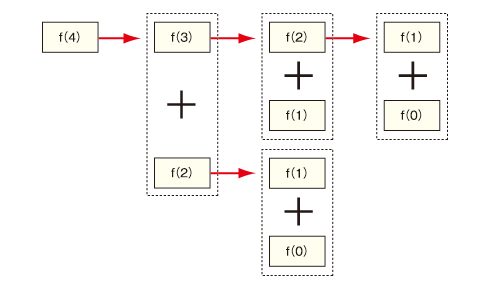
例えば4のフィボナッチ数の計算がどうなるかを考えてみましょう。f(4)が4のフィボナッチ数を表しているとします。
f(2)が2回、全く同じ計算がされていることが分かると思います。数が大きくなれば大きくなるほど同じ計算を行う回数が飛躍的に増えてしまいます。
これを改善するために1度計算した計算結果を覚えておくようにしましょう。改善したプログラムは以下になります。
<html>
<body>
<script type="text/javascript">
var fibonacciResult = new Array();
var count = 0;
function startCalc() {
count = 0;
fibonacciResult = new Array();
fibonacciResult[0] = 0;
fibonacciResult[1] = 1;
document.getElementById("disp").innerHTML = "";
var number = document.getElementById("number").value;
var start = Number(new Date());
display("disp", number + "のフィボナッチ数=" + fibonacci(number));
var end = Number(new Date());
display("disp", "実行時間:" + (end - start) + "ミリ秒");
display("disp", "計算回数:" + count);
}
function fibonacci(n) {
if (fibonacciResult[n] == undefined) {
count++;
fibonacciResult[n] = fibonacci(n - 1) + fibonacci(n - 2);
}
return fibonacciResult[n];
}
function display(id, str) {
var element = document.getElementById(id);
element.innerHTML += str + "<br/>";
}
</script>
<input type="text" id="number">
番目のフィボナッチ数を計算する
<input type="submit" value="計算開始" onclick="startCalc()">
<div id="disp"></div>
</body>
</html>
先ほどのプログラムとの違いを説明します。
4行目
n番目のフィボナッチ数を覚えておくための配列を準備します。
9〜10行目
0番目と1番目のフィボナッチ数は決まっているのであらかじめ代入します。
20行目
n番目のフィボナッチ数がまだ計算されていなかったときだけ再帰呼び出しでフィボナッチ数を計算します。
それではWebブラウザでプログラムを実行してみてください。25や30では計算時間は一瞬です。300でも全く問題なく計算できます。3000だとスタックオーバーフローになります。
このようにちょっとしたアルゴリズムの違いでパフォーマンスには大きな差が生まれます。
再帰を使わないでフィボナッチ数を計算する
フィボナッチ数の計算も再帰を使わないで記述することができます。どのようにしたらよいでしょうか。
この場合、数式の定義は忘れて最初の説明どおりに素直に実装するとよいでしょう。つまり0から始まって1ずつ増えるようにループしてn番目まで計算すればよいのです。プログラムは以下になります。
<html>
<body>
<script type="text/javascript">
function startCalc() {
document.getElementById("disp").innerHTML = "";
var number = document.getElementById("number").value;
display("disp", number + "のフィボナッチ数=" + fibonacci(number));
}
function fibonacci(n) {
fibonacciResult = new Array();
fibonacciResult[0] = 0;
fibonacciResult[1] = 1;
for (i = 2; i <= n; i++) {
fibonacciResult[i] =
fibonacciResult[i - 1]
+ fibonacciResult[i - 2];
}
return fibonacciResult[n];
}
function display(id, str) {
var element = document.getElementById(id);
element.innerHTML += str + "<br/>";
}
</script>
<input type="text" id="number">
番目のフィボナッチ数を計算する
<input type="submit" value="計算開始" onclick="startCalc()">
<div id="disp"></div>
</body>
</html>
フィボナッチ数列の場合は再帰を使わなくても分かりやすいですし、パフォーマンスも改善版とほぼ同等です。こういった場合はどちらで実装しても問題ないということになります。
Copyright © ITmedia, Inc. All Rights Reserved.