再帰でハノイの塔を攻略せよ：コーディングに役立つ！アルゴリズムの基本（3）（1/3 ページ）

プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか（編集部）

[山下寛人，オイシックス株式会社] PC用表示関連情報

LINE

Hatena

最大公約数を求める

　「最大公約数を求めるプログラムを作って」といわれて、すぐに書けるでしょうか。

　一般的には小学校で最大公約数の求め方を教わります。2つの数を共通する素数で割っていくというものです。そのままプログラムしようとすると、まず素数を求めるところから始めなければならず、少々難しそうです。

　最も単純にやるとすれば、2つの数の小さいほうから1ずつ減らして両方の数を割っていき、どちらも余りが0になるものを求めるという方法でよいでしょう。しかしこのやり方は無駄が多そうです。

　「ユークリッドの互除法」という方法を使うと簡単にプログラムにすることができます。ユークリッドの互除法とは以下のような方法で最大公約数を求めるやり方です。

2つの整数a、bがある
aをbで割った余りをrとする
aとbの最大公約数はrとbの最大公約数になる
次にbをrで割った余りを求める
これを繰り返して余りが0になったときの除数が最大公約数

　このやり方なら非常に簡単にプログラムにすることができます。

<html>
<body>
<script type="text/javascript">
  function saidaikouyakusuu(a, b) {
    display("saidaikouyakusuu", "計算中：" + a + "と" + b + "の最大公約数"); 
    var r = a % b;
    if (r == 0) {
      return b;
    }
    return saidaikouyakusuu(b, r);
  }
  function display(id, str) {
    var element = document.getElementById(id);
    element.innerHTML += str + "<br/>";
  }
</script>
 
<div id="saidaikouyakusuu"></div>
 
<script type="text/javascript">
  display("saidaikouyakusuu", "最大公約数は" + saidaikouyakusuu(14, 21));
</script> 
 
</body> 
</html>

　21行目のdisplay関数でプログラムの実行が始まります。

　4～11行目のsaidaikouyakusuu関数が最大公約数を求める関数です。非常に短いプログラムです。

　この関数の最後の部分でsaidaikouyakusuu関数を呼び出しています。このように関数の中で自分自身を呼び出すようなやり方を「再帰」といいます。さまざまなアルゴリズムで再帰をよく使いますので、今回は再帰を使ったアルゴリズムを紹介して理解を深めます。

青い部分を赤くする

　HTMLのすべてのタグを調べて、背景色が青くなっているタグの背景色を赤に変えるプログラムを作ってみましょう。

　タグの名前やidが限定されていればdocument.getElementByTagName()やdocument.getElementById()を使うことができます。しかし、この場合はすべてのタグを調べないといけないので適用できません。

　ループして調べていくとすると、タグの入れ子が問題になります。あるタグの子ノードのリストはchildNodesとして取得できます。このリストに対してループしてそれぞれの要素を調べればよいのですが、さらに子ノードがある場合があります。子ノードの入れ子が何重か最初から分かっていればそれだけループを入れ子にすればよいのですが、何重なのかは分かりません。

　こういう場合は再帰を使うと簡単に実装できます。

<html>
<script type="text/javascript">
  function changeColor(element) {
    if (element == null) {
      var element = document.body;
    }
    if (element.childNodes.length > 0) {
      changeColor(element.firstChild);
    }
    if (element.nodeType == 1) {
      if (element.style.backgroundColor == "blue") { 
        element.style.backgroundColor = "red";
      }
    }
    if (element.nextSibling != null) {
      changeColor(element.nextSibling);
    }
  }
</script>
<body>
 
<form>
<table border="1">
  <tr>
    <td style="background-color: blue;">赤くしたい</td>
    <td>赤くしない</td>
  </tr> 
  <tr>
    <td><span style="background-color: blue;">赤くなれ</span></td>
  </tr>
</table>
<div style="width: 200px; border-style: solid;">
<span>ここは赤くしない</span>
</div>
<div id="test1"><span id="test2">タグを入れ子にする</span></div>
</form>
<input type="button" value="実行開始" onclick="changeColor()" />
 
</body>
</html>

　まずは、Webブラウザで実行してみてください。「実行開始」と書いてあるボタンをクリックすると、画面で青くなっている部分が赤く変わります。

　プログラムを解説します。大きな流れとしては以下のようになります。

子ノードがあるか調べる
子ノードがあれば下の階層に移動する
子ノードがなくなるまで一番下まで下る
子ノードがなければそのノードの背景色をチェックして青だったら赤に変える
同じ階層に次のノードがあれば次のノードに移動する
同じ階層に次のノードがなければ上の階層に戻って処理を続ける

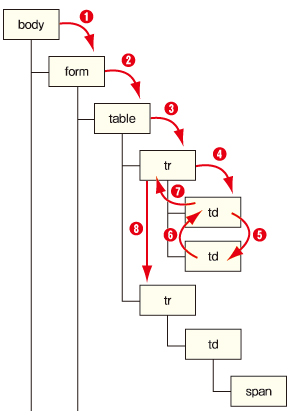
　タグのチェック順を図にすると次のようになります。

子ノードがあるので下の階層に移動する
子ノードがあるので下の階層に移動する
子ノードがあるので下の階層に移動する
子ノードがあるので下の階層に移動する
子ノードがないので背景色をチェックする。次のノードに移る
子ノードがないので背景色をチェックする。次のノードがないので呼び出し元に戻る
呼び出し元に戻る
背景色をチェックする。次のノードがあるので次のノードに移動する

　あとは同じ要領で処理が続きます。なかなか難しい処理ですが非常にスマートに実装することができました。

再帰を使わないで実装する

　再帰を使わないで同じ処理を実装してみましょう。プログラムは以下のようになります。

<html>
<script type="text/javascript">
  function changeColor() {
    var current = document.body;
    var stack = new Array();
    var isPopped = false;
    while (current != null) {
      if (!isPopped) {
        if (current.childNodes.length > 0) {
          stack.push(current);
          current = current.firstChild;
          continue;
        }
      }
      if (current.nodeType == 1) {
        if (current.style.backgroundColor == "blue") {
          current.style.backgroundColor = "red";
        }
      }
      isPopped = false;
      current = current.nextSibling;
      if (current == null) {
        current = stack.pop();
        isPopped = true;
      }
    }
  }
</script>
<body>
 
<form>
<table border="1">
  <tr>
    <td style="background-color: blue;">赤くしたい</td>
    <td>赤くしない</td>
  </tr>
  <tr>
    <td><span style="background-color: blue;">赤くなれ</span></td>
  </tr>
</table>
<div style="width: 200px; border-style: solid;">
<span>ここは赤くしない</span>
</div>
<div id="test1"><span id="test2">タグを入れ子にする</span></div>
</form>
<input type="button" value="実行開始" onclick="changeColor()" />
 
</body>
</html>

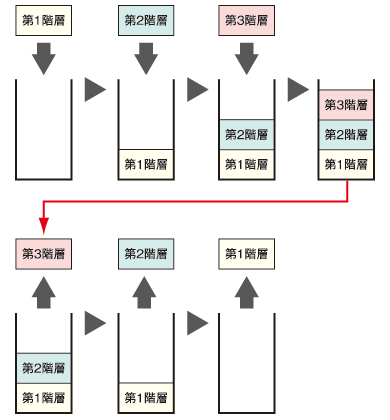
　大まかな処理の流れは再帰を使った場合と同様です。子ノードがないところまで階層を下ってゆき、同じ階層のノードを順にチェックしていきます。一番下の階層を全部調べ終わった後、上の階層に戻らないといけません。再帰の場合は特に意識しなくてすみましたが、どこに戻るのかを覚えておくためにスタックを使います（スタックの詳細については前回の解説を参照してください）。

　子ノードがあるとき、下の階層に移動する際に、後で戻れるよう、スタックに保存します。スタックは後入れ先出しなので、上の階層から下に移動していくと、戻るときは下から上に戻ることができます。

　popした後、その要素の子ノードがあるか調べると、必ず存在するので無限ループになってしまいます。子ノードがある場合にその要素をpushしているためです。この無限ループを避けるためisPoppedという変数を使い、popしたものについては子ノードがあるか調べる処理をしないで次のノードに移るようにします。

　このように再帰を使ったプログラムは再帰を使わないプログラムに書き換えることができます。書き換える際にはスタックを活用することがよくあります。ただし、この例を見ても分かるように、再帰を使ったほうがスマートに分かりやすく記述できる場合が多いです。

フィボナッチ数列のn番目を求める

　　　　　　 | 次のページへ

再帰でハノイの塔を攻略せよ：コーディングに役立つ！ アルゴリズムの基本（3）（1/3 ページ）

最大公約数を求める

青い部分を赤くする

再帰を使わないで実装する

Coding Edge 記事ランキング

再帰でハノイの塔を攻略せよ：コーディングに役立つ！アルゴリズムの基本（3）（1/3 ページ）