データ量を操る圧縮／展開を究めよう：コーディングに役立つ！ アルゴリズムの基本（8）（2/5 ページ）

プログラマたるものアルゴリズムとデータ構造は知っていて当然の知識です。しかし、教科書的な知識しか知らなくて、実践的なプログラミングに役立てることができるでしょうか（編集部）

[山下寛人，オイシックス株式会社]

ランレングス法が苦手なデータに変えてみる

　ランレングス法は、データが連続している場合には有効ですが、連続していないデータの場合は、1文字が、文字と文字数「1」という2つのデータになってしまい、逆にデータ量が増えてしまいます。

　先のプログラムの12行目から20行目を以下の文章に差し替えてみてください。文章は英語版Wikipediaから引用しました。

Some writers restrict the definition of algorithm to procedures that eventually finish. In such a category Kleene places the "decision procedure or decision method or algorithm for the question" (Kleene 1952:136). Others, including Kleene, include procedures that could run forever without stopping; such a procedure has been called a "computational method" (Knuth 1997:5) or "calculation procedure or algorithm" (Kleene 1952:137); however, Kleene notes that such a method must eventually exhibit "some object" (Kleene 1952:137). Minsky makes the pertinent observation, in regards to determining whether an algorithm will eventually terminate (from a particular starting state):

But if the length of the process is not known in advance, then "trying" it may not be decisive, because if the process does go on forever ? then at no time will we ever be sure of the answer (Minsky 1967:105). As it happens, no other method can do any better, as was shown by Alan Turing with his celebrated result on the undecidability of the so-called halting problem. There is no algorithmic procedure for determining of arbitrary algorithms whether or not they terminate from given starting states. The analysis of algorithms for their likelihood of termination is called termination analysis. See the examples of (im-)"proper" subtraction at partial function for more about what can happen when an algorithm fails for certain of its input numbers ? e.g., (i) non-termination, (ii) production of "junk" (output in the wrong format to be considered a number) or no number(s) at all (halt ends the computation with no output), (iii) wrong number(s), or (iv) a combination of these. Kleene proposed that the production of "junk" or failure to produce a number is solved by having the algorithm detect these instances and produce e.g., an error message (he suggested "0"), or preferably, force the algorithm into an endless loop (Kleene 1952:322). Davis does this to his subtraction algorithm ? he fixes his algorithm in a second example so that it is proper subtraction (Davis 1958:12-15). Along with the logical outcomes "true" and "false" Kleene also proposes the use of a third logical symbol "u" ? undecided (Kleene 1952:326) ? thus an algorithm will always produce something when confronted with a "proposition". The problem of wrong answers must be solved with an independent "proof" of the algorithm e.g., using induction: We normally require auxiliary evidence for this (that the algorithm correctly defines a mu recursive function), e.g., in the form of an inductive proof that, for each argument value, the computation terminates with a unique value (Minsky 1967:186).

　これをランレングス法で圧縮します。なんと、データ量はおよそ倍になってしまいました。

2進数のおさらい

　先ほどのデータを圧縮するためにハフマン符号というアルゴリズムを紹介します。その前にビットデータを取り扱うため、2進数とビット演算についておさらいしたいと思います。

　通常、私たちが使っている数は、10になるとけたが増えます。100（10の2乗）になると2けた増え、1000（10の3乗）になると3けた増えます。これを10進数といいます。

　2になるとけたが増えるのが2進数です。0、1までは10進数と同じですが、「2」は2進数では「10」になります。「3」は「11」。「4」になると「100」となります。

　2進数になると数値がすべて0と1で表現できます。コンピュータは内部では電気信号が「ある」「ない」の2通りでデータを管理しています。そのためコンピュータの内部では、通常、2進数でデータを取り扱います。

　2進数は英語ではbinary numberと呼びます。バイナリという言葉もよく使われます。

ビットとバイトのおさらい

　コンピュータのデータ量を表す単位として、ビットとバイトがあります。

　1ビットは、先ほどの2進数の1けた、つまり0か1のどちらかだけのデータ量です。

　1バイトは、2進数8けたのデータ量、つまり8ビットのデータ量です。8ビットの最小の数値は0、最大は2進数で11111111＝10進数で255になります。従って、1バイトでは0から255までの範囲の数値を保持できます。

　あるデータを2進数として考えて、1けたずらすことをビットシフトと呼びます。例えば、「1011」という2進数を左に1けたシフトすると「10110」、右に1けたシフトすると「101」になります。

　同じ要領で10進数を考えてみます。例えば、「123」を左に1けたシフトすると「1230」となり10倍になっています。右に1けたシフトすると「12」となり1/10になっています（小数点以下は無視しています）。

　同様に2進数は左にシフトすると2倍、右にシフトすると1/2になります。

　なお、ビットシフトにも種類あって、上のように0を入れるビットシフトは論理シフトといいます。

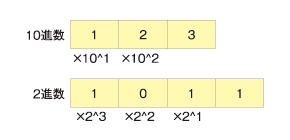
　2進数を10進数に変換する方法を考えてみましょう。先に10進数を考えると分かりやすいでしょう。例えば、「123」だと1×10^2＋2×10^1＋3という構成になっています。

　同様に2進数では右から1けた目は1か0、2けた目は2^1、3けた目は2^2……という具合になっています。それぞれのけたに、このけたごとの数値を掛けて足せばよいのです。

　例えば「1011」だったら、 1*2^3+0*2^2+1*2^1+1=11となります。

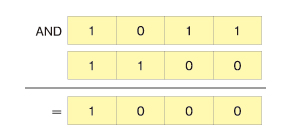
　ビット演算の中にはAND演算というものあります。2つの数を2進数で表現します。そして、それぞれのけたを合わせて並べます。それぞれのけたごとに、両方の値が「1」なら「1」、そうでなければ「0」とします。最終的にできた結果がAND演算の結果です。