計算高速化のための強力な武器、NumPyのブロードキャスティングとSciPyの疎行列処理:Pythonで始める機械学習入門(4)(2/2 ページ)
最近流行の機械学習/Deep Learningを試してみたいという人のために、Pythonを使った機械学習について主要なライブラリ/ツールの使い方を中心に解説する連載。今回は、うまく使うと計算時間を短縮できるNumPyのブロードキャスティングと、機械学習で利用価値の高いSciPyにおける疎行列の扱い方を取り上げる。
SciPyにおける疎行列の扱い方
ここからは、SciPyにおける疎行列の扱い方を見ていきます。
疎行列とは
疎行列とは、ほとんどの要素がゼロであるような行列で、ゼロ以外の要素のみを保存して計算することで、メモリや計算速度を節約できる仕組みです。疎行列ではない、よくある行列を「密行列」と呼ぶこともあります。
疎行列は、機械学習における多くの分野で有用です。特に疎行列が有効な例としては、DVDレンタルサイトのレコメンデーション(自動推薦)システムが考えられます。入力としては、ユーザーが映画に付けた評価値(レーティング)を1〜5の5段階で与えられているものとします。
例えば、「ユーザーU1が映画M1を2と評価しM2を5と評価した。ユーザーU2がM2を2と評価しM3を1と評価した……」などというデータ(下表参照)が与えられたとします。DVDレンタルサイトでは、多くのユーザーとコンテンツを持っており、1人のユーザーが見たコンテンツはごく一部ですが、この評価値のデータは、ユーザー数×コンテンツ数の行列になり巨大な行列になります。しかし、ほとんどの要素が欠損値になり、欠損値を0で表すとすると疎行列を使えば効率的に表現できます。
| ユーザー\映画 | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| U1 | 2 | 5 | |||
| U2 | 2 | 1 | |||
| U3 | 3 | 1 | 2 |
SciPyには、疎行列を表すクラスが多数ありますが、ここでは、その中でも特に機械学習で利用価値の高いlil_matrix、csr_matrix、csc_matrixについてのみ説明することにします。
lil_matrixクラス
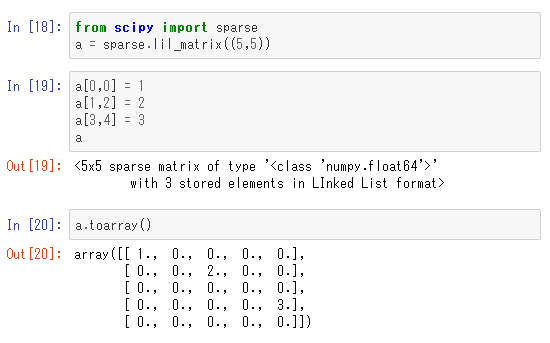
下記コードのようにtoarrayメソッドを呼ぶと、疎行列を密行列に変換してくれるので、実験的なコードで動作を確認するには便利です。しかし通常、疎行列型を使いたくなるようなケースというのは「行列のサイズが巨大になる」場合なので、実データでtoarrayメソッドを使うことはあまりないでしょう。
ここまでで、lil_matrixを使いましたが、「最初にデータを格納する」にはlil_matrix型を使うのが便利です。例えば、「a[i,j]=v」の形で「i,j」成分に値を設定できます。
一方で、このlil_matrixは、「行列の計算を行う」には効率が良くないため、計算効率が良いcsr_matrixやcsc_matrixに変換してから使うのが普通です。
lil_matrixをtocsrメソッドでcsr_matrixとして計算
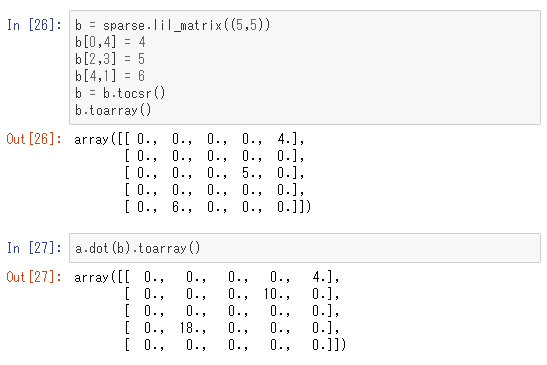
この例では、サイズが小さいのであまり計算速度は気にならないのですが、tocsrメソッドを使ってaをcsr_matrix型に変換してみます。
疎行列について行列積を計算するには、dotメソッドを利用します。まずは、疎行列と密行列の積を計算してみます。
もちろん、疎行列同士の積も計算できます。
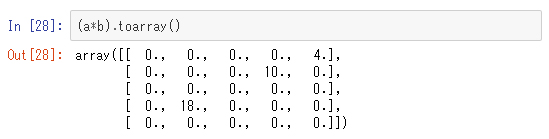
疎行列型の場合は普通の配列とは異なり、乗算演算子(*)でも行列の積を計算できます。
csr_matrixとcsc_matrixの違い
以上、csr_matrix型を使って計算しましたが、代わりにcsc_matrixを使ったとしても、速度を含めて全く同じように計算ができます。では、csr_matrixとcsc_matrixの違いは何かというと、データの格納形式です。
csr_matrixでは非ゼロ要素のデータが行方向に格納されていて、csc_matrixでは列方向に格納されています。これは、指定した行(列)を取り出す手続きが必要なときに影響します。csr_matrixでは指定した行を取り出すのが高速で、csc_matrixでは指定した列を取り出すのが高速です。
指定した行、列を取り出すgetrowメソッド、getcolメソッド
指定した行、列を取り出すには、それぞれgetrowメソッド、getcolメソッドを使います。
疎行列型のdotメソッド
疎行列ではなくて疎ベクトル(要素のほとんどが0であるベクトル)を使いたくなることがあるかもしれませんが、疎ベクトルを表す明示的な型はないので、行数または列数が1の疎行列で代用します。
このように、疎行列型(csr_matrix、csc_matrix)のdotメソッドは、密行列/疎行列(ベクトル)を引数にすることができ、そのデータ型に応じた最適なアルゴリズムで計算されます。
NumPyのdotの引数として、疎行列の場合は想定されていない
一方で、密行列×疎行列のように、左側に密行列が来るケースは注意が必要です。前回、numpy.dotを使った密行列同士の積を説明しましたが、これは引数が疎行列の場合はうまくいきません。
また、NumPyのarray型にもdotメソッドというのがありますが、その引数が疎行列のときもうまくいきません。
これは、NumPyのdotの引数として、疎行列の場合は想定されていないからです。こういう場合は乗算演算子を使います。
注意!「乗算演算子の内部動作について」
乗算演算子によるこのような掛け算は、疎行列型の(この場合は、変数aの)「__rmul__」というスペシャルメソッドによって定義されています。
一般的には、クラス定義内で__rmul__メソッドを定義することで、そのクラスに対する左からの掛け算(つまり他のオブジェクトに対する、そのクラスの右からの掛け算)を定義できます。
乗算演算子を使わずにdotメソッドを使って同等なことをやろうとすると「vA=(ATvT)T」という同値変形を用いて以下のようになります。
ここで、Tは転置行列を意味するプロパティで、vについては特に縦横を区別する必要がない(つまり転置する必要がない)のは前述の通りです。
疎行列を扱う際の注意点
まとめると、疎行列の扱い方については、以下のようなことに気を付ける必要があります。
- データの格納はlil_matrixが使いやすい。しかし計算にはcsr_matrixまたはcsc_matrixに変換してから使う方がよい
- 指定した行を取り出す作業が必要なときはcsr_matrixを、指定した列を取り出す作業が必要なときはcsc_matrixを使う
- 疎行列の積には疎行列型のdotメソッドまたは乗算演算子(*)を使う。特に疎行列の左から密行列を掛ける場合は気を付ける
次回は、Matplotlibを使ったグラフの描画やデータの可視化
今回はNumPyの配列によるブロードキャスティングとSciPyの疎行列について説明しました。両方ともうまく使いこなすと計算高速化のための強力な武器になりますが、それらを駆使したコードは数学的同値変形に慣れていない人にはトリッキーに見えるかもしれません。
次回は、連載第1回で紹介したMatplotlibを使ったグラフの描画やデータの可視化について解説する予定です。お楽しみに。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 機械学習、ビッグデータ解析に欠かせない、PythonをWindowsにダウンロードしてインストール、アンインストールする
機械学習、ビッグデータ解析に欠かせない、PythonをWindowsにダウンロードしてインストール、アンインストールする
本連載では、さまざまなソフトウェアのインストール、実行するためのセットアップ設定、実行確認、アンインストールの手順を解説する。今回は、Pythonとは何か、Pythonのインストールとアンインストールについて解説。Pythonがよく使われる機械学習やビッグデータ解析を始める参考にしてほしい。 ITエンジニアがデータサイエンティストを目指すには?
ITエンジニアがデータサイエンティストを目指すには?
それぞれの専門分野を生かした「データサイエンスチーム」を結成すればデータ活用への道は短縮できる。そのとき、ITエンジニアはどんな知識があればいい? データサイエンティストとして活動する筆者が必須スキル「だけ」に絞って伝授します。 Recurrent Neural Networkとは何か、他のニューラルネットワークと何が違うのか
Recurrent Neural Networkとは何か、他のニューラルネットワークと何が違うのか
本連載では、Deep Learningの中でも、時系列データを扱うRecurrent Neural Networkについて解説。加えて、その応用方法として原稿校正(誤字脱字の検知)の自動化について解説します。