第3回 ディープラーニング最速入門 ― 仕組み理解×初実装（後編）：TensorFlow 2＋Keras（tf.keras）入門（2/3 ページ）
いよいよ、ディープラーニングの学習部分を解説。ニューラルネットワーク（NN）はどうやって学習するのか、Pythonとライブラリではどのように実装すればよいのか、をできるだけ簡潔に説明する。
（6）学習：トレーニング
それでは、いよいよ学習を行っていこう。
Playgroundによる図解
Playgroundを開いて、上部にある（6）の［実行／停止］ボタンをクリックするだけで、学習が始まる（図6-1）。
バックプロパゲーション（誤差逆伝播法）
学習（＝最適化）は、出力層から隠れ層へと、ニューラルネットワークの各層を逆順に進みながら、徐々に各ニューロンにおける各接続線の重みやバイアスを更新していく。前回説明したフォワードプロパゲーション（順伝播）とは逆の流れである。逆に伝播していくことから、バックプロパゲーション（Back-propagation：Backprop、Backward propagation、逆伝播、誤差逆伝播法）と呼ばれる。
バックプロパゲーションは、ニューラルネットワークの核となる機能なので、本来であれば、数式を理解し、実際にフルスクラッチでコードを書いて経験してみるのが一番である。しかしこれには、前述の偏微分と線形代数の理解が欠かせない。バックプロパゲーションのフルスクラッチ実装については、今後の連載企画に委ねるとして、今回は上記の機能概要紹介にとどめる。
エポック単位でのステップ学習
ニューラルネットワークでの学習単位はエポックと呼ばれる。1エポックで全ての訓練データを1回学習したことになる。
Playgroundで実行すると、永遠に学習してしまうため、エポックのメーターが回り続けることになる。しかし、1エポックの学習ごとにどのような変化があるかを見たいときもあるだろう。そのようなときは、学習を停止させてから［実行／停止］ボタンの右にある［ステップ］ボタンをクリックすればよい（図6-2）。
Pythonコードでの実装例
それでは、学習をコードで実装してみよう。そのコードを書く前に、前々回の復習として、データを取得して、訓練用／精度検証用にデータ分割するコードを再掲しておこう。
# （必要に応じて）座標点データを生成するライブラリをインストールする必要がある
#!pip install playground-data
# playground-dataライブラリのplygdataパッケージを「pg」という別名でインポート
import plygdata as pg
# 問題種別で「分類（Classification）」を選択し、
# データ種別で「2つのガウシアンデータ（TwoGaussData）」を選択する場合の、
# 設定値を定数として定義
PROBLEM_DATA_TYPE = pg.DatasetType.ClassifyTwoGaussData
# 各種設定を定数として定義
TRAINING_DATA_RATIO = 0.5 # データの何％を訓練【Training】用に？ (残りは精度検証【Validation】用) ： 50％
DATA_NOISE = 0.0 # ノイズ： 0％
# 定義済みの定数を引数に指定して、データを生成する
data_list = pg.generate_data(PROBLEM_DATA_TYPE, DATA_NOISE)
# データを「訓練用」と「精度検証用」を指定の比率で分割し、さらにそれぞれを「データ（X）」と「教師ラベル（y）」に分ける
X_train, y_train, X_valid, y_valid = pg.split_data(data_list, training_size=TRAINING_DATA_RATIO)
学習を行うコードは、リスト6-2のようになる。
# 定数（学習方法設計時に必要となるもの）
BATCH_SIZE = 1 # バッチサイズ： 1（選択肢は「1」〜「30」）
EPOCHS = 100 # エポック数： 100
# 学習する（※まだ実行しないこと）
hist = model.fit(x=X_train, # 訓練用データ
y=y_train, # 訓練用ラベル
validation_data=(X_valid, y_valid), # 精度検証用
batch_size=BATCH_SIZE, # バッチサイズ
epochs=EPOCHS, # エポック数
verbose=1) # 実行状況表示
最初に、バッチサイズとエポック数が定数として定義されている。バッチサイズはこの後で説明するが、Playgroundと同様に取りあえず1を指定する。エポック数は100が指定されているので、100エポックの学習を行うことになる。
実際の学習は、modelオブジェクトのfitメソッドで行える。このメソッドは、
fit(
x=None,
y=None,
validation_data=None,
batch_size=None,
epochs=1,
verbose=1
)
と定義されており（※不要な引数は説明を割愛）、各引数の意味は以下の通りである。
- 第1引数のx： 訓練用データを指定する。今回は、先ほど作成したX_train（＝訓練データの座標点）を指定
- 第2引数のy： 訓練用ラベルを指定する。今回は、先ほど作成したy_train（＝訓練データの教師ラベル）を指定
- 第3引数のvalidation_data： 精度検証データとそのラベルをタプルで指定する。今回は、先ほど作成したX_validとy_validをタプルで指定
- 第4引数のbatch_size： バッチサイズを指定する。今回は、定数として定義したBATCH_SIZEを指定
- 第5引数のepochs： エポック数を指定する。今回は、定数として定義したEPOCHSを指定
- 第6引数のverbose： 進行状況や結果のログを標準出力する。1を指定するとプログレスバー付きで表示され、2を指定するとエポックごとにより詳しく表示される。0を指定すると出力されない。今回は1を指定する
また、fitメソッドはHistoryオブジェクト（この例ではhist）を戻り値として返す。Historyオブジェクトのhistory属性には、トレーニング（学習）時の各エポックでの損失値や評価関数値が記録されており、さらに上記のように精度検証データも指定された場合はその損失値や評価関数値も記録されている。この記録の見方は、後述の「評価」で説明する。
以上で学習のコードも完了だ。ここで実行すると、学習が実際に行われるのだが、まだ実行しないでほしい（※実行すると、その結果が保存されてしまう。この状態で、次の「リスト6-3 ミニバッチ学習」を実行すると、学習済みモデルに追加で学習することになってしまうため）。次に、損失や正解率を見ていくが、その前に、説明をスキップしていたバッチサイズについて言及しておこう。
（6）学習： バッチサイズ
Playgroundによる図解
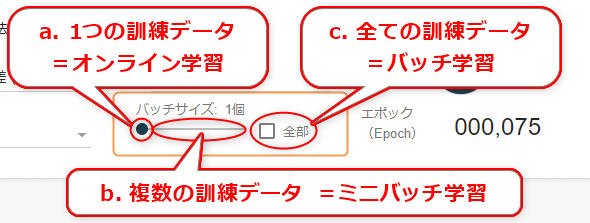
あらためて示すと、バッチサイズは図6-3のように設定できる。
前述の「勾配法」の節でも簡単に示したが、バッチサイズ（Batch size）とは、「どのくらいの数量（＝サイズ）の訓練データをまとめて学習するか」を示す数値で、
a. 1つの訓練データ： オンライン学習（Online training ）
b. 複数の訓練データ： ミニバッチ学習（Mini-batch training ）
c. 全ての訓練データ： バッチ学習（Batch training ）
という3パターンに大別できる。オンラインとは、文字通り、連続的につながっているデータを1つずつ処理して重みとバイアスを更新していくことを意味する。バッチとは、文字通り、一群の全データをまとめて処理して一気に重みとバイアスを更新していくこと。そしてミニバッチとは、その中間で、ある程度の小さいまとまりごとに処理して、その単位で重みとバイアスを更新していくことを意味する。
それぞれの代表的な勾配法にも以下のような違いがある。
a. オンライン学習＝確率的勾配降下法（SGD：Stochastic Gradient Descent）
b. ミニバッチ学習＝ミニバッチ勾配降下法（Mini-batch Gradient Descent、上記と同じくSGDとも呼ぶ）
c. バッチ学習＝最急降下法（Steepest Descent、バッチ勾配降下法：Batch Gradient Descent）
勾配法の名前を見ると、aとbはSGD（Stochastic Gradient Descent）で同じものと見ることができる。一方、cは「勾配降下法」（GD：Gradient Descent）とも呼ばれるが、「Stochastic」（確率的）が付いていない。「確率的」とは、データをランダムサンプリング（ランダムに抽出）して、勾配を計算して重みとバイアスを更新することを指す。本来であれば、全データを使って厳密に学習してから、重みとバイアスを更新するのが妥当だと考えられるだろう。しかし、確率論に基づけば、そのような部分的なデータを使っても、重みとバイアスを更新していけるというわけだ。
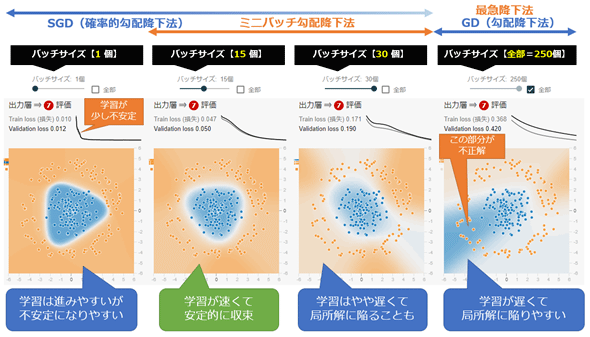
参考までに、［バッチサイズ］に1個／15個／30個／全部（＝250個）を指定した場合の学習結果の違いを、図6-4にまとめた。
学習率に応じて最適なバッチサイズも変わるため一概には言えないが、学習率0.03という状況下における、図6-4に示す各バッチサイズによる影響／効果を以下にまとめた。バッチサイズを決める上で参考にしてほしい。
まず、左端の1個では、全て個別に（この例ではデータ1個×250イテレーション）学習していくので、1エポックが完了するスピードはやや遅いが、学習は進みやすい。実際、この例では100エポックで損失（loss）は0.01となっており、ほぼ学習が終わっている。その半面、損失の下降線を描いているグラフを見ると一部がジグザグと震えているのが分かるが、このように、1つのデータに学習が揺さぶられて不安定になりやすい欠点もある。
次の15個は、1エポック（この例ではデータ15個×16イテレーション）の学習スピードが速く、しかも一直線に安定的に学習できている。この中では最良である。
1つ飛ばして右端の全部（＝250個）は、全データを使うので今度は計算量が多くなって、1エポック（この例ではデータ250個×1イテレーション）が完了するスピードは遅くなり、しかも学習もなかなか進まない。バッチ学習（最急降下法）は、局所解に陥りやすいという欠点もあるので、多くのケースでSGDの方が好ましい。実際に、図6-4をこのまま学習を続けても、左下にあるオレンジ色の丸い点の背景色は青色（＝不正解）のままになり、損失が減らなくなった。これは局所解に陥っている状態である。
それを踏まえて、1つ前の30個を見ると、局所解を何とか避けられており、このまま学習を続けると損失は0に近づく。何度か実行を試すと局所解に陥ることもあったので、バッチサイズが大きすぎる場合には局所解への注意が必要だ。1エポック（この例ではデータ30個×8イテレーション）が完了するスピードは、データが小分けになって計算量が減るのでバッチ学習よりも速いが、バッチサイズ15個よりは計算量が比較的多いのでやや遅い。
Pythonコードでの実装例
バッチサイズの設定方法は前述のリスト6-2で説明済みである。具体的にはリスト6-3のように、定数BATCH_SIZEに「15個」を指定するだけだ。もし全データ（最急降下法）を使いたい場合は、「None」を指定すればよい。
# 定数（学習方法設計時に必要となるもの）
BATCH_SIZE = 15 # バッチサイズ： 15（選択肢は「1」〜「30」）
EPOCHS = 100 # エポック数： 100
# 学習する
hist = model.fit(x=X_train, # 訓練用データ
y=y_train, # 訓練用ラベル
validation_data=(X_valid, y_valid), # 精度検証用
batch_size=BATCH_SIZE, # バッチサイズ
epochs=EPOCHS, # エポック数
verbose=1) # 実行状況表示
以上で学習の説明は終わりである。ここで実際にリスト6-3のコードを実行してみよう。次に、その学習の結果について見ていこう。
（7）評価： 損失のグラフ
Copyright© Digital Advantage Corp. All Rights Reserved.