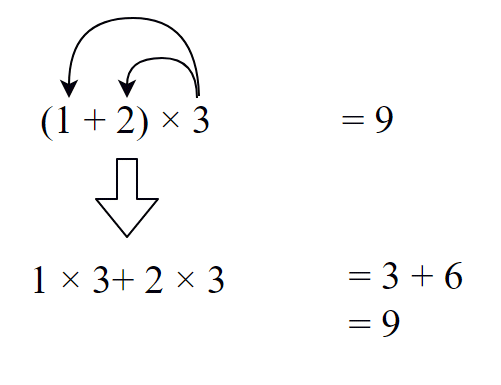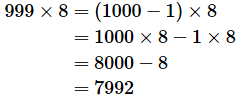連載

2020年3月2日

AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ！：AI・機械学習の数学入門（1/4 ページ）

機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算（足し算／引き算／掛け算／割り算）」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学／高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。

[羽山博，著] PC用表示関連情報

LINE

Hatena

連載目次

機械学習は、人間の日常とそう変わらない

　この連載を読もうとする方々は機械学習について興味をお持ちなので、回帰とか分類といった用語は既にどこかで見聞きしていることと思います。また、機械学習がどういうものかというイメージもそれぞれお持ちだと思います。しかし、多くの人が、機械学習を必要以上に難しく捉えすぎなのではないか、と最近つくづく感じています（私自身、そうでした）。そこで、もう少し身の丈に引き寄せて、機械学習を捉え直してみることにします。

　実際のところ、機械＝コンピューターがやっていることは、人間のやっていることとよく似ていて、意外に単純です（むしろ人間がやっていることの方がはるかに複雑です）。簡単な例で見てみましょう。皆さんは「数当てゲーム」をやったことがあると思います。あまりにも単純すぎて、オトナになってからはやらないかもしれませんが、プログラミングの練習問題としてやらされたことのある人もいるでしょう。

　試しにやってみましょう。今、私が考えている数字を当てて下さい。数字は0～99のどれかです。……といっても、読者の皆さんと私は直接対話しているわけではないので、皆さんの代表として誰か（Aさんとします）に答えてもらうことにします。

Aさん　それじゃ、50から
私　まあ、そうきますよね。もっと下です
Aさん　じゃあ25
私　もうちょっと上です
Aさん　37ぐらい？
私　今度はもうちょっと下です
Aさん　31
私　もうちょっと下
Aさん　28
私　近い。もうちょっとだけ上
Aさん　29
私　正解です！

　ここでAさんがやっていることは、機械学習ととてもよく似ています。Aさんは適当な初期値を決め、私からのヒントを基に値を調節していきます。そして、最適な解を見いだす、というわけです*1。ちなみに、Aさんは無意識のうちに「候補を半分ずつに絞っていく」という方法を採っています。これは（名前を覚える必要はないですが）二分法と呼ばれるアルゴリズムで、数字が100個であれば7回までの挑戦で確実に数字が当てられます（なぜ7回なのかは、対数を使えば簡単に計算できますが、それは回を改めて説明します）。

*1　プログラミングの練習問題として作る数当てゲームでは、人間が数値を予測します（これは上記の「Aさん」の役割です）。コンピューターは、「その予測値が正解よりもどれくらい上か下か」というヒントを人間に提示します（これは上記の「私」の役割です）。そして、人間が正解に向けて数値を調整していきます。

　この「数当てゲーム」の流れは、各役割を担う担当者が違うというだけで、機械学習でも同じです。

　機械学習では、コンピューターが数値を予測します（＝「Aさん」の役割）。「その予測値が正解よりもどれくらい上か下か」というヒントは、（基本的に人間が作成した）正解情報から自動的に計算され、コンピューターに提示されます（＝「私」の役割）。そして、コンピューターが正解に向けて数値を調整していきます。

　いや、そんなのは機械学習じゃないぞ、と言われる向きもあるかと思います。確かに二分法は単純なアルゴリズムなので、「機械学習」から見るとミジンコのようなものかもしれません（リアルなミジンコはとても複雑ですが）。しかし、出発点としてはこういうイメージで十分かと思います。つまり、何らかの方法に従って少しずつ値を変えていき、最適な解を得るということですね。機械学習なんて数当てゲームの延長にすぎない……と考えれば、少しは身近に感じられるのではないでしょうか。学びを深めていけば、機械学習がどういうものであるかというイメージも少しずつ更新していけるでしょう。

　機械学習の種類として登場する回帰や分類といった用語についても、上のような例から「実はカンタンなことなんだよ」というお話をしてもいいのですが、ダラダラと前置きを話していても退屈なだけなので、そろそろ本題に入っていくこととしましょう（必要に応じて、その都度、説明します。また、皆さんなりに、日常のこういうことと同じだよね、という例を探してもらうのもいいでしょう）。

機械学習で使われる数学は結局のところ四則演算だけ！

　ところで、この連載のテーマは機械学習そのものではなく、「機械学習で使われる数学」です。これについても線形代数とか微分法とかが使われる、といった話はご存じでしょう。しかし、それらの用語を聞くだけで「難しい数学はちょっと……」と腰が引けてしまう人も多いようです。そこで諦めてしまうのはとても残念なので、この連載では、多くの人が理解できる中学／高校の数学レベルから機械学習に必要最小限の部分だけをおさらいして、難しそうな数式が書かれた機械学習の本を抵抗なく読めるようにしようというわけです*2。

*2　こういう連載記事を書いているのだから、さぞかし著者は数学の得意な人だろう、と思われるかもしれません。しかし、私はドイツ文学をやりたくて文学部に入った人間です（なのに、第二外国語はフランス語を選択し、結局、哲学科心理学専攻に進みました……というのは余談ですが）。高校時代、数学の実力テストで100点満点中たったの17点しか取れなかったという輝かしい記録を持っているほど数学が苦手でした。それでも、東京大学やお茶の水女子大学で情報やアルゴリズムの授業を担当させてもらっているということは、純粋な数学は別として、道具としての数学はそれほど難しくないということなのでしょう。また、苦手だったからこそ、「どこでつまづくか」がよく分かっているつもりです。

　実は、

線形代数にしても、微分法にしても、結局のところ四則演算をやっているだけ

なのです。ただ、何らかのパターンに従って計算するときに、いちいち「これらの値を足して、あの値で割って……」と、くどくど言うのが面倒なので、ちょっと変わった記号を使って簡潔に書くだけのことなのです。

　そういうわけで、今回は四則演算を出発点として、「中学／高校で学ぶ数学の基本」からおさらいしていきましょう。既にお気付きだと思いますが、一歩ずつ皆さんに語りかけるように進めていくので、「お話のペースが遅い」と感じる人がいるかもしれません。しかし、何かをマスターするための最短ルートは「ゆっくりやる」ことです。音楽やスポーツを習ったことのある人は、ゆっくりと正確にやるのが最良の方法だと教わったことがあるでしょう。それは数学でも同じです。「自分が思っている自分のペース」は意外に速いものです。「回り道だ」とか「無駄だ」とあまり思わずに、ゆっくりとかみくだき、きちんとおなかの中に収めるように心がけるようにしましょう（食べやすくて、消化のよい説明を心がけます！）。

　各項目には「目標」と「解説」と「練習問題」があります。「目標」を既に理解している人は、次の解説を読む必要はありません（でも、意外な発見があるかもしれないので、ぜひとも読んでみてください）。「練習問題」は必須ではありませんが、手を動かしてみたり、考えてみたりすることは、知識を確実に身につけるのに役立ちます。図解や式の変形が複雑になる場合には簡単な動画も用意してあります。動画では一歩ずつ手順を追いかけているので、すんなりと理解できない場合に参照してみてください。

四則演算のルールをざっとおさらい

目標

　今回の目標は、四則演算のルールの確認です。「ハードルはできるだけ低く」をモットーにしてお話を進めるので、少しお付き合いください。

同じ数を何回か足す計算は、掛け算で表せる
同じ数を何回か掛ける計算は、べき乗（詳細後述）で表せる
計算には優先順位があり、かっこで囲んだ計算が優先される

　取りあえず、最低限の基本ということで、これだけを確認しておきましょう。これらのルールを確認した後、機械学習で使われる例として、「距離を求める」ための計算を見ていきます。

解説

　目標に掲げたルールは、いくら数学が苦手な人でもなんとなく覚えているでしょうし、無意識に使っていることと思います。しかし、あらためて意識に上らせておくと、これからの学びが驚くほどスムーズになります。この連載のサブタイトルには「中学／高校数学のキホン」とありますが、まずは小学校の算数（四則演算：足し算／引き算／掛け算／割り算）から始めます。目標に掲げたルールを実例で確認しておきましょう。

ルール1　同じ数を何回か足す計算は、掛け算で表せる

　あまりに簡単だと、読むスピードが速くなりすぎてしまうので、穴埋め問題もやりながら着実に進めていきましょう。□の中には何が入るでしょうか。

　はい、答えは4ですね。3を4回足しているので、3 × 4です。これらの式を見ると、掛け算は「足し算の延長」で、「決まったパターンの足し算を簡単に書く方法」と考えることもできます。上の例は簡単すぎるので、掛け算のありがたみが分かりませんが、例えば、3を100回足すとしたらどうでしょう。

　このように書くのは、足し算が多すぎて面倒ですね（あまりにも面倒なので途中を省略してしまいました。数学的にちょっとイジワルなことを言うと「⋯ 」の部分があいまいです）。それより、3 × 100と表した方がはるかに簡単で、正確です。

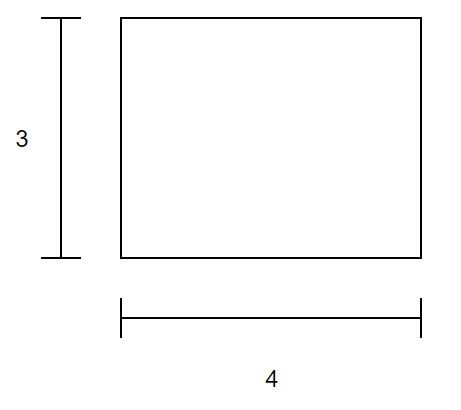
　さらに、掛け算は面積を求めるためにも使われます。図1のような長方形の面積は3 × 4＝12となります。4 × 3でも結果は同じです。

図1　掛け算は面積の計算にも使われる

　割り算も、「0で割っちゃダメ」というルールはありますが、「掛け算の延長」として捉えることができます。割り算は、逆数*3を掛けると考えればいいというだけのことです。

*3　例えば、元の数の逆数は、

という分数で表されます。

　例えば、3の逆数は、

です。

　例えば、6 ÷ 3という割り算は、どういう逆数の掛け算になるでしょうか？

ですね。

　さらに、6から3を何回引けるかということだと考えれば、割り算は「引き算の延長」にすぎないともいえます*4。その引き算は「負の数を足すこと」と考えれば、「足し算の延長」になります。数学的に細かな議論はさておき、結局は全て「足し算の延長」だと捉えることもできますね。

*4　6 ÷ 3という割り算の場合、6－3＝3、3－3＝0というように6から3が「2回引ける」ので、やはり答えは2となります。

　全くの余談ですが、電卓を使って0で割り算をすると、当然のことながらエラーが表示されます。しかし、初期の電卓には、0で割るとパニックを起こしたかのように数字がめまぐるしく変わるものがありました。おそらく、「元の数」から「割る数」を何回引けるか、を数えていたのでしょう（0を引いても元の数のままなので、いつまでたっても計算が終わらず、回数だけがどんどん増えていくというわけです）。私が小学生の頃、それを偶然発見し、1 ÷ 0などを計算させて、延々と数字が変わるのを飽きずに眺めていた記憶があります（残念ながら、その不思議体験は数学的才能の開花には結び付きませんでしたが）。

　ちなみに、先ほどは長方形の面積を計算しましたが、それ以外の「面積の計算」には積分という計算方法を使うケースもあります。積分では、足し算と掛け算を使います。例えば、（本連載で解説する）確率の計算（＝確率分布のグラフの面積を求める計算）などには積分が使われます。

　また、（本連載で解説する）微分という計算方法では、引き算と割り算を使います。微分は「変化率を求める」ことと考えられます。

　難しそうに見えますが、結局は四則演算なのです。

　では、次のルールに進みましょう。今度は中学校にレベルアップします。

ルール2　同じ数を何回か掛ける計算は、べき乗で表せる

　念のための確認ですが、「2の3乗」は「にのさんじょう」と読みますね。

　これも、穴埋め問題で確認しておきましょう。□の中には何が入るでしょうか。

　簡単ですね。答えは6です。5を6回掛けているので、5の6乗ということになります。べき乗は四則演算そのものには含まれませんが、「掛け算の延長」なので四則演算に毛が生えた程度のものと考えればいいですね。掛け算のことを「乗算」とも呼ぶのはご存じでしょう。そのことからも「6乗」なら「6回掛ける」ことだというのが分かります。

　負の数を2乗すると正の数になることも重要です。

　「何の何乗」における「何乗」に当たる数のことを指数（しすう）と呼びます。4²であれば、指数は2です。

　また、今は覚える必要はありませんが「何の」に当たる数のことを底（てい）と呼びます。4²であれば、底は4です。

ルール3　計算には優先順位があり、かっこで囲んだ計算が優先される

　最後は、計算の順序に関するルールです。このルールに関しては、もう少し詳細に記しておきましょう。

足し算や引き算よりも、掛け算や割り算が優先する
掛け算や割り算よりも、べき乗が優先する
かっこで囲んだ計算が優先する

　足し算や掛け算などの記号は、一般に演算子と呼ばれます。演算子は優先順位が同じであれば、たいていは「左から右へ」と計算していきますが、べき乗は「右から左へ」（「上から下」と言った方がいいでしょうか）と計算します。優先順位の異なる演算子が式の中にある場合は、優先される計算の方を先に行います。優先順位を上げたいときにはかっこで囲みます。幾つかの例で確認しておきましょう。