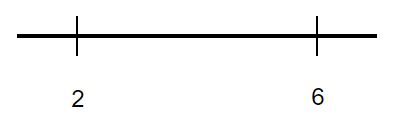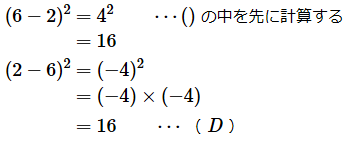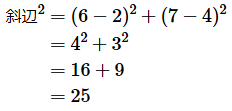AI・機械学習のための数学超入門 ― 前提知識は四則演算だけ！：AI・機械学習の数学入門（3/4 ページ）

機械学習の数学は難しい!? そう思っている人はここから学んでみよう。本連載では、小学校で習う「四則演算（足し算／引き算／掛け算／割り算）」を使って、機械学習の数学をできるだけ分かりやすく簡単に説明していく。だからサブタイトルは「― 中学／高校数学のキホンから学べる」。今回は距離を求める中学数学をおさらいする。

[羽山博，著] PC用表示関連情報

LINE

Hatena

前のページへ | 次のページへ

距離を求める　～　機械学習で使われる数学（1）

　四則演算のルールを確認しただけでは、機械学習のどういう場面で役に立つのかが分からないので、簡単な利用例として、距離の計算方法を見ておきましょう。

　機械学習では、ほとんど全ての手法で距離を求める計算が使われます。例えば、最適な値を求めるために（仮に定めた最適な値と）各データとの距離を小さくしていく（これによって「仮に定めた最適な値」は徐々に「実際の最適な値」へ近づいていきます）、という場合に「距離の計算」が必要になります。最適な値と各データとの距離は「誤差（error）」と捉えることもできます。

直線上の距離を求める

　図3のような数直線では、2という位置と6という位置の距離は引き算で求められます。つまり、6－2という引き算になるので答えは4です。一方、2－6という引き算もできます。そうすると答えは－4という負の値になります。

図3　直線上の距離を求める

　距離は正の値なので、どちらからどちらを引いても正になるようにしたいですね。そのような値を絶対値（＋や－が付かない値）と呼び、|～|で囲んで表します。

　なので、距離は4になります。

　ただ、絶対値を取り扱うためには元の値が正の場合と負の場合に分けて考える必要があり、計算上の取り扱いが面倒です。そこで、ちょっとしたワザを使って計算を簡単にします。

　1ページ目でお話したように、負の値を2乗すれば正の値になります。その後で、正の平方根（＝正の数の「平方根」）、つまり、√（ルート）を求めれば、絶対値になります。なお、「平方根」の意味については実際の計算を見ながら説明します。

　まず、「6－2」と「2－6」という引き算の結果である「4」と「-4」を2乗してみましょう。

（D）負の数 × 負の数は正の数になる（＝負の数を2乗すれば正の数になる）

　となり、いずれも16という値になります。その後で、正の平方根*5を求めます。

*5　平方根（square root、ルート）とは、「2乗する前の値」のことです。

　例えば「16」は、何かを2乗した値です。何を2乗したら16になるでしょうか？

　答えは4と－4です。4²も(－4)²も16ですよね。つまり「2乗する前の値」は4と-4になります。これらの平方根のうち、正の方を

のように√（ルート）という記号を使って書きます。負の方は、

と表されます。

　この平方根も中学校の数学ですが、ここではこれ以上詳しくは触れません。

　16の正の平方根は、

なので、ちゃんと4という距離が求められていますね。

　ただし、いちいち√を計算せずに、距離の代わりに「距離の2乗」をそのまま使うことがよくあります。文字式や関数を扱うようになると、2乗のままの方が数式の取り扱いが便利ですし、必要になった時点で√の計算をすればいいので、取りあえずそのままにしておくというわけです（というわけで、平方根については詳しく触れませんでした）。

平面上の距離を求める

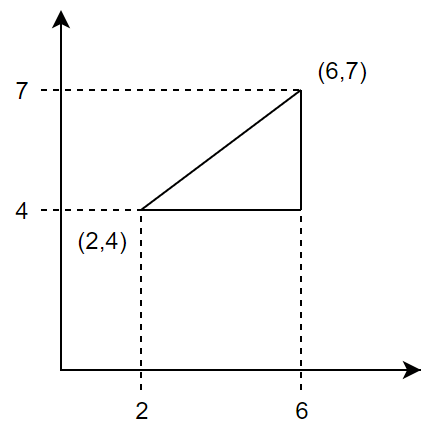
　平面上の点は、横方向（x方向）の値と、縦方向（y方向）の値を組み合わせて、(2,4)のように表されます*6。横方向が2、縦方向が4の位置となります。

*6　このような(2,4)という値の組み合わせ（＝数値などの複数の要素を一列に並べてひとまとめにしたもの）はベクトルと呼ばれ、やはり機械学習でよく使われます。横方向の値と縦方向の値を個別に取り扱うよりも、ひとまとめにして取り扱った方が便利ですからね。

　図4には、(2,4)と(6,7)という2つの点があります。これらの距離を求めてみましょう。

図4　平面上の距離を求める

　(2,4)と(6,7)の距離を求めるということは、図に示された直角三角形の斜辺の長さを求めることにほかなりません。直角三角形の斜辺の長さは、有名なピタゴラスの定理（以下の式）で求められますね。

　底辺も高さも引き算で求められます。つまり、以下のように計算できます。

　斜辺の2乗が25なので、斜辺の長さは√25＝5です。しかし、これについても、いちいち√を求めずに、2乗したままの値を後の計算でそのまま使うことがよくあります。

　この計算過程を分かりやすく解説する動画（音声解説付き）も用意しました！

動画1　「距離（＝斜辺）の計算」を分かりやすく解説*7

*7　「基準となる点」の位置を0（ゼロ）としていますが、この点のことを原点と呼び、一般にO（オー）というアルファベットで表します。OはOrigin（オリジン＝原点）の頭文字です。この例では、原点Oの位置は、x座標の値もy座標の値も0なので、正確に言うと(0,0)となります。

コラム　距離にはいろいろある

　ここで「距離」と呼んでいるものは、ユークリッド距離と呼ばれるものです。実は、数学的には、距離は以下のような性質を満たすものとして定義されています。

点Pと点Pの距離は、0である
点Pと点Qの距離は、点Qと点Pの距離に等しい
「点Pと点Q」＋「点Qと点R」の距離は、点Pと点Rの距離以上である

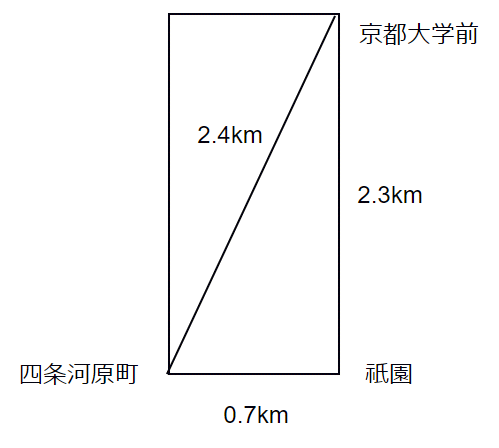
　最後の項目は、要するに点Pから点Rに行くときに点Qに寄り道してもいい、ということです。「以上」ということなので、いわゆる最短距離でなくてもいいわけです。例えば、京都市内の中心部は道路が碁盤の目のようになっていますが、図5のように、その道筋を縦横に通った長さを「距離」としても上の定義に当てはまります。このような距離はマンハッタン距離と呼ばれます（日本なら平安京とか平城京の方がしっくりくるかもしれませんね）。