[活性化関数]Swish関数(スウィッシュ関数)とは?:AI・機械学習の用語辞典
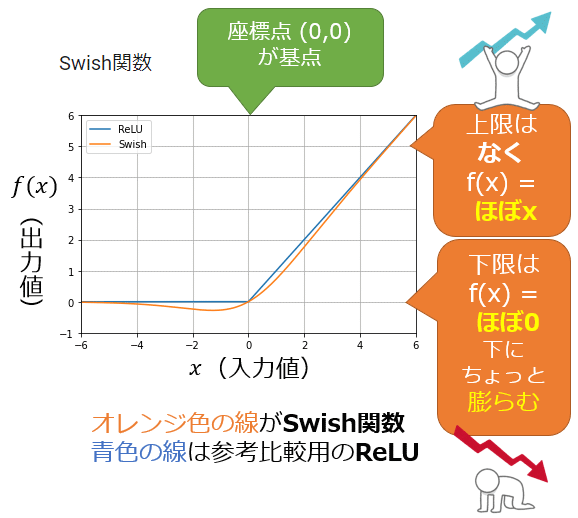
用語「Swish関数」について説明。「0」を基点として、0以下なら「ほぼ0」だが(わずかに「負の値」になる)、0より上なら「入力値とほぼ同じ値」を返す、ニューラルネットワークの活性化関数を指す。類似するReLUの代替として使われる。
用語解説
AI/機械学習のニューラルネットワークにおけるSwish関数(「スウィッシュ」と読む)もしくはSiLU(Sigmoid-weighted Linear Unit、「シルー」と読む)とは、関数への入力値が0以下の場合には出力値がほぼ0(※わずかに負の値になる)、入力値が0より上の場合には出力値が入力値とほぼ同じ値となる関数である。
図1を見ると分かるように、ReLUという活性化関数に非常に似ている曲線を描く(=ReLUをSwish関数に置き換えやすい)が、その曲線が連続的で滑らか(smooth)かつ非単調(non-monotonic)である点が異なる。基点として(0, 0)を通るが、滑らかであるため、いったん下側(マナイス側)に少し膨らむ点が特徴的だ。
現在のディープニューラルネットワークでは、隠れ層(中間層)の活性化関数としては、ReLUを使うのが一般的である。しかし、より良い結果を求めて、ReLU以外にもさまざまな代替の活性化関数が考案されてきている。Swish関数は、その中でも比較的有名な活性化関数の一つである。
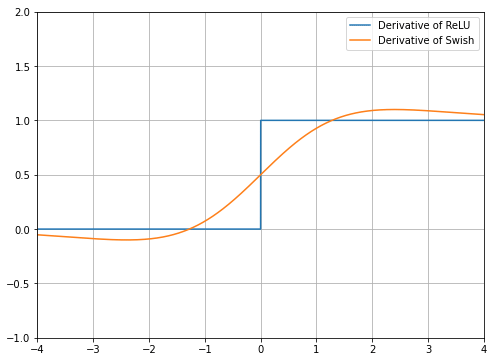
まずは、ReLUを試した後、より良い精度を求めてSwish関数に置き換えて検証してみる、といった使い方が考えられる。2017年の論文「arXiv:1710.05941v1 [cs.NE]」や「arXiv:1710.05941 [cs.NE]」によると、ReLUやReLU派生のさまざまな活性化関数よりも良い精度になりやすい、とのことである。Swish関数の導関数(Derivative function:微分係数の関数)は図2のようになり、ReLUよりも滑らかに変化する、という特徴がある。
この特徴により、ReLUだと0.0と1.0の境界でカクカクとした学習結果となってしまうが、Swish関数ではその問題がなく滑らかな学習結果になる、というわけだ。
主要ライブラリでは、次の関数/クラスで定義されている。
定義と数式
冒頭では文章により説明したが、厳密に数式で表現しておこう。
Swish関数は、標準シグモイド(Sigmoid)関数を内部で用いる。ここでは、標準シグモイド関数をσ(x)(=xを入力とする、「シグマ」という名前の関数)と表現する。数式は以下の通りである。
e(オイラー数)や、それに対応するnp.exp(x)という後述のコードについては、「シグモイド関数」で説明しているので、詳しくはそちらを参照してほしい。
このσ(x)を用いてSwish関数の数式を表現すると、次のようになる。
上記の数式の導関数を求めると、次のように非常にシンプルな式になる。
Pythonコード
上記のSwish 関数の数式をPythonコードの関数にするとリスト1のようになる。なお、オイラー数に関して計算するため、ライブラリ「NumPy」をインポートして使った。
import numpy as np
def sigmoid(x):
return 1.0 / (1.0 + np.exp(-x))
def swish(x):
return x * sigmoid(x)
Swish 関数の導関数(derivative function)のPythonコードも示しておくと、リスト2のようになる。
# ※リスト1のコードを先に記述する必要がある
def der_swish(x):
return swish(x) + (sigmoid(x) * (1.0 - swish(x)))
Copyright© Digital Advantage Corp. All Rights Reserved.