[活性化関数]SELU(Scaled Exponential Linear Unit)とは?:AI・機械学習の用語辞典
用語「SELU(Scaled Exponential Linear Unit)」について説明。「0」を基点として、入力値が0以下なら「0」〜「-λα」(λは基本的に約1.0507、αは基本的に約1.6733)の間の値を、0より上なら「入力値をλ倍した値」を返す、ニューラルネットワークの活性化関数を指す。ReLUおよびELUの拡張版。
用語解説
AI/機械学習のニューラルネットワークにおけるSELU(Scaled Exponential Linear Unit)とは、関数への入力値が0以下の場合には出力値が「0.0」〜「-λα」(※λの値は基本的に約1.0507009873554804934193349852946で、αの値が基本的に約 1.6732632423543772848170429916717なので、つまり「約-1.7580993408473768599402175208123」)の間の値になり、入力値が0より上の場合には出力値が入力値をλ倍した値(※上限はない)となる関数である。
名前から推測できると思うが、ReLUおよびELUの拡張版である。「Scaled(スケールされた)」という言葉の通り、ELU(Exponential Linear Unit)を「λ倍」スケールさせたものである。ただし、ELUのα値が基本的に1.0なのに対し、SELUのα値は上記の通り、基本的に約 1.6733である点にも注意が必要である。
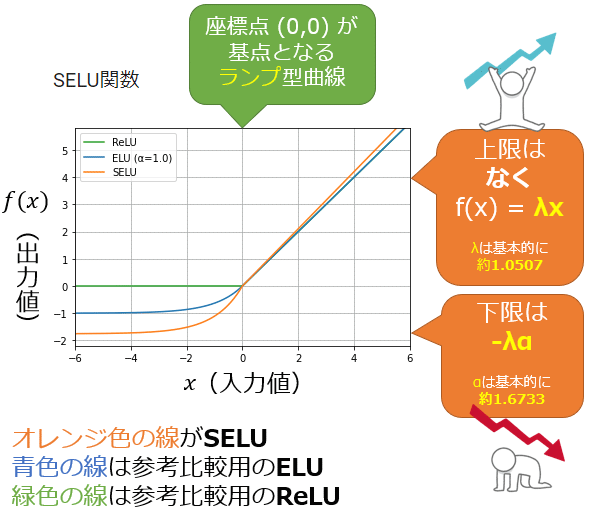
図1は、ELUとSELUの違いを示している(※参考比較用にReLUも載せた)。オレンジ色(SELU)の線の左側が0.0から約-1.7581に向けて下がっており(※比較:青色のELUは-1.0)、右側の直線の傾きが約1.0507になっている点が異なる(※比較:青色のELUは傾きが1.0)。
現在のディープニューラルネットワーク(以下、DNN)では、隠れ層(中間層)の活性化関数としては、ReLUを使うのが一般的である。しかし、より良い結果を求めて、ReLU以外にもさまざまな代替の活性化関数が考案されてきている。ReLUそのものを拡張したLeaky ReLUや、その拡張版であるParametric ReLU(PReLU)などがある。「それらを改善したもの」としてELUがあり、さらにそのELUをスケールさせたバージョンの活性化関数が、(本稿で解説する)SELU(Scaled Exponential Linear Unit)である。
まずは、ReLUを試した後、より良い精度を求めてSELUに置き換えて検証してみる、といった使い方が考えられる。ちなみに、SELUが発表されたのは2017年の論文『Self-Normalizing Neural Networks』(以下、SNN。※詳しくは「arXiv:1706.02515v5 [cs.LG]」/「arXiv:1706.02515 [cs.LG]」を参照)であり、その論文では活性化関数が主題ではなく、標準のFNN(フィードフォワード型ニューラルネットワーク、いわゆる全ての層が全結合のDNN)を改善する「SNN」という新しい手法(method)の紹介が主題であった。そのため、その論文内ではSELUと他の活性化関数との純粋な比較は行われておらず、他の活性化関数と比べた場合のSELUの優位性については不明である(※筆者が検索したところ、論文「arXiv:1804.02763 [cs.LG]」では画像分類タスクにおいて他の活性化関数と比較されている。それによると、特にELUとSELUの比較では、必ずしもELUよりもSELUの方が良いというわけでもないようである)。
主要ライブラリでは、次の関数/クラスで定義されている(※いずれにもλ値とα値は固定となっており、指定できない)。
SNNの論文「arXiv:1706.02515 [cs.LG]」では、基本的な重みの初期化方法(具体的には、平均値が0、分散が1/n[n:入力側の重みの数]となる正規分布。もしくは一様分布や、切断正規分布でもよいため、平均値が0、分散が1/nの切断正規分布である「LeCunの正規分布」を使ってもよい)や、ドロップアウトを使う場合の基本的な方法(AlphaDropout)も提案されている(※正確かつ詳しくは論文を参照してほしい)。
定義と数式
冒頭では文章により説明したが、厳密に数式で表現すると次のようになる。
xが入力データで、f(x)が出力結果である。
x ≦ 0の場合は、f(x)=λ × α × (ex−1)となり(※λは基本的に約1.0507009873554804934193349852946、αは基本的に約1.6732632423543772848170429916717)、
x > 0の場合は、f(x)=λ × xとなる。
上記の数式の導関数(Derivative function:微分係数の関数)を求めると、次のようになる。
SELUはReLU関数と同様に、非連続な関数であり、数学的にはx=0の地点では微分ができない。
SELUの導関数をニューラルネットワーク内で使うために、便宜的にx=0を微分係数αexの方に含めることにする。これにより、次のような導関数が求まる。
Pythonコード
上記のSELUの数式をPythonコードの関数にするとリスト1のようになる。
import numpy as np
SCALE = 1.0507009873554804934193349852946
ALPHA = 1.6732632423543772848170429916717
def selu(x, scale=SCALE, alpha=ALPHA):
return scale * np.where(x > 0.0, x, alpha * (np.exp(x) - 1))
条件分岐(np.where)をコンパクトに記述するために、数値計算ライブラリ「NumPy」を使用した。
x > 0.0は「入力値が0より上か、そうではないか(=0以下か)」という条件を意味する。
その条件がTrueのときは、戻り値としてスケール(scale)された入力値(=scale * x)を返す。なお、scaleという引数が、数式定義のλを表現している。
また、その条件がFalseのときは、戻り値としてスケール(scale)され、α倍の(オイラー数を底とする指数関数−1)(=scale * alpha * (np.exp(x) - 1))を返す。np.exp(x)というコードが、e(オイラー数)を底とする指数関数(exponential function)であるexを表現している。
SELUの導関数(derivative function)のPythonコードも示しておくと、リスト2のようになる。
# ※リスト1のコードを先に記述する必要がある
def der_selu(x, scale=SCALE, alpha=ALPHA):
return scale * np.where(x > 0.0, 1.0, alpha * np.exp(x))
Copyright© Digital Advantage Corp. All Rights Reserved.