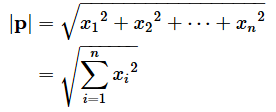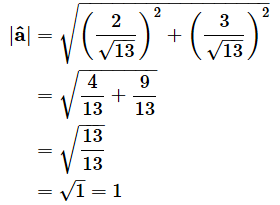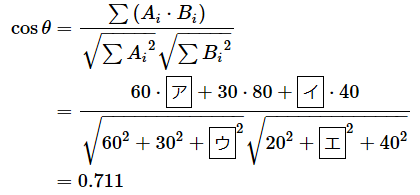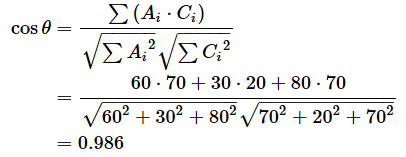[AI・機械学習の数学]ベクトルの基本と類似度の計算:AI・機械学習の数学入門(4/4 ページ)
機械学習では、普通、多くの変数や係数を同時に取り扱う。そのような場合にそれぞれの変数や係数を別々に取り扱うと数式が煩雑になってしまう。ベクトルや行列を利用すれば、複数の値をひとまとめにして取り扱えるので、数式が極めて簡潔になる。今回はベクトルについて、基本的な計算方法を紹介する。
目標【その4】: ベクトルの大きさを求める
ベクトルの大きさ(長さ)とは、始点から終点までの距離です。例えば、ベクトルpの大きさは、絶対値を表す記号と同じ「|」または「||」を使って、以下のように表します。
または
ベクトルの大きさは、連載の第1回で見たピタゴラスの定理を使えば簡単に求められます。
であれば、
となります。次元が増えても同様です。各成分の二乗和のルートがベクトルの大きさになります。
であれば、
となります。
解説【その4】: ベクトルの大きさを求める(さらにコサイン類似度も計算する)
ベクトルの大きさを求める計算はピタゴラスの定理そのものなので、詳しく説明する必要はないと思います。そこで、少しだけ関連のお話をすることにしましょう。前ページの練習問題(2)で、ベクトルの大きさを1にそろえれば、内積がコサイン類似度になるという話をしました。ベクトルの大きさを1にする(単位ベクトルにする)には、ベクトルをその大きさで割ればいいですね。ちょっと例を見てみましょう。
のとき、
です。従って、aと同じ向きで長さを1にしたベクトルをâと表すと、以下のようになります。
なお、^は「ハット」と読みます。â(エー・ハット)の大きさを求めてみましょう。
確かに、âは、aと同じ向きで長さを1にしたベクトルになっていますね。これで、練習問題のところで少し触れたコサイン類似度が求められます。
例えば、ベクトルpとベクトルqのコサイン類似度は、それぞれベクトルの長さで割って求めた単位ベクトルの内積で求められますね。つまり、
となります。cosθ(コサイン・シータ)がコサイン類似度ですが、これは2つのベクトルのなす角度θの余弦関数(コサイン)の値そのものです*3。
*3 本来であれば、各ベクトルをその大きさで割ってから内積を求めた値(上の[A]式)と、内積を各ベクトルの大きさの積で割った値(上の[B]式)が一致することを確認しておく必要があります(実際そうなります)が、それについては省略しています。なお、cosなどの三角関数については機会を見てまた解説したいと思います。
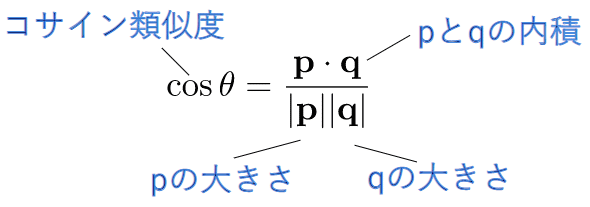
コサイン類似度を表す式の意味を図で確認しておきましょう。
p=(x1,x2,...,xn),q=(y1,y2,...,yn)であれば、以下のような計算で値が求められます。
コサイン類似度は(統計学の一手法である)クラスター分析などで集団の類似度を求めるのに使われます。また、2つの変量の関係を表す相関係数も同じ式で求められます。ただし、相関係数の場合は、各データから平均値を引いた値、つまり平均値を原点としたベクトルを使います。
では、練習問題代わりにコサイン類似度を求める例を見ておきましょう。オレンジの部分をクリックまたはタップすると答えが表示されます。なお、動画での解説も用意しておくのでぜひ参考にしてください。
動画2 コサイン類似度を求める例
例えば、A、B、Cという3種類のテストを3人のメンバーが受験したものとします。それぞれの成績が以下のようになっているとき、テストAとBの類似度、テストAとCの類似度を求めてみましょう。
| A | B | C | |
|---|---|---|---|
| 1 | 60 | 20 | 70 |
| 2 | 30 | 80 | 20 |
| 3 | 80 | 40 | 70 |
| 表1 3種類のテストの結果 | |||
3種類のテストの結果をベクトルで表してみましょう。
A = (60,30, 80 )
B = (20, 80 ,40)
C = (70,20,70)
となります。AとBのコサイン類似度cosθは、以下のようになります。[ア]〜[エ]の部分には数値が入ります。
(答え: [ア]= 20 、[イ]= 80 、[ウ]= 80 、[エ]= 80 )
最後の計算は手計算では面倒なので電卓や表計算ソフトで済ませてしまうといいでしょう。答えは、0.711となりました。では、AとCのコサイン類似度も求めてみましょう。
こちらは結果だけを示しておきます。答えは、0.986となりました。
テストAとテストBよりも、テストAとテストCの類似度の方が高いということが分かりました。ちなみに、この例では値が全て正なので、コサイン類似度は負にはなりません(ちなみにAとBの相関係数は-0.737、AとCの相関係数は0.918です)。
何度も繰り返しますが、ベクトルは複数の値同士の決まった計算を簡単な式で表すのに役立ちます。計算問題はあくまでも、どういうルールで計算をするかを理解するためのものです。式が立てられれば、実際の細かな計算はPCにまかせてしまえばいい、というわけです。
次回は……
今回は線形代数の基本として、ベクトルの考え方と基本的な計算(和・差・内積・ベクトルの長さ)について見ました。ベクトルが使えるようになると多数の値や変数をたった1つの文字で表すことができることが分かったと思います。次回は「行列」についてその基本を学びます。行列を利用すると回帰やニューラルネットワークをより簡潔に表すことができます。
Copyright© Digital Advantage Corp. All Rights Reserved.