あの「モンティ・ホール問題」で当選率33%が66%になる理由が分かり、生き上手になれる「ベイズの定理」の基礎知識:「AI」エンジニアになるための「基礎数学」再入門(10)
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回は「ベイズの定理」について分かりやすい図を交えて解説します。
AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す本連載『「AI」エンジニアになるための「基礎数学」再入門』。前回は「確率・確率分布」について学びました。今回のテーマである「ベイズの定理」は、そのもう少し高度な内容といえます。ぜひ、前回記事も併せてお読みください。
ベイズってどんな人?
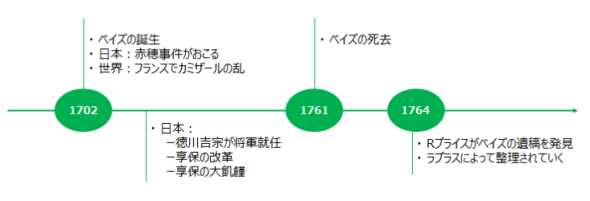
トーマス・ベイズ(Thomas Bayes)は1702〜1761年に実在したイギリスの人物です。彼の肩書は異色で、牧師でありながら数学者でもあります。そんな彼は「神の存在を方程式で説明できる」と主張したそうです。ベイズは牧師として活動する傍ら研究を重ね、後に解説する「ベイズの定理」を含む「ベイズ理論」を考案したという偉業を成しています。
ところが、その偉業はベイズの死後である1764年にRプライス(生命保険の創始者の一人)によって発見されました。その後、偉大な物理学者であるラプラスが理論を整理したことによって発展を遂げることになります。そして、現在では多くの科学技術の礎となりわれわれの生活を支えています。
なお、ベイズの生涯については情報が少なく、いまだ多くの謎が残されています。それにもかかわらず、彼の歴史に登場する関連人物は偉大な人物ばかりです。ミステリアスで魅力にあふれる人物といえるでしょう。
余談ですが、「ベイズ理論」を支持する者を「ベイジアン」と呼ぶことがあります。つまり、今回の記事を読むことで、読者の皆さんはベイジアンへの第一歩を踏み出すことになります。
データサイエンティストが避けては通れない「ベイズ理論」とは
ベイズ理論全体を知ろうとすると、範囲が非常に広く、今回の記事には収まり切りません。そこで今回は導入部分だけにとどめます。
一般的な統計学(頻度論)は「客観確率」を扱います。一方、ベイズ理論は「主観確率」を扱います。ここでは端的に「一般的な統計学とは真逆の考え方をする」と捉えてください。
| 頻度論 | ベイズ理論 | |
|---|---|---|
| 原因 | 固定されたものとして考える | 変動するものとして考える |
| 結果 | 変動するものとして考える | 固定されたものとして考える |
「ベイズ理論」は一般とは真逆の考え方をすることから暗い歴史があります。フィッシャーやネイマンといった「頻度論」の派閥から弾圧されたのです。
しかし、研究が進むにつれてその有用性に対する理解は徐々に広まっていきました。また、ベイズ理論を応用したアルゴリズムは計算コストが高価なことが多く、計算技術の発達に伴って応用ケースが増えていきました。
以上のことから、現代におけるベイズ理論は一般的なものになり、広く応用されています。古くは、ラプラスが土星の質量をベイズ理論から見積もりました。また、第二次世界大戦時には暗号解読にも応用されていたそうです。
最近では、スパムメール診断(ベイジアンフィルター)や医療診断などに応用されています。この他にもわれわれの身近にはベイズ理論が応用された結果がたくさんあります。機械学習のアルゴリズムも同様です。それ故、ベイズ理論を学ぶことはデータサイエンティストにとって避けては通れない道なのです。
上手に生きていく上でとても大切な「ベイズの定理」とは
「ベイズの定理」はベイズ理論を構成する基本定理です。「ベイズ理論=ベイズの定理」ではないことに注意しましょう。基本原理なので、「ベイズの定理を理解すること」は「ベイズ理論を理解すること」への第一歩です。以降では「ベイズの定理」について詳しく解説します。
ベイズの定理を端的に言い表すと、これを使えば「過去にさかのぼって原因を探ることができる」といったものです。われわれが目の当たりにするものは全て結果です。しかし、その結果が引き起こされた理由(原因)を考えることは上手に生きていく上でとても大切なことです。
このように役に立つベイズの定理を、次章では理解に必要な材料とともに詳しく解説します。
ベイズの定理の基本
条件付き確率
ベイズの定理を理解するには、まず「条件付き確率」を知る必要があります。「条件付き確率」とは、その名の通り「ある条件が付いた場合の確率」を考えるものです。
条件付き確率は次のように書き表します。
P(事象|条件)
とある感染症の「感染者」とその「検査」についての例を挙げますので、少しずつ慣れていきましょう。
「感染者」は人口の10%
→ P(感染)=0.1
「感染者」が検査で「陽性」反応が出る確率(感度)は90%
→ P(陽性|感染)=0.9
「非感染者」が検査で「陰性」反応が出る確率は(特異度)は90%
→ P(陰性|非感染)=0.9
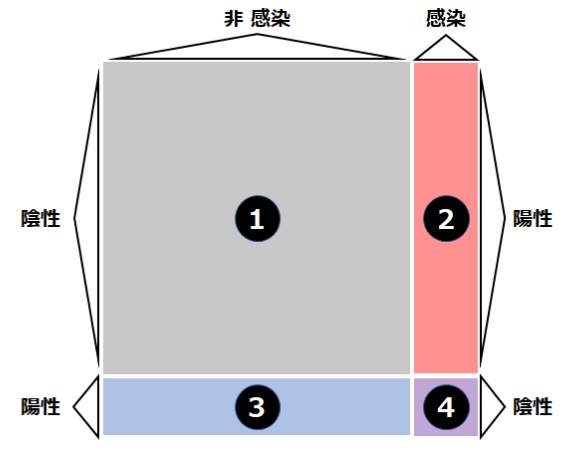
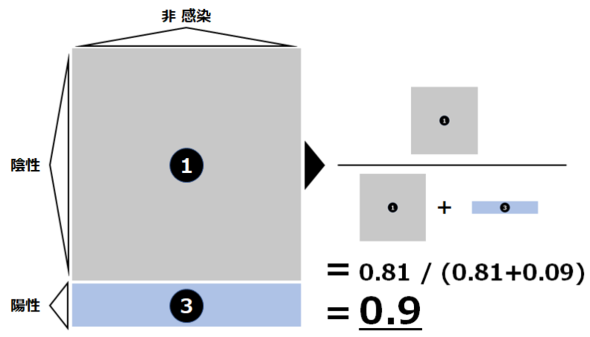
このように少々ややこしいのですが、四角形を描いて整理すると分かりやすくなります。
各領域の面積は次の通りです(後の計算に使います)。
- 【1】0.9 x 0.9 = 0.81
- 【2】0.1 x 0.9 = 0.09
- 【3】0.9 x 0.1 = 0.09
- 【4】0.1 x 0.1 = 0.01
条件付き確率は、この場合、次のものがそれに当たります。
感染者が検査で陽性反応が出る確率(感度)は90%
→ P(陽性|感染)=0.9
非感染者が検査で陰性反応が出る確率は(特異度)は90%
→ P(陰性|非感染)=0.9
それぞれ何が90%なのか四角形を通して確認します。
- 感染者が検査で陽性が出る確率(感度)は90%
まずは四角形から感染者に該当する部分だけ取り出します。この部分だけに注目すると、陽性の割合が全体の90%を占めています。つまり、「P(陽性|感染)=0.9」はこの図のようなことを表しています。
- 非感染者が検査で陰性が出る確率は(特異度)は90%
まずは四角形から非感染者に該当する部分だけ取り出します。この部分だけに注目すると、陰性の割合が全体の90%を占めています。つまり、「P(陰性|非感染)=0.9」はこの図のようなことを表しています。
このように、「条件付き確率を考える」ということは「四角形を限定した場合の面積割合を考える」ということだと分かります。
ベイズの定理
準備が整ったので、早速ベイズの定理について学んでいきましょう。まずは数式をご覧ください(※因、果はそれぞれ、「因果関係」の「因」と「果」)。
P(果|因)P(因)=P(因|果)P(果)
先ほどの例を使って具体化してみます。
- 因:感染していること
- 果:陽性反応が出ること
→ P(陽性|感染)P(感染)=P(感染|陽性)P(陽性)
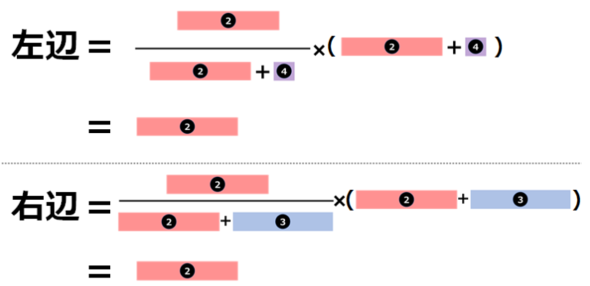
まだ少し難しく感じるかもしれませんが、これは四角形で考えるとごくごく当たり前のことを表していることが分かります。
このように、両辺は共に【2】のことを表しており、「1=1」のように当たり前のことを示しているのが分かります。
ここで定理の右辺に注目して見ましょう。「P(感染|陽性)」はすなわち「陽性反応が出た場合に真に感染している確率」です。これはまさしく過去にさかのぼって原因を探ることに違いありません。これはわれわれにとって非常に興味深い情報となります。
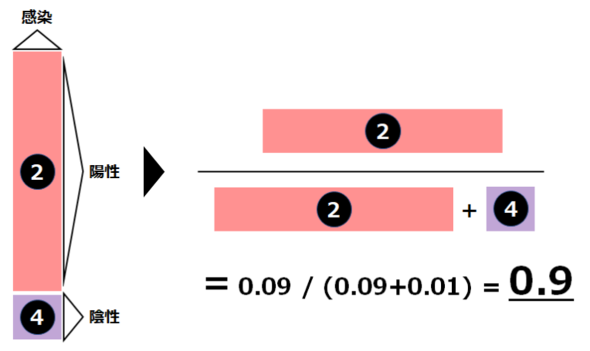
計算してみましょう。
ベイズの定理を用いた結果、「陽性反応が出た場合に真に感染している確率」は50%であることが分かりました。皆さんはこの50%という数字をどう感じましたか? 私は当初この計算結果に対して、感度・特異度ともに90%という数字だったことから「意外に低い」と感じてしまいました。
このように、ベイズの定理はわれわれにとって有益な情報や意外性のある発見をもたらしてくれます。
ベイズの定理の応用「モンティ・ホール問題」
最後に確率論かいわいで有名な話を紹介して終わりにします。
皆さんは、「モンティ・ホール問題」をご存じでしょうか。これは、とあるクイズ番組を題材にした話で、次のような状況が設定されています。
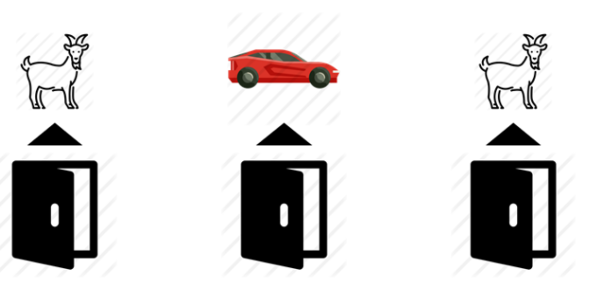
- プレイヤーの前に閉じられた3つのドアが用意される
- そのうち1つの後ろには景品(アタリ)があり、残りの2つはハズレ
- まずプレイヤーがアタリだと思うドアを選択する
→この時点ではドアはまだ開けない - 事前にどのドアが当たりかを知っている司会者が、残った2つのドアのうち、外れのドアを開ける
→残った2つがどちらもハズレの場合はランダムに一方を開ける - 司会者はプレイヤーに「最初の選択を変えてもいい」と伝える
このとき、プレイヤーは「最初に選んだドア」か「もう一方のドア」のどちらを選択すべきか? という問題です。
結論は下記です。
- 最初に選んだドアを選択 → 当選率33%
- もう一方のドアを選択 → 当選率66%
なぜそうなるのでしょうか。気になる方はぜひ「ベイズの定理」を用いて考えてみてください。この定理の面白さをさらに深く知ることができることでしょう。
おわりに
繰り返しになりますが、今回学んだ「ベイズの定理」は機械学習アルゴリズムの中で多くのものに応用されているものです。面白さもさることながら、実用性もあります。さらなる学習を進めたい方は、ぜひ「ベイズ理論」や「ベイズ統計」といったワードに該当する専門書を読んでみてください。
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
 綱引きに蛇口当てゲーム?! 楽しく学ぶベイズフィルターの仕組み
綱引きに蛇口当てゲーム?! 楽しく学ぶベイズフィルターの仕組み
残念ながら、メールの世界では迷惑メールの送信を根絶することがまだできていません。そのため、受信時に必要なメールとそうでないメールを判別する必要があります。今回は単語の頻出度合いから必要なメールかどうかを判別する「ベイズフィルター」(ベイジアンフィルター)の動作理論と実装上の工夫を2回に分けて解説します(編集部) Apache Mahoutの使い方:テキスト分類のアルゴリズムを活用する
Apache Mahoutの使い方:テキスト分類のアルゴリズムを活用する
機械学習は古くからある情報処理のアルゴリズムの総称です。これをApache Hadoop上で実施する際のフレームワークの1つがApache Mahoutです。本稿ではApache Mahoutを使った機械学習の初歩を学んでいきます。 10万点以上の点群位置合わせ問題を2分で解く 金沢大学の広瀬修氏がアルゴリズムを考案
10万点以上の点群位置合わせ問題を2分で解く 金沢大学の広瀬修氏がアルゴリズムを考案
金沢大学の助教である広瀬修氏は、点群位置合わせ問題を解くための新たなアルゴリズムを考案した。点群位置合わせ問題をベイズ統計学に基づいて定式化することで、最高精度の解を最小計算時間で見つけることに成功したとしている。