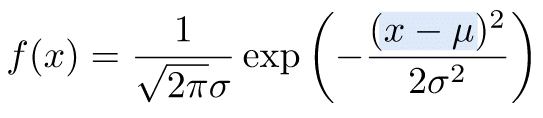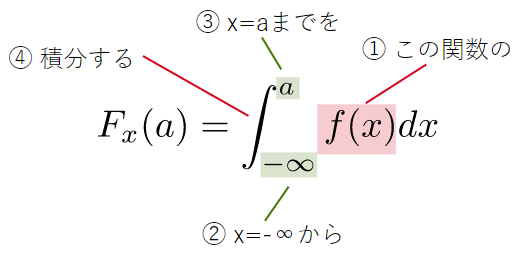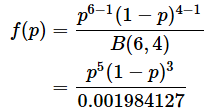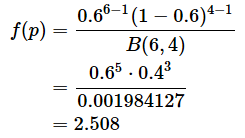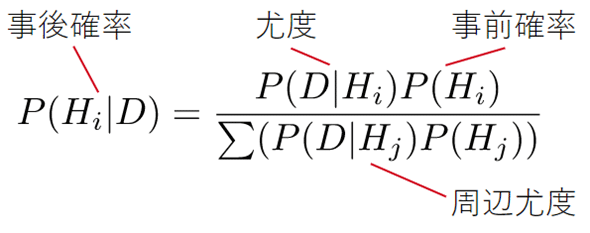[AI・機械学習の数学]正規分布とベータ分布、確率分布とベイズ統計の関係を理解する:AI・機械学習の数学入門
統計学や機械学習で使われるさまざまな確率分布のうち、連続分布の例として正規分布とベータ分布について見ていく。また、最近主流になりつつあるベイズ統計の関係についても簡単に紹介する。
前回は、「確率の分布とはどのようなものか」について説明し、離散分布の例としてベルヌーイ分布と二項分布を学びました。今回は、連続分布の例として正規分布とベータ分布を紹介します。併せて、ごく簡単にではありますが、事前分布や事後分布など、ベイズ統計に関する話題についても触れます。具体的には、前回と次回で以下のようなトピックを扱っています。
前回の内容を読んでいない場合は、先に一読することをお勧めします。セットでまとめて読みやすいように、今回は各節や図、脚注などの番号は、前回の番号からの続きとなっています。
目標【その4】: 正規分布とは
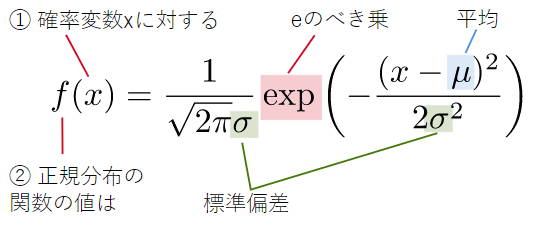
正規分布とは、以下のような式で表される分布です(ガウス分布とも呼ばれます)。正規分布は身長の分布や誤差の分布など、平均値のところが山の「頂上」で、左右対象に「裾野」が広がっている分布です(後で示すグラフを見れば一目瞭然です)。
べき乗の部分が小さく、見づらいので、enをexp(n)のように表して、以下のように書くこともあります。
この式の中のμは平均、σは標準偏差を表します。μは「ミュー」と読み、σは「シグマ」と読みます。これはギリシア文字Σの小文字です。また、πは円周率(3.141592...)で、eは自然対数の底と呼ばれる値(2.718281...)です。πやeは定数なので、正規分布の母数はμとσであることが分かります。
なお、μ=0,σ=1である正規分布を標準正規分布と呼びます。
解説【その4】: 正規分布とは
正規分布を表す式はかなり複雑ですね。取りあえず、どういった式かを確認しておきましよう。例によって指さし確認をしながら意味を確認していくといいでしょう。また、動画の解説も用意してあるので、式の意味を丁寧に追いかけたい方はぜひ視聴してください。
動画2 正規分布
この式では、標準偏差を表すσという文字が新しく登場しました。標準偏差とは、分布のばらつきを表す値です(後で掲載するグラフを見れば一目瞭然です)。分布のばらつきを表す値としては分散も使われますが、一般に、標準偏差=√分散となっているので、分散はσ2と表されます*4。
正規分布の式は一見複雑ですが、ざっくりと捉えると意味が分かりやすくなります。要するに定数のべき乗の形になっています。そこで、定数は気にせず、べき乗の部分に注目しましょう。
穴埋めでイメージを確認してみましょう。オレンジ色の部分をタップまたはクリックすると答えが表示されます(最初の2つは数字が入り、後ろの4つは「大きく」または「小さく」のいずれかが入ります)。
というわけで、図8のアミカケの部分を見ると、xの値が平均値μに等しいと、x−μ= 0 なので、eのべき乗の部分が 0 になります。一方、xの値が平均値μから離れるほど、x−μの絶対値が 大きく なり、eのべき乗の部分が0よりも 小さく なることが分かります(絶対値は大きくなりますが、マイナスが付いているので)。ということは、xの値が平均値に近ければこの関数の値が 大きく 、平均値から離れるほど関数の値が 小さく なることが分かります。
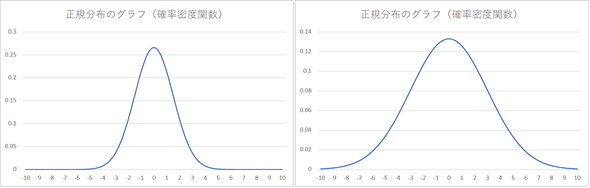
では、実際そうなっているかどうか、正規分布のグラフを見てみましょう(図9)。ここでは、「平均μ=0、標準偏差σ=1.5」と、「平均μ=0、標準偏差σ=3」の正規分布を考えてみます。
確かに、平均値が山の「頂上」になっており、左右対称に「裾野」が広がっていることが分かりますね。また、標準偏差が大きいと「裾野」の方にも値が散らばっている(ばらつきが大きい)ことが分かります。確率変数を意味する横軸の目盛り(……、0、1、2、……)は飛び飛びになっていますが、確率変数の値は連続した値になってつながっていることにも注意してください。例えば、横軸の0と1の間はいくらでも細かく分けられます。つまり、「すき間」なく値が存在するということです。身長などもそういった値ですね。測定機器に精度の限界があるので、170.0cm、170.1cm……という飛び飛びの値が得られますが、精度が限りなく上げられるなら、170cmと171cmの間はいくらでも細かく分けられます。
「連続」の定義を数学的に表現すると話が難しくなるのでこれ以上は触れませんが、二項分布(前回の図6を参照)のような棒グラフと図9のスムーズなグラフの違いからも直感的に理解できると思います。このように確率変数の値が連続した値になっている分布を連続分布と呼びます。
確率密度関数と累積分布関数
正規分布に限らず、連続分布には扱いに気をつけないといけない点が幾つかあります。具体例で見てみましょう。ちょっと値を変えて、平均μが60、標準偏差σが10の正規分布を考えてみます。
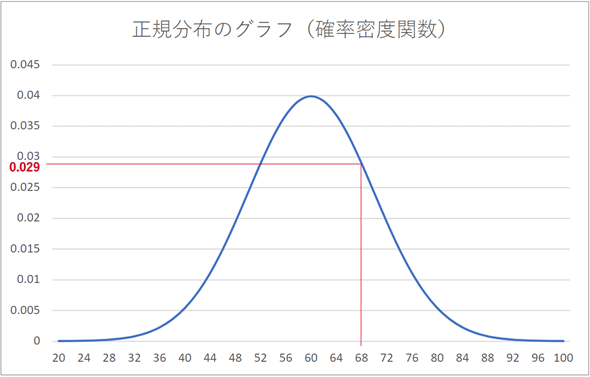
このグラフを描くと以下のようになります。グラフの横軸(確率変数の値)は20〜100までしか表示していませんが、正規分布の確率変数は-∞〜∞の値を取ることに注意してください(従って、試験の成績のように0〜100の値を取るような分布は、厳密には正規分布に従っているとはいえません)。
x=68のとき、f(x)の値は0.029になります。この値は、【目標】のところに示した式に値を代入すれば求められますが、さすがに手計算は面倒ですね。Excelで「=NORM.DIST(68,60,10,FALSE)」と入力すれば簡単に求められます。また、Pythonなら、
from scipy import stats
stats.norm.pdf(x=68,loc=60,scale=10)
# 出力例: 0.028969155276148274
で求められます(pdfは確率密度関数を意味する「probability density function」の略です)。
ここでは、ExcelやPythonの詳細については説明しませんが、手計算での練習問題がこの後は出てこないので、ExcelやPythonが使える環境にある方は、練習問題代わりに上の例を試してみてください(空のGoogle Colaboratoryノートブックを使えば無料かつWeb上でPythonコードを実行して試すことができます)。
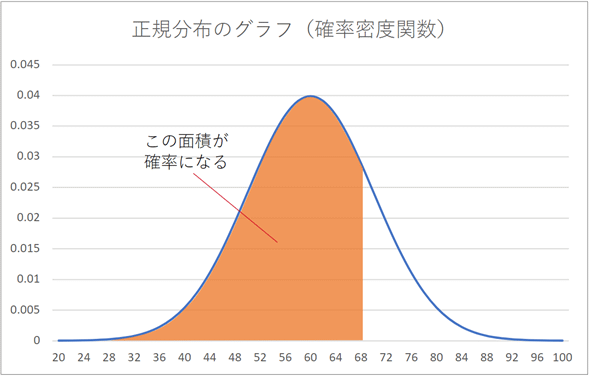
さて、上で述べましたが、x=68のとき、f(x)の値は0.029になりました。前掲した図10のグラフを見てみると、xが68であるときの正規分布の確率が0.029であるように思われるかもしれません。しかし、この0.029という値は、確率変数がちょうど68である確率ではないということに注意してください。この値は確率そのものではなく、確率密度と呼ばれる値で、いわばその確率変数が現れるもっともらしさを表しています(実際、統計学では「尤度」として扱われます)。そういうわけで、目標のところに掲載した正規分布の式(関数)は確率密度関数と呼ばれます*5。
*5 ベイズ統計では、離散分布の場合と同様(前回の「コラム 尤度について」を参照)、確率密度関数の値が尤度として扱われるので、θを母数とし、確率変数をxとすると、尤度は、
で表されます。ちなみに、最頻値(確率密度関数の山の最も高い位置)は、母数としていちばん「それらしい値」であると考えられます。このように、尤度の最も高い値を母数の推定値とすることを最尤推定法と言います。正規分布の場合、平均値が最尤推定値となります(ただし、ベイズ統計では最尤推定法は使いません)。
連続分布での確率を求めるには、確率変数が何らかの値から何らかの値までを取る場合を考えます。例えば、xが68までである確率は、図11に示すオレンジ色部分の面積にあたります。
面積を求めるには積分という計算を行います。高校の数学で微分の次に登場する単元ですが、今のところ計算方法を詳しく知らなくても問題ありません。が、書き方と意味だけは確認しておきましょう。例えば、正規分布の確率密度関数f(x)をx=−∞〜aまでを積分することを、以下のように表します。
∫は「インテグラル」と読みます。これは合計(Sum)を表す「S」を縦に引き伸ばしたような形になっています。上の式の右辺なら「インテグラル、マイナス無限大からaまでのエフエックス、ディーエックス」のような読み方になります。ここでは、関数を積分するとx軸とグラフで囲まれた部分(図12のオレンジ色の部分)の面積が求められ、それが確率になっているということだけ理解しておいてください。
確率密度関数を積分すると、その上限(上の例ではa)までの累積確率P(x≤ a)が求められます。では、x=68までを積分して面積(=確率)を求めてみましょう。以下のように、f(x)のところに正規分布の確率密度関数を書いてチョチョイと積分すればいいですね……などと言うのは簡単ですが、手計算でやるのは現実的ではありません(そもそも積分の計算方法を本連載ではまだ説明していませんし、高校数学の知識では正規分布の確率密度関数を積分するのは無理なので)。
というわけで、ここはパソコンを使いましょう。Excelなら「NORM.DIST(68,60,10,TRUE)」と入力すれば求められます。この関数はすでに紹介しましたが、最後の引数が「FALSE」なら確率密度を求め、「TRUE」なら累積確率を求めることになります。Pythonなら、
from scipy import stats
stats.norm.cdf(x=68,loc=60,scale=10)
# 出力例: 0.7881446014166034
で求められます(cdfは後述する累積分布関数を意味する「cumulative distribution function」の略です)。結果は、0.788になるはずです。つまり、x=-∞からx=68までの確率は0.788であるというわけです。
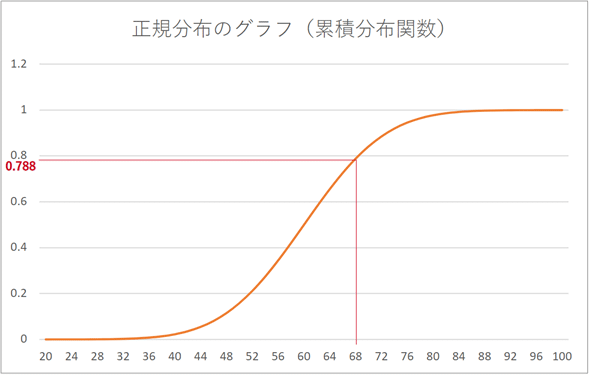
ところで、確率密度関数を積分した式も、やはり関数になっていることに気付くと思います。前掲の図12ではFx(a)と表しました。このような累積確率の関数を累積分布関数と呼びます。
正規分布の累積確率関数のグラフは図13のようになります。これは、x=aまでの累積確率(面積)の値をグラフにしたものです。x=68に対するグラフの値が0.788になっていることが確認できますね。
コラム 中心極限定理
統計学で正規分布がよく使われる背景には中心極限定理と呼ばれる定理があります。これは、元の分布がどのような分布であっても、そこからサンプルを取り出して合計を求めることを何度も繰り返すと、それらの合計の分布が正規分布に近づくという定理です。もとの分布の平均をμ、分散をσ2とすると、合計の分布は平均がnμ、分散がnσ2の正規分布に近づきます。
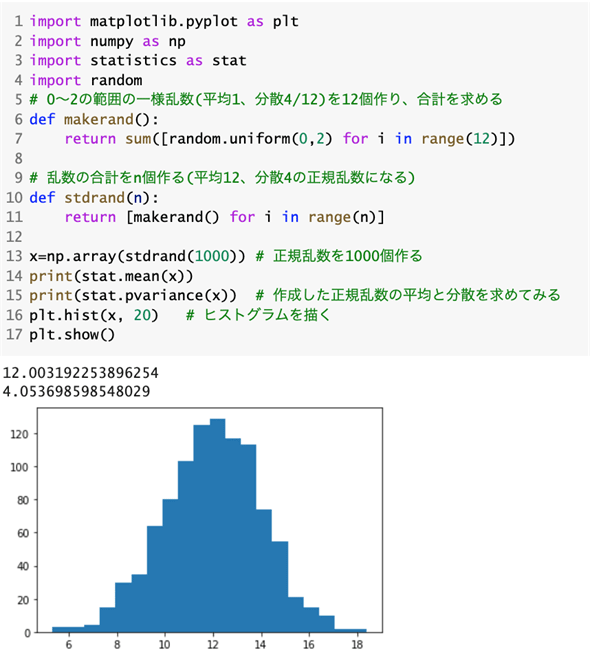
以下の例は、簡単なシミュレーションで試してみた結果です。プログラムの詳細については省略しますが、0から2の範囲の一様分布(μ=1,σ2=4/12)から12個のサンプルを取り出して合計したものを1000個作り、その平均と分散を求めたものです。併せてヒストグラムも描いてあります。
得られた結果の平均値は12.00となり、12(nμ)に近い値になっていることが分かります。また、分散も4.01となり、4(nσ2)に近い値になっていることが分かります(これらの数値は実行のたびに変わりますので、読者が実行しても全く同じ数値とはなりません)。ヒストグラムも正規分布に近い形になっていますね。
目標と解説【その5】: ベータ分布とは
連続分布の例として、ベイズ統計でよく使われるベータ分布についても紹介しておきましょう。ベータ分布の確率密度関数は、以下のような式で表されます。
この式で、分子のpはある事象が起こる確率、αはその事象が起こった回数、βはその事象が起こらなかった回数で、α、βとも正の整数です。分母はベータ関数と呼ばれる関数です。ベータ関数の詳細については触れませんが、ベータ分布を0から1まで積分したときに累積確率が1になるようにするために使われます。一応、ベータ関数の式を書いておくと、
となります。Γはガンマ関数と呼ばれる関数で、階乗の考え方を0以上の整数だけでなく、複素数の範囲にまで拡張した関数です。
二項分布のところで見たイカサマコインを例に、具体例で見てみましょう。表が出る確率pが確率変数になっていることに注意してください。ただし、α、βとも0ではないので、表、裏とも1回以上出るものとします。例えば、10回コインを投げて、表が6回、裏が4回出たとします。この場合、
となります。B(α,β)は、ExcelのGAMMA関数を使って「=GAMMA(6)\*GAMMA(4)/GAMMA(6+4)」で求めた値です。Pythonなら、
from scipy.special import beta
beta(6,4)
# 出力例: 0.001984126984126984
で求められます。
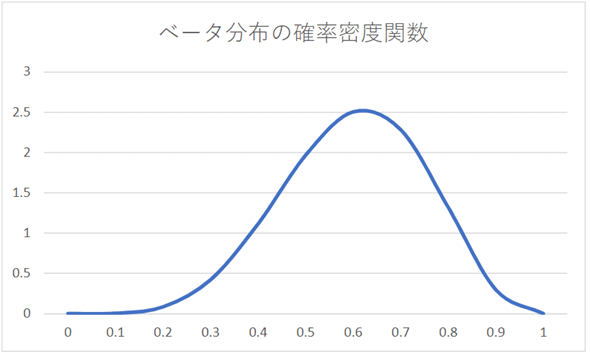
これをグラフ化してみましょう。確率変数はpであることに注意してください。
ベータ分布の最頻値M(グラフの山が一番高くなるところ)は、
なので、この例では、p=0.625のところです。表が6回、裏が4回出る場合、p=0.625が最もそれらしい値(最尤推定値)になるというわけです。
ベータ分布についても、やはり確率密度関数の値は確率そのものではありません。例えば、p=0.6に対する確率密度f(p)は、
となりますが、p=0.6となる確率がちょうど2.508ということではなく、p=0.6になる尤度が2.508であるということです(そもそも、確率であれば1を超えることはありませんね)。
ベータ分布の累積分布関数もやはり積分で求める必要がありますが、これについても手計算では実質的に無理なので、Excelなら「BETA.DIST(6,4,0.6,TRUE)」と入力すれば求められます。ちなみに最後の引数が「FALSE」なら確率密度関数の値が求められます。Pythonなら、以下のように求められます。
from scipy import stats
stats.beta.cdf(x=0.6,a=6,b=4)
# 出力例: 0.48260966399999977
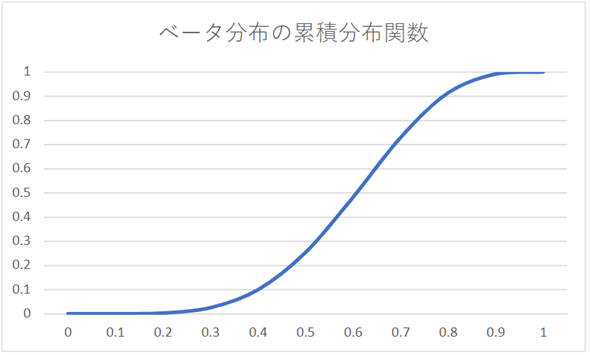
この例では、表が6回、裏が4回出る確率が0.6までである確率は0.483である、ということになります。値の解釈はちょっと難しいですが、表が6回、裏が4回出たときに、表が出る確率が0.6まで(=以下である)と考えるのが正しい確率が0.483であるという意味合いです。上の例でxに1を指定すると答えも1になります。当然のことながら、表が出る確率が1以下であると考えるのは間違いなく正しいので、答えも1になるというわけです。ベータ分布の累積分布関数のグラフも示しておきましょう(図16)。
さて、ここまで、前回は基本的な離散分布としてベルヌーイ分布、そしてベルヌーイ試行を何回か行った場合の二項分布を紹介しました。また今回、連続分布としては一般的によく使われる正規分布を見た後、ベータ分布を紹介しました。ベータ分布はベイズ更新の計算が簡単にできるなどの理由でよく使われています。ちなみに、二項分布もnを大きくしていくと正規分布に近づくことが分かっています。
今回紹介した確率分布以外にもさまざまな確率分布がありますが、今回の内容を一通り追いかけておけば、他の確率分布についても理解が容易になると思います。もちろん、それらは好き勝手に使えるというわけではなく、データの性質によって、適切なモデル(確率分布)を当てはめる必要があります。
目標と解説【その6】: ベイズ統計と事前分布、事後分布
最後に、ベイズ統計で確率分布をどう扱うのか、簡単に紹介しておきましょう。大きな流れだけですが、今後の見通しが良くなると思います。気軽に読み進めてください。
さて、前々回で見た通り、ベイズの展開公式は以下のようなものでした。
ベイズ統計では、ベイズの定理を分布に拡張して、以下のような式を使います。確率を表すPが関数を表すfに変わったのと、周辺尤度の合計が積分に変わっただけで、基本的な形は同じです。
これまで、イカサマコインの表が出る確率を2/3とする、などとお話してきましたが、実際にはその確率が事前に分かっていることはまれです。そこで、取りあえず、事前分布の母数θを適当に決めておきます。例えば、ベルヌーイ分布ならpを1/2としておくわけです。1回目にコインを投げて表が出れば、pの値は少し大きくなりますね。これで事後分布が求められます。それをベイズ更新によって次の事前分布とするわけです。逆に裏が出ればpの値を少し小さくします。このようにして、ベイズ更新を繰り返しながら母数θを求めるというわけです。
と、流れだけ見ると簡単そうですが、周辺尤度の積分がかなり大変で、解析的に(数式だけで)計算できない場合が多く、手作業で計算するのはほとんど不可能です。しかし、コンピュータの能力が向上したことや、積分計算をシミュレーションによって効率よく行うアルゴリズム(マルコフ連鎖モンテカルロ法(MCMC)など)が登場したことなどにより、事前分布や事後分布のモデル、母数などをStanと呼ばれる言語で記述すれば、PythonやRなどで事後分布を計算できるようになってきました。
というわけで、ここから先はパソコンで計算できるわけですが、やはり、ある程度は仕組みについて見通しを付けておいた方がいいので、もう少しだけベイズ更新のお話を進めておきましょう。前掲の図18の式をよーく見ると気がつくと思いますが(言われないと気が付かないかもしれませんが)、周辺尤度は母数θで積分されるので、母数が消え、定数になります。これは、事後分布全体を積分したときに結果が1になるように調整するための定数と考えられます(規格化定数とも呼ばれます)。そこで、周辺尤度を定数kと置いてみましょう。
ずいぶん簡単になりましたね。さらに、kは単なる比例定数なので、ざっくりと以下のように書くこともできます。∝は「比例する」という意味の記号です。
続いて、幾つかデータが得られたものとすると、以下のようにベイズ更新が行われます。
Πは全ての積を表す記号でしたね。ここまでは頑張れば何とか計算できそうですが、ここに表していない規格化定数(kに当たる値)を求めるのはちょっと無理です。そこで、Stanを使って事後分布を求めた簡単な例を示すこととします。ここでは、Stanの詳しい説明はできませんが、結果だけでも見ておこうというわけです。以下の例は、Pythonで利用できるとPyStanライブラリを利用し、事後分布が正規分布に従うものとして、幾つかのデータ(20年分の選抜高校野球決勝戦の合計得点)から平均値と標準偏差を推定したものです。
結果の表を見ると(※実行のたびに表内の各数値は異なります)、mu_xの[mean]の値が10.08となっています。これは平均値の点推定値です。また、[2.5%]の値が7.51、[97.5%]の値が12.68となっています。このことから97.5%−2.5%=95%の確率で、平均値は7.51〜12.68の間にある(95%確信区間)ということを表します。選抜高校野球の決勝戦の平均得点はだいたいこの範囲にあるというわけです。sigma_xで表されている標準偏差についても同様で、点推定値が5.58、95%確信区間が4.02〜7.84となります。ちなみに、通常の方法で求めた平均値は10.00、標準偏差は5.31です。
次回は……
今回で「AI・機械学習の数学入門」のお話はひとまずおしまいです。とはいえ、大きな流れを見てきただけなので、触れるべきトピックがまだまだ残っています(例えば、対数や線形代数の詳細、今回詳しく説明しなかった「積分」など)。今後は、不定期にはなるかと思いますが、そういったトピックを拾っていこうと思っています。
Copyright© Digital Advantage Corp. All Rights Reserved.