検索
連載

Pythonの「TA-Lib」ライブラリでテクニカル指標の計算と可視化をしてみよう：「Python」×「株価データ」で学ぶデータ分析のいろは（3）（2/2 ページ）

日々変動する株価データを題材にPythonにおけるデータ分析のいろはを学んでいく本連載。第3回は複数のテクニカル指標の計算と可視化を説明します。

Share
Tweet
LINE
Hatena
前のページへ | 　　　　　　

相場の強弱に注目した分析

　売買シグナルの他に、相場の強弱に注目したテクニカル指標で株価を分析してみましょう。相場の強弱の観点から、株価の転換点を分析してみます。

RSIを利用する

　相場の強弱に注目したテクニカル指標の一つが「RSI」（Relative Strength Index）です。直訳すると相対力指数です。RSIは、一定の日数で、相場の強弱という売られ過ぎ／買われ過ぎという判断を0〜100の数値で表します。

　例えば、株価の上昇が続き、そろそろ売られるのではないか（買われ過ぎ）という時期が近づくと、RSIの値は100に近くなります。逆に、株価の下落が続き、そろそろ上がるのではないか（売られ過ぎ）という時期が近づくと、RSIの値は0に近くなります。

RSIの計算と可視化

　MACDと同様に、RSIもTA-Libで計算できます。RSIの計算と可視化をしてみましょう。

rsi14 = ta.RSI(close, timeperiod=14)
rsi28 = ta.RSI(close, timeperiod=28)
df['rsi14'], df['rsi28'] = rsi14, rsi28
mdf = df.tail(100)
apd  = [
    mpf.make_addplot(mdf['rsi14'], panel=2, color='red'),
    mpf.make_addplot(mdf['rsi28'], panel=2, color='blue')
]
mpf.plot(mdf, type='candle', volume=True, addplot=apd)
RSIの計算と可視化（Ch3.ipynb抜粋）

　RSIは、TA-LibのRSIメソッドに、終値のシリーズと日数を渡すことで得られます。1つの期間よりも、短期と長期の2つの期間で見ることが多い印象です。RSIを計算する書式は次の通りです。

％RSI％ = ％TA-Libオブジェクト％.RSI(％終値のシリーズ％, timeperiod=日数)
RSIを計算する書式

　RSIを考案したJ.W.ワイルダー氏によると、標準的な期間は14日とされています。ここでは、短期として14日、長期はその倍の28日を用いています。

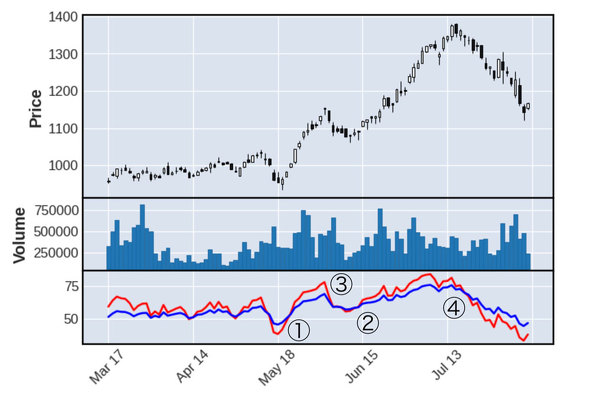
RSIの可視化
RSIの可視化

　一般的には、RSIの数値が70％以上になると買われ過ぎ、逆に30%以下になると売られ過ぎとされています。グラフを確認してみるとこの辺りに転換点があると思われます。

　またMACDの時と同様に、短期線が長期線より上がると株価が上昇（①、②）、短期線が長期線より下がると株価が下落（③、④）しています。従って①、②が買い、③、④が売りのタイミングと判断できます。

移動平均線の表示

　連載第2回で表示した移動平均線は、mplfinanceによる表示だったため、指定した日数に満たない線が表示できていませんでした。今回はTA-Libで移動平均を算出し、過不足なく移動平均線を表示してみます。

移動平均線の計算と表示

　TA-Libを使って移動平均を計算してグラフに表示してみます。テクニカル指数と同様に、TA-Libのメソッドを利用して移動平均を計算します。

ma5, ma25, ma75  = ta.SMA(close, timeperiod=5), ta.SMA(close, timeperiod=25), ta.SMA(close, timeperiod=75)
df['ma5'], df['ma25'], df['ma75'] = ma5, ma25, ma75
mdf = df.tail(200)
apd  = [
    mpf.make_addplot(mdf['ma5'], panel=0, color='blue'),
    mpf.make_addplot(mdf['ma25'], panel=0, color='purple'),
    mpf.make_addplot(mdf['ma75'], panel=0, color='yellow'),
]
mpf.plot(mdf, type='candle', volume=True, addplot=apd)
移動平均線の計算と可視化（Ch3.ipynb抜粋）

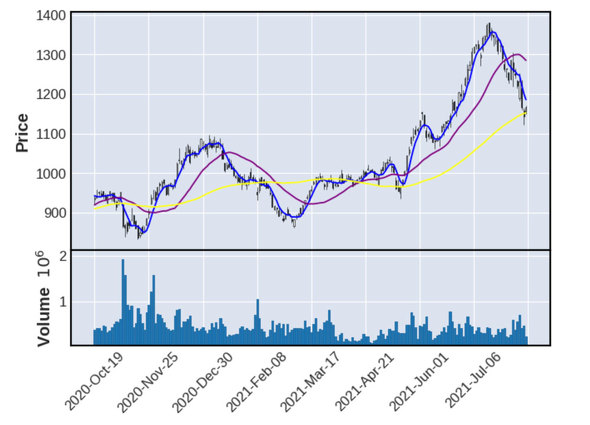
　前回と同じく5日、25日、75日の移動平均を計算して表示しています。株価データの全期間で移動平均を計算して、直近の200日のデータを表示しています。

　移動平均を計算する書式は次の通りです。

％移動平均％ = ％TA-Libオブジェクト％.SMA(％終値のシリーズ％, timeperiod=日数)
移動平均を計算する書式

　計算した移動平均はローソク足と同じ領域に表示させるため、panelプロパティの値は0にしています。

移動平均の可視化
移動平均の可視化

　グラフの期間外から計算しているので、途切れて表示することはありません。

移動平均線とMACD、RSIを表示する

　これまでに計算した移動平均、MACD、RSIを1つのグラフに表示してみます。MACDとRSIは、Y軸の値が異なるので領域を分けます。

+++スクリプト+++
mdf = df.tail(200)
apd  = [
    mpf.make_addplot(mdf['ma5'], panel=0, color='blue'),
    mpf.make_addplot(mdf['ma25'], panel=0, color='purple'),
    mpf.make_addplot(mdf['ma75'], panel=0, color='yellow'),
    mpf.make_addplot(mdf['macd'], panel=2, color='red'),
    mpf.make_addplot(mdf['macd_signal'], panel=2, color='blue'),
    mpf.make_addplot(mdf['rsi14'], panel=3, color='red'),
    mpf.make_addplot(mdf['rsi28'], panel=3, color='blue')
]
mpf.plot(mdf, type='candle', volume=True, addplot=apd)
ローソク足、出来高、移動平均、MACD、RSI（Ch3.ipynb抜粋）

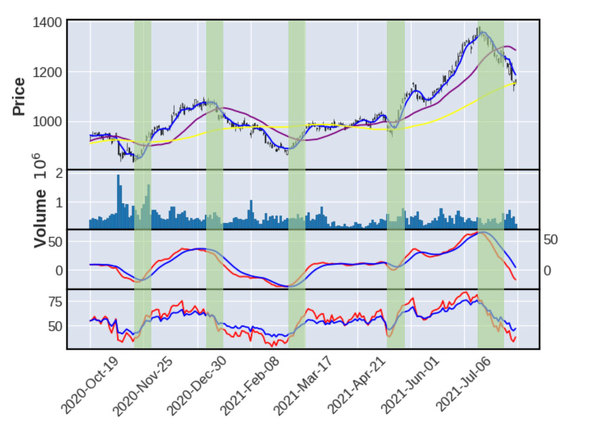
　MACDとRSIを表示する領域をpanelプロパティで分けることで、移動平均線とともに1つのグラフで表示できました。これまでのサンプルコードと同様にmake_addplotメソッドで、表示するものを定義します。

移動平均、MACD、RSIの可視化
移動平均、MACD、RSIの可視化

　移動平均線、MACD、RSIを1つのグラフで表示すると、線が重なったタイミング（緑色の帯の部分）で株価が上がる／下がるという方向性が決まると考えられます。移動平均線とは別に、テクニカル指数も可視化することで、株価の転換点と方向性をより明確にできました。

まとめ

　第2回までは、株価の推移と変動範囲を可視化しました。今回は複数のテクニカル指数を可視化するとともに、グラフから株価の転換点と方向性を見いだす（データから洞察を得る）ところまで紹介しました。

　複数のデータを利用した裏付けにより、株価の方向性を分析できたと思います。次回は、この株価の転換点に関してもう少し掘り下げて説明します。

Copyright © ITmedia, Inc. All Rights Reserved.

前のページへ | 　　　　　　
ページトップに戻る