Titanicから始めよう:特徴量エンジニアリングのまねごとをしてみた:僕たちのKaggle挑戦記
前回に引き続きEDAと特徴量エンジニアリングを行って、今回は最後にできあがったデータフレームで学習をしてみましょう。目指せ! スコアアップ!
こんにちは。Deep Insider編集部のかわさきです。冬至も過ぎて、これからはもう毎日昼間の時間が伸びて春になるのを待つばかりになりましたね。と思う冬至の翌日の朝6時です(「こんにちは」なのか「おはようございます」なのかはともかく眠いです)。
そんな人生における些細(ささい)なことはさておいて、前回は、EDA(探索的データ解析)のまねごとをしてみたところ、ディープニューラルネットワーク(DNN)に何も考えずにデータを突っ込むよりもよいスコアが出てしまったというお話をしました。今回は、その続きとなりますが、CSVからpandasのデータフレームに読み込んだデータに手を加えて、独自の特徴量を作ってみることにします。いわば特徴量エンジニアリングのまねごとをしてみようということです。
前回はデータの特性を見ながら、手作業でCSVを作成しましたが、今回は元のデータフレームを加工した結果をディープニューラルネットワークに食わせて、タイタニック号の乗客の生死を推測します。いいスコアが出るといいですねぇ(前振り)。
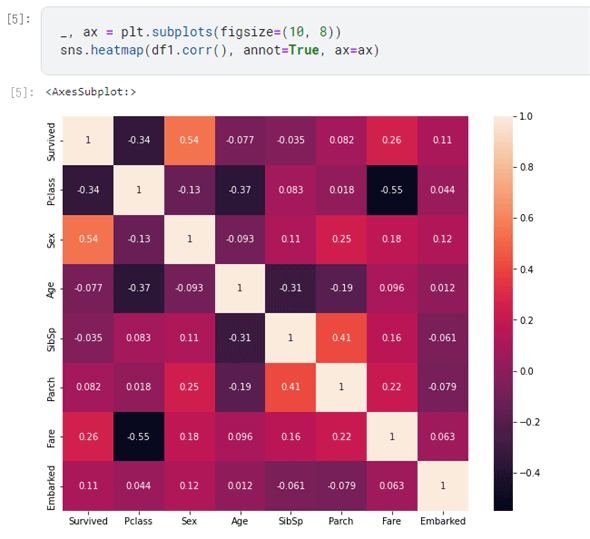
前回はEDA(のまねごと)をしたわけですが、その際に筆者自身はおおよそ次のような印象を持ちました。
- 性別(Sex)と生死の関連は強い
- チケットクラス(Pclass)と生死の関連もそれなりにありそう(高:生存←→死亡:低。ヒートマップでは負の相関として表出)
- 年齢(Age)は生死と相関がありそうと思ったけれど、ヒートマップではそれほど強く出ていない
- 旅客運賃(Fare)は生死との関連がそれなりにありそう
チケットクラスの負の相関については見落としていたのを、後から一色さんに指摘されたわけではありますが。[かわさき]
負の相関は、意外に見落としやすい注意ポイントなのかもしれませんね。[いっしき]
また前回は親族(兄弟、配偶者、子ども、親)の存在やどこで乗船したかなどの情報については取り扱っていませんでした(データフレームには情報としては含まれていましたが)。今回はこれらの情報も使って、元のデータフレームを加工していきます。
one-hotエンコーディングしてみる
Titanicコンペのデータには、乗客の性別や乗船した港などの情報が含まれています。例えば、乗船した港であれば'Q'と'S'と'C'で各港を示していますが、DNNモデルに入力できるのは数値データなので、これらを数値に変換してやる必要があります。前回は'S'を0に、'C'を1に、'Q'を2にしましたが、これらは別々の変数として表現することもできます。つまり、「Embarked_S」「Embarked_C」「Embarked_Q」という3つの変数を新たに用意し、乗船した港に応じてこれらの変数のいずれかを1にして、他は0にするという表現方法です。
1つの変数を使い「0〜2」という数値で表していたものを、3つの変数を使い「1, 0, 0」「0, 1, 0」「0, 0, 1」という数値群で表すようにするということです。このような表現にすること、あるいはそのような表現のことを「one-hotエンコーディング」と呼びます。pandasではget_dummies関数を使うことで、簡単にone-hotエンコーディングを行えます。
dftmp = pd.get_dummies(data=df0, columns=['Sex', 'Embarked'])
_, ax = plt.subplots(figsize=(10, 8))
sns.heatmap(dftmp.corr(), annot=True, ax=ax)
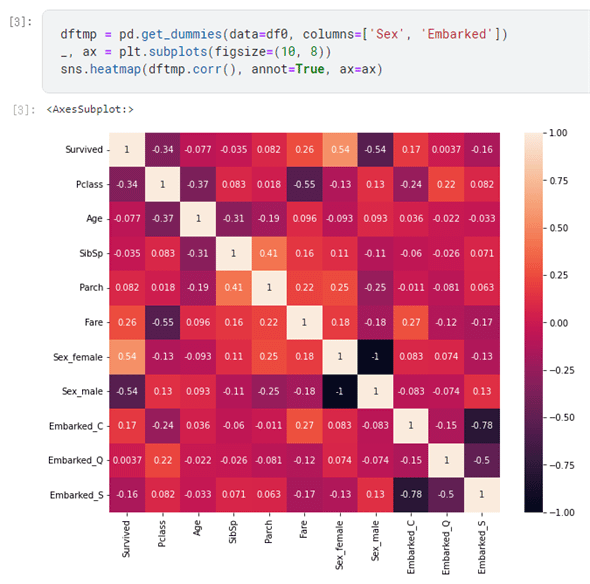
上のコードではSex列とEmbarked列の値(カテゴリ変数)をone-hotエンコーディングして、その値を含んだデータフレームのヒートマップを表示するものです。
作ってみたのはよかったのですが、よく考えたらSex_femaleとSex_maleは、どちらかが1なら、もう一方は0になるに決まっています。これは典型的な負の相関といえます(実際、上の画像ではSex_femaleとSex_maleが交差する箇所の値が-1になっていますね)。ということは、これらは一方があるだけで十分だったということです。Embarked列をone-hotエンコーディングした結果にも同様なことがいえます(つまり、3つのうちのいずれか2つが0であれば、残る1つが1となるのは分かりきっているので、2つあれば十分でしょう。実際、上の図の右下は黒くなっている、つまり負の相関が固まっているように見えます)。
また、無駄なことをしてしまった……。
そのため、実際には以下のようにget_dummies関数のdrop_firstキーワード引数にTrueを指定して、最初の要素をドロップするようにしました(コード内のdf1は訓練用のデータフレームで、dftはテスト用のデータフレームで、ここでは両方を同時に同じように加工しています)。
df1 = pd.get_dummies(data=df0, columns=['Sex', 'Embarked'], drop_first=True)
dft = pd.get_dummies(data=dft, columns=['Sex', 'Embarked'], drop_first=True)
all_df = [df1, dft]
one-hotエンコーディングは、線形回帰(重回帰分析)のときに「多重共線性」という問題を起こす可能性があるらしいから、このように生成した1要素をドロップするのは、場合によって大切みたいですね。そのための機能が用意されているget_dummies関数は便利ですね。
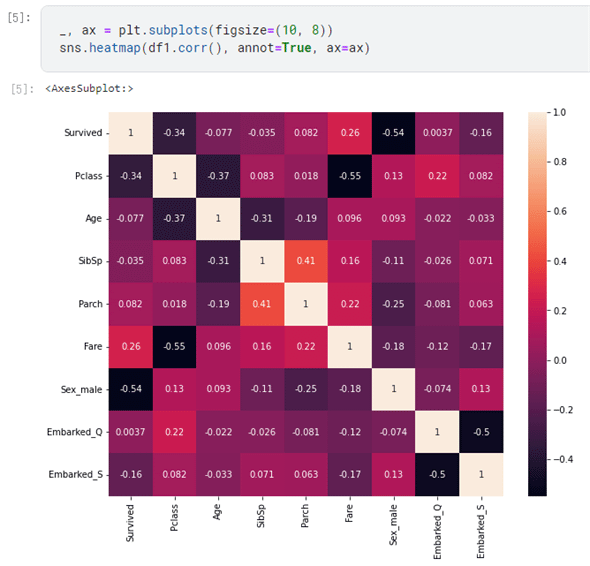
この状態でヒートマップを表示すると、以下のようになりました。
うわっ。ずいぶんと黒くなったなぁと思ったら、one-hotエンコーディングでSex列の代わりにSex_male列ができて、それが男性なら1、女性なら0となるようになったので、女性の生存率の方が高いという事実と負の相関を持つためでしょう。
Emarked_QとEmbarked_Sとの間にも負の相関があるので、これもどちらか一方があればよいのかもしれません。というか、これならone-hotエンコーディングしないで、2つの列は普通に文字列を単一数値としてエンコーディング(0/1または0/1/2で表現)するので十分だったんじゃないかと悩んだ揚げ句、単純にEmarbked_Q列も削除することにしました。
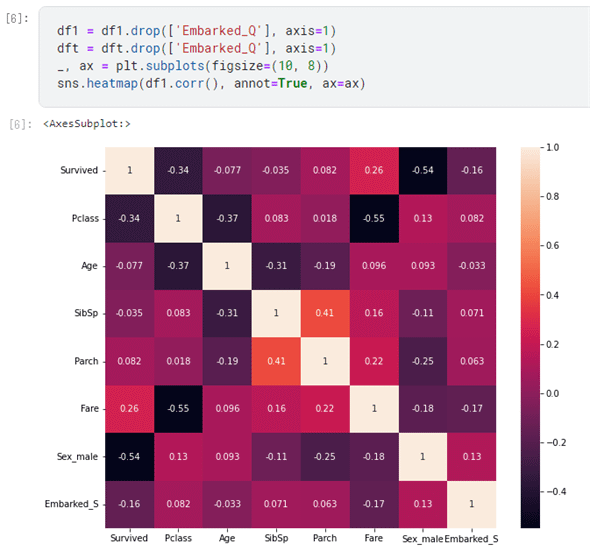
この時点でのヒートマップは次の通りです。
複数の特徴量から1つの特徴量を作ってみる
上のヒートマップの中央を見ると、SibSpとParchには相関がありそうです。前者は兄弟や配偶者の数を、後者は子どもや親の数を表しています。ここではこれらを足し合わせて、FamilySize(家族の数)という新たな特徴量を導入してみましょう(毎回同じコードを2行書くのがイヤになったので、forループを回すようにしていますね)。
all_df = [df1, dft]
for df in all_df:
df['FamilySize'] = df['SibSp'] + df['Parch']
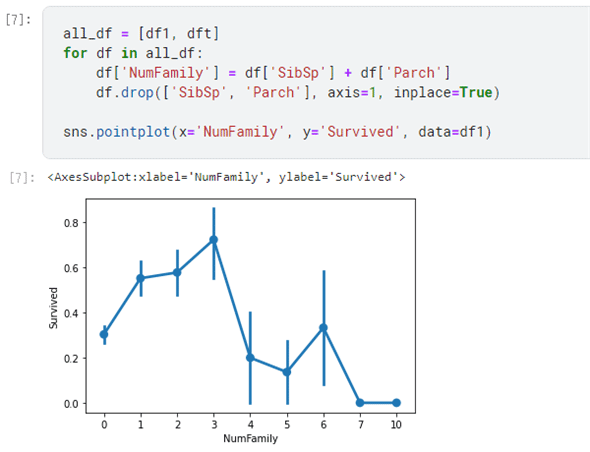
sns.pointplot(x='FamilySize', y='Survived', data=df1)
この結果は以下の通りです。
家族の数が0だと死にやすく、1〜3人は生存しやすく、それより多ければ死にやすいという傾向がありそうです。
これは面白い結果が出ましたね!(驚き)
ビニングしてみる
最後にビニングもしておきます。ビニングは前回も見ましたが、連続的な数値(ここでは年齢や旅客運賃)を離散的な値に変換して(特定の範囲に含めて)カテゴリ変数的に使えるようにするための処理です。ここでは最小値と最大値および四分位数を求めて、それらをビニングの区切りとして使うことにしました(ただし、年齢に関しては、幼児が優先して救助されたという話があるので、5歳も区切りとして含めるようにしています)。
qt_val = [0, 0.25, 0.50, 0.75, 1]
qt_age_tr = list(df1['Age'].quantile(qt_val))
qt_fare_tr = list(df1['Fare'].quantile(qt_val))
qt_age_tr.insert(1, 5)
print('Age quantile of training data:', qt_age_tr)
print('Age quantile of test data:', qt_fare_tr)
qt_age_tst = list(dft['Age'].quantile(qt_val))
qt_fare_tst = list(dft['Fare'].quantile(qt_val))
qt_age_tst.insert(1, 5)
print('Fare quantile of training data:', qt_age_tst)
print('Fare quantile of test data:', qt_fare_tst)
区切りとなる値を求めたら、以下のコードで連続的な数値をビニングで離散的な値に変換しました(ここでは欠損値は平均値で埋めるという単純な処理をしています)。
for df in all_df:
ave_age = df['Age'].mean()
df['Age'] = df['Age'].fillna(ave_age)
ave_fare = df['Fare'].mean()
df['Fare'] = df['Fare'].fillna(ave_fare)
for idx in range(len(qt_age_tr)):
df1.loc[qt_age_tr[idx] <= df1['Age'], 'Age_bin'] = idx
dft.loc[qt_age_tst[idx] <= dft['Age'], 'Age_bin'] = idx
for idx in range(len(qt_fare_tr)):
df1.loc[qt_fare_tr[idx] <= df1['Fare'], 'Fare_bin'] = idx
dft.loc[qt_fare_tst[idx] <= dft['Fare'], 'Fare_bin'] = idx
以下はデータフレームで、分割後の年齢層ごとに生存者の数を表示したものです(青線が女性、オレンジ色の線が男性、Pclassごとに表を分けています)。
普通に考えると、女性かつ若年層の生存率が高そうですが、一番左のグラフだけがそれとは異なる様相を呈しています。ちょっと気になったので、クロス集計表を作成してみました。
この表の一番左上のPclassが1、Age_binが0、Sex_maleが0(女性)に当てはまるのは1名だけで残念ながら亡くなっています。このために上のグラフではここだけが低い値となっていたわけですね。
最後にAge列とFare列を削除したデータフレームでヒートマップを作成したものが以下です。
最初から残っているのはPclass列だけとなりました(Survived列は教師データなので残っていて当然なので)。それ以外は何らかの形で加工されたものです。このデータを使って学習をするとどうなるでしょう。少しはスコアが上がってくれていればよいのですが……。
スコアが上がってくれないと切なくなりますねぇ。
特徴量エンジニアリングの結果
上記のデータフレームを使って、前々回と前回でユーティリティースクリプトとして作成(修正)したコードを使って学習を行いました。これらのコードとしては、Titanicコンペのデータセットを読み込んでPyTorchのデータセットとして扱うためのクラス、K-fold交差検証用にデータセットを訓練データと検証データに分割する関数、PyTorchで定義した線形回帰モデル/3層の全結合型DNNモデル/4層の全結合型DNNモデル、学習や評価、推測を行う関数があります。実際のコードは「kdfolds.py」と「titanic_nn.py」の2つのファイルに記述されているので、興味のある方はそちらもご覧ください。
学習を行うコードは省略します。こちらのノートブックを参照してください。K-fold交差検証で線形回帰モデル/3層の全結合型DNNモデル/4層の全結合型DNNモデルを使って、それぞれ学習ならびに推測を行うようにしています。
どうやら前回、EDAで特性を把握しながら、手作業で作成したsubmissionのスコアは0.77990だったようです。前回にどのようにして0.77990というスコアが出たかというと、単に「女性は全員生存→男性で旅客運賃が高い人は生存(そんな人はいなかった)→男性でチケットクラスが1、かつ若年層か高齢層の人は生存(1人だけ)→女性でチケットクラスが3、かつ乗船した港が'S'は死亡」という形で生死を推測したものです。
これに対して、今回は上で見たような手順でデータフレームを加工し、得られたデータフレームを使って上記の3つのモデルに学習をさせ、その後、それらにテスト用のデータを入力するという形で推測結果を得ています。これにより、乗客ごとに生死の推測結果が3つ得られます。3つの0/1があるので、最終的な予測は0と1の多い方に多数決(voting)で決定されます(このやり方は前々回と同様です)。
……
それでは結果を発表します! ジャジャジャジャジャジャジャ……ジャーーーン(長い)。結果は0.77033! 前回の結果に負けました! うへーー。とはいえ、同様な方法で推測を行った前々回のスコア「0.76794」よりはよくなっています(EDAと特徴量エンジニアリングのおかげです)。
……ままならないものですね。
ここで少し興味が湧いたので多数決をする前の3つのモデルによる推測結果もサブミットして、それらのスコアを調べてみました。
- 線形回帰モデル:0.75837
- 3層の全結合型DNN:0.73444
- 4層の全結合型DNN:0.76315
いずれの推測結果も多数決した後のスコアである0.77033よりも低いものとなりました。1つ1つの推測結果はそれほどよくないけれども、それらをアンサンブルさせることでよりよい結果が得られたといえます。これはまさに「3人寄れば文殊の知恵」みたいなものですかね。取りあえず、次回はもう少し何とかよいスコアを目指してみることにしましょう。
全てのコードを書き終えたから原稿に移ったはずが、原稿を書きながら、コードもガンガンに修正していたんですが、全体として前回のコードにはかなわなかったです……。とはいえ、前処理が重要というのは実感できました。なお、このストーリーに沿った形で当初記述していたコードではアンサンブル前の3つの推測結果の中に「0.78229」というこれまでで最高のスコアが出ていたことをお知らせします(笑)。原稿を書きながらコードを修正して、その結果、スコア、落としているじゃん(泣)。
Copyright© Digital Advantage Corp. All Rights Reserved.