［数学×Python］再帰呼び出しをマスターしよう：数学×Pythonプログラミング入門（1/4 ページ）

再帰に対して多くの人が持つであろう苦手意識を払拭（ふっしょく）するために、再帰の基本から、その考え方とプログラミングの方法を見ていく。動的計画法を利用した最小コストの計算法などについても紹介する。

[羽山博，著]

連載目次

　前回は、積分の数値計算法を見ました。今回は、「計算」から少し趣を変えて、再帰呼び出し（以下、必要がなければ「再帰」と略記します）のPythonプログラミングを見ていきます。

　再帰とは関数の定義の中でその関数を呼び出すプログラミングの方法です。自分自身を呼び出すようなイメージなので「訳が分からない」と再帰に苦手意識を持つ人も多いようですが、基本は高校で学んだ「漸化式（ぜんかしき）」をそのままコードとして表すだけです。漸化式も名前はいかめしいですが、要するに「芋づる式」に、順に値を求めていくことです。今回は、漸化式と再帰の基本的な考え方を押さえた後、応用例として、メモ化により計算量を減らす方法や動的計画法により最小コストを求める方法を見ていきます。

　Pythonの文法事項としては、関数内関数を紹介し、練習問題で辞書型データを取り扱います。ちょっと盛りだくさんですが、のんびりと読み進めてください。

　今回の練習問題としては、出発点から到達点までの経路の数を求めるプログラムと、最短経路の距離を求めるプログラムを取り上げます。

　再帰というと、プログラミングだけに登場する独特な手法だと思われるかもしれませんが、先ほども述べた通り、実は、高校数学で学ぶ「漸化式」と同じ考え方です。高校数学では、漸化式を解いて一般項を求めることや数学的帰納法による証明が学習の中心となりますが、プログラミングでは、漸化式を立てることさえできれば、自分で一般項を求める必要はありません。漸化式をそのままコードとして表現すれば答えが求められるのです。というわけで、簡単な例を使って、漸化式がどのようなものか、それをコードとして表すとどうなるのか、といったところからから見ていきましょう。

連載：

『数学×Pythonプログラミング入門 ― 中学・高校数学で学ぶ』

この連載では、中学や高校で学んだ数学を題材にして、Pythonによるプログラミングを学びます。といっても、数学の教科書に載っている定理や公式だけに限らず、興味深い数式の例やAI／機械学習の基本となる例を取り上げながら、数学的な考え方を背景としてプログラミングを学ぶお話にしていこうと思います。

羽山博

筆者紹介： IT系ライター、大学教員（非常勤）。書道、絵画を経て、ピアノとバイオリンを独学で始めるも学習曲線は常に平坦。趣味の献血は、最近脈拍が多く98回で一旦中断。

目標1： 漸化式を立てる

　今回の最初の目標は、「元金をp円、利率をr、利息の付く回数をn、n回目の元利合計をf(n)として複利計算の漸化式を立て、再帰を使って元利合計を求める関数を書く」ということです。

　「漸化式」とはa_nの値をa_n−1から求める式のことで、最初の項の値が決まれば、それ以降の項の値が次々と求められるというものです。数学の教科書にはa_n＋1の値をa_nから求めると表されているかもしれませんが、同じことですね。

　一方、「再帰呼び出し（recursive call）」とはプログラミングの方法の一つで、関数の定義の中でその関数自身を呼び出すようなものを表します。いずれも言葉だけで実感を持って理解するのはなかなか難しいので、具体的に見ていきます。「すぐに使える感」が欲しいという方に向けて身近なお金の話で考えてみましょう*1。

*1　再帰のプログラミングというと、フィボナッチの数列やパスカルの三角形などの例がよく使われますが、ちょっと浮世離れしていて、実用とはかけ離れていると感じる人もいるかもしれません。しかし、日常の中で、それらと同じ考え方で表現できる例はたくさんあります。後でそういった例も紹介します。

　例えば、1万円の元金を年利1％の利率で5年間の定期預金にしたものとします。このとき、5年後の満期時にはいくら受け取れるでしょうか。なお、一般的には半年に1回利息が付きますが、話を簡単にするために1年に1回利息が付くものとします*2。

*2　半年に1回利息が付く場合なら、利率を年利の半分の0.5％とし、利息が付く回数を10回とすれば元利合計が計算できます。なお、執筆時点では預金の利率はかなり低く、多くの銀行で0.002％程度です。これについても話を簡単にするために1％としています。

　定期預金やローンで使われる複利計算では、元金＋利息が次の元金となり、それに利息が付きます。いわば「利息に利息が付く」というわけです。具体的に計算してみると表1のようになります。

回	元金	利率	利息	元利合計
1	10,000	0.01	100	10,100
2	10,100	0.01	101	10,201
3	10,201	0.01	102.01	10,303.01
4	10,303.01	0.01	103.0301	10,406.0401
5	10,406.0401	0.01	104.060401	10,510.1005

表1　複利による元利合計の計算
1回目の元利合計（元金＋利息）の10,100円が2回目の元金になっていることが分かる。さらに、2回目の元利合計の10,201円が3回目の元金になっている。実際の定期預金では小数点以下は切り捨てになるが、ここでは小数点以下も求めた。

　このように、ある計算方法で求めた値に対して、同じ計算方法で次の値が求められる場合、漸化式を立てることができ、再帰を使ったコードが書けます。

　そこで、あらためて今回の目標です。元金をp円、利率をr、利息の付く回数をn、n回目の元利合計をf(n)として複利計算の漸化式を立て、再帰を使ったコードを書いてみましょう。漸化式の立て方については、動画でも解説しているので、ぜひご視聴ください（今回のコードはそれほど長くないので、動画では問題の考え方を中心に解説することにします）。

動画1　複利計算の漸化式を立て、再帰でコードを書く

1. 複利計算の漸化式を立て、再帰でコードを書く

　漸化式を立てるには、まず、求めたい値について、初期値などの決まった値がいくらであるかを洗い出します。複利計算の例であれば、求めたい値はn回目の元利合計f(n)です。一方、利息が付く前の元金pは決まっています。pは0回目の元利合計と考えられるので、

• n＝0のとき、f(n)＝p

となります。次に、n回目の値をn−1回目の値から求める方法を調べます。n回目の元利合計はf(n)、n−1回目の元利合計はf(n−1)であるのは明らかですね。元利合計は、

　　元金 × (1 ＋ 利率)

で求められるので、f(n)とf(n−1)の関係は、

• n>0のとき、f(n) ＝ f(n−1) × (1 ＋ r)

と表せます。f(n)の値はf(n−1)に利息が付いた値であるというわけです。nは整数であるものとし、まとめて書くと、以下のようになります。

　これで漸化式が作成できました。この漸化式をコードとしてそのまま記述しましょう（リスト1）。関数名や変数名が1文字だとコードが読みづらくなるかもしれませんが、取りあえずそのまま書きます。p（元金）、r（利率）、n（回数）の値を与える必要があるので、それらを引数として指定することにします。

def f(p, r, n):
  if n == 0:
    return p
  else:
    return f(p, r, n-1) * (1 + r)

リスト1　再帰呼び出しにより複利計算を行う関数の定義
漸化式をそのままコードとして表しただけで再帰呼び出しを行う関数が作成できる。（1）式ではn＝0の場合とn>0の場合に分けたが、ここでは、コードの見やすさを優先することとし、nが負になる場合や整数でない場合などは考慮していない（それらの値を指定すると呼び出しが無限に行われるので、実行の途中でエラーになってしまうことに注意）。そのような場合を考慮したコードは後で掲載する。

　リスト1を、引数nに注目して見てみましょう。pとrを除外して考えると、関数f(n)の定義の中で、関数f(n-1)を呼び出していることが分かります。ちゃんと（1）式と同じ形になっていますね。

　再帰では、関数fの定義の中に関数fの呼び出しが含まれているので、不思議な感じがするかもしれません。そして、それが再帰特有の「とっつきにくさ」になっているのかもしれません。しかし、それは「あまり気にしない」のが再帰克服のコツです。「そんなムセキニンな」と思われるかもしれませんが、要するに漸化式ができれば、それをそのままコードとして表すだけでいいのです。また、厳密に数式の形で表さなくても、直前の結果から、次の結果を得る方法さえ分かればコードは書けます。

　では、実行してみましょう（リスト2）。

f(10000, 0.01, 5)
# 出力例：10510.100501

リスト2　再帰呼び出しを行い、複利計算を行った結果
元金10,000円、利率1％、利払回数5回を指定して実行してみた。表1と同じ結果が得られる。

　関数名や変数名をもう少し分かりやすくし、nの値のチェックを含め、また、結果を整数として返すようにするにはリスト3のようなコードにすればいいでしょう。

def fval(pv, rate, n):
  if not isinstance(n, int) or n < 0:
    return None  # 整数でない場合や負の数の場合は答えを返さない
  elif n == 0:
    return pv
  else:
    return int(fval(pv, rate, n-1) * (1 + rate))  # 整数化して返す

リスト3　複利計算を行う関数の定義（エラー処理なども記述）
関数名のfvalはfuture value（将来価値）、引数名のpvはpresent value（現在価値）、rateは利率を表すものとした。isinstance関数を使えば、変数の型をチェックできる。上の例ではint（整数型）かどうかを調べている。

コラム　再帰のロジックを追いかける

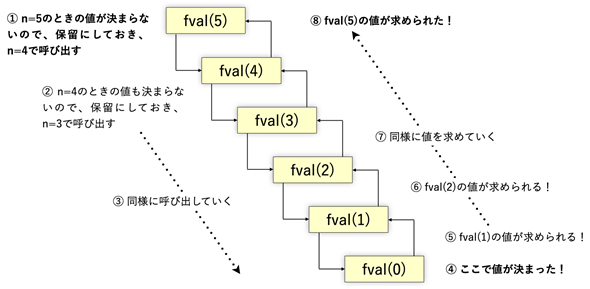
　再帰呼び出しは「n＝5の場合に関数fの値が決まらないので、取りあえず保留にしておいて、n−1、つまりn＝4で関数fを呼び出して……値が決まったら戻ってくる」というようにロジックを追いかけても理解できるのですが、逆にそれが「とっつきにくさ」のもう一つの原因になっているような気もします。これについても、漸化式をそのまま表すだけでいい（それが再帰のいいところなので）、ロジックを深追いせず「気にしない」のが得策です。しかし、中身が見えないとモヤモヤするという方もいるでしょうから、図解しておくことにしましょう。

図1　再帰呼び出しの流れ
他の引数や利息の計算などは省略して、再帰呼び出しの流れだけを図にした。関数を順に呼び出していき、値が決まったところから再び帰ってくるので「再帰」と呼ばれる。

　再帰呼び出しでは、どこかで値が決まるようにしておかないと、関数が無限に呼び出されることになってしまうので注意が必要です。その場合、関数の情報を保持しておくためのスタックと呼ばれる領域がオーバーフローしてしまい、エラーが表示されてしまいます。なお、スタックを消費しないようにするためには、関数の定義と、最後に呼び出すコードを関数の定義と同じ形にする「末尾再帰」と呼ばれる方法が使われますが、Pythonそのものでは末尾再帰がサポートされていないので、nの値があまりに大きいとエラーになることがあります。