やさしいデータ分析【確率分布編】 新連載開始!:やさしい確率分布
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編です。第1回は出発点として、推測統計の基礎となる確率分布の意味や種類、特徴を解説します。離散型分布と連続型分布の違いや種類、確率分布を表す確率質量関数/確率密度関数と累積分布関数の意味や特徴などを見ながら連載の全体像を紹介します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載(記述統計と回帰分析編)の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば(すり抜けキケン、制限速度守ってね!)。
確率分布は難しくない 〜 推測統計の基礎を固めよう
確率分布がどう役に立つのか?
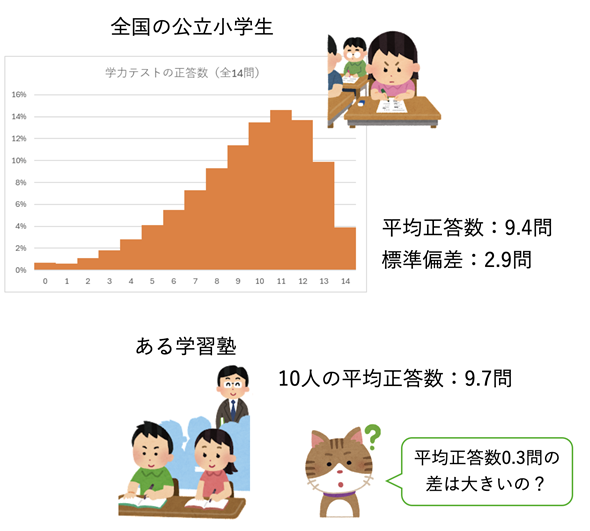
2023年度(令和5年度)に実施された文部科学省の全国学力・学習状況調査(いわゆる学力テスト)では、公立小学校6年生の国語の平均正答数は9.4問(14問中)、標準偏差は2.9問でした(国立教育政策研究所の報告書による)。
さて、ある学習塾で公立小学校に通う6年生10人の生徒に同じテストを受けさせたところ、平均正答数が9.7問だったとしましょう。皆さんは、9.7−9.4=0.3の差をどのように考えるでしょうか(図1)。学習塾の経営者としては全国の平均よりも正答数が多かったと喜びたいところでしょう。しかし、この差は「たまたま」なのかもしれません。
上のような問いに対して、何らかの根拠を持って判断を下すためには推測統計の知識が必要になります。結論だけ言うと「正答数が多いとは言えない」ということになるのですが、なぜそうなるのかは今後の連載の中でお話しします(後のお楽しみということにしましょう)。
そして、その推測統計の基礎となっているのが確率分布です。この例は、公立小学校6年生全体を母集団として、その正答数が正規分布に従っている(正規分布になっている)という前提でのお話です。確率分布を知ることにより、母集団の性質を推測したり、平均値に差があるかどうかを確かめたりすることができます。
2023年度(令和5年度)は公立の小学6年生のうち94.6%の生徒が参加しているので、母集団を公立小学校の6年生全体と考えています。なお、学力テストは、機会均等/学習状況の改善などを目的とする一方で、自治体ごとに成績を公表するのは、過度に競争をあおる可能性があるなど、さまざまな問題点も指摘されています。
確率分布とは何か、ということに関してはちょっと後回しにして、まず、確率分布がデータ分析/データサイエンスにおいて、どのような位置にあるのかを紹介しておきましょう。
データ分析と確率分布の関係とは?
『やさしいデータ分析』の記述統計と回帰分析編で、最初にデータ分析とデータサイエンスの全体像を紹介しました。図2は、その際に掲載した図の右側に、確率分布などがどう関係してくるのかを描き加えたものです。それぞれの領域/分野はお互いに関係していますが、これからの連載でお話しする内容に関しては、確率分布は推測統計の基礎として密接に関係しています。
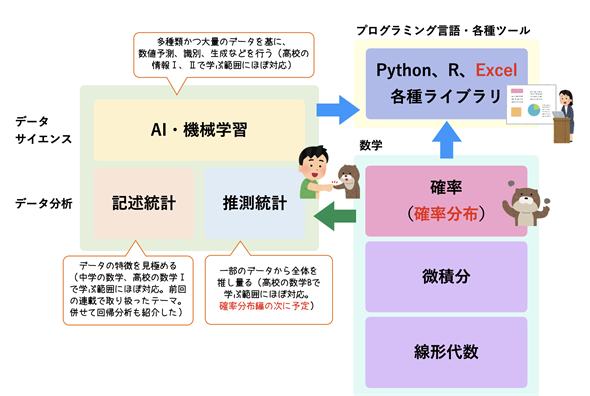
図2 データ分析/データサイエンスと数学、各種ツールの関係
数学はデータ分析やデータサイエンスの基礎となっている。とりわけ、確率分布は推測統計の基礎として極めて重要。
なお、プログラミング言語や各種ツールはデータ分析やデータサイエンスを進める上で必須となる道具で、数式や関数などのシミュレーションや可視化にも使われる。
推測統計とは、一部のデータ(標本)を基に、その元となるデータ(母集団)の性質を「推し測る」ためのさまざまな方法のことです。そのためには、確率分布の知識が必要になります。つまり、「このようなデータであれば確率的にこうなるはずだ」→「実際に得られたデータはこうだ」→「母集団はこのような分布だろう」といった推測を行うわけです。仮説検定(以下の注釈を参照)を含む推測統計は、データ分析やデータサイエンスの一つの柱となります。
図1の中の記述統計(と回帰分析)については、すでに述べたように前回の連載で解説しました。数学とプログラミングについては、数学×Pythonプログラミング入門で解説しています。また、AI・機械学習で使われる数学についてはAI・機械学習の数学入門で解説しています。その中で、確率分布についても代表的なものについて考え方や計算の方法を数学的に解説しています。
この連載では、実感を持って理解できるように、Excelを使って手を動かしながらさまざまな確率分布の形や応用例を見ていきます。なお、仮説検定とは、サンプルとして取り出したデータを基に2つのグループの平均には差があるかどうかといったことを、一定の根拠に基づいて判断する方法です。確率分布は仮説検定を行うための基礎となります。
今回は、連載の開始に当たって、確率分布を理解する上で重要となる以下のキーワードについて解説し、その後、連載の内容を紹介します。
- 離散型分布と連続型分布 …… 確率変数の取り得る値が幾つかに限られる(飛び飛びの値を取る)ものが離散型分布。確率変数が範囲内のどの値でも取れるものが連続型分布。
- 確率質量関数/確率密度関数 …… 確率分布を関数y=f(x)として表したもの。離散型分布の場合は確率質量関数と呼ばれ、連続分布の場合は確率密度関数と呼ばれる。
- 累積分布関数 ……確率質量関数の累計や確率密度関数の積分値を関数Y=F(x)として表したもの。x以下となる確率を表すもの。
これらのキーワードを初めて聞く方にとっては、いったい何を言っているのか分からないと思われるかもしれませんが、ここから少しずつ具体的に解説していきます。
そもそも確率分布って何?
では、始めます。「そもそも」のところからスタートです。そもそも確率分布とは、いったい何なのでしょうか。
「確率」に関しては、中学や高校の数学でも登場したので、基本的な意味についてはご存じだと思います。全ての事象(出来事)の中で、ある事象が起こる割合のことですね。例えば、どの目も同じように出る6面体のサイコロ(以下、単に「サイコロ」と呼びます)であれば、1の目が出る確率は1/6(6分の1)です。全体の事象が6通りあって、1の目が出るという事象は1通りですから、1/6だというわけですね。、
一方の「分布」とは、どの値がどの位置にどれぐらいあるかということです。
ということは、確率分布とは、どの確率がどの位置にどれぐらいあるかということですね。サイコロの目であれば、どの目が出る確率も1/6なので、それぞれの目が出る確率分布は図3のように表されます。
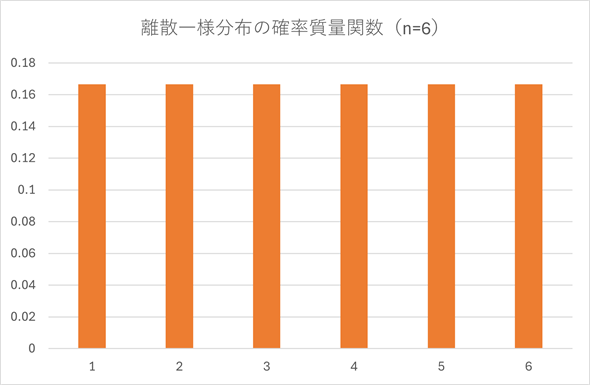
図3 サイコロの目の確率分布(離散一様分布の例)
サイコロのそれぞれの目は1/6=0.166...の確率で出るので、グラフにするとこのようになる。横軸がそれぞれの目、縦軸が確率となる。横軸の値を表す変数は確率変数と呼ばれる。グラフのタイトルにある確率質量関数の意味は後述する。
ここで重要なことは、図3が、実際にサイコロを振って出た目の数を基に求めたものではなく、理論的にはこうなるはずだ、ということです。確率分布とは、そのような理論的な分布のことです。記述統計で扱った度数分布表などの「分布」は実際に得られたデータの分布でした。この違いを意識しておいてください。
もう1つ、気が付くことがあるのではないかと思います。確率分布の全ての値の合計は1となっているということです。全事象の確率が1(=100%)となるので当然のことですが、このことも重要です。
図3の分布は、どの事象の確率も同じですね。このような確率分布を一様分布と呼びます。また、横軸(確率変数)の値が1、2、3、4、5、6と飛び飛びになっています。そのような確率分布を離散型確率分布または離散確率分布と呼びます。従って、図2の分布は離散一様分布と呼ばれます。
離散型確率分布と連続型確率分布
もう1つ、離散型確率分布の例を見ておきましょう。先ほどのサイコロを5回振ったときに1の目が何回か出る確率分布は図4のようになります。ここでは、理屈は抜きにして結果だけを紹介します。1の目が0回しか出ない、1回出る、2回出る、3回出る、4回出る、5回出るという6つの場合があります。横軸(確率変数)が図2とは異なることに注意してください。
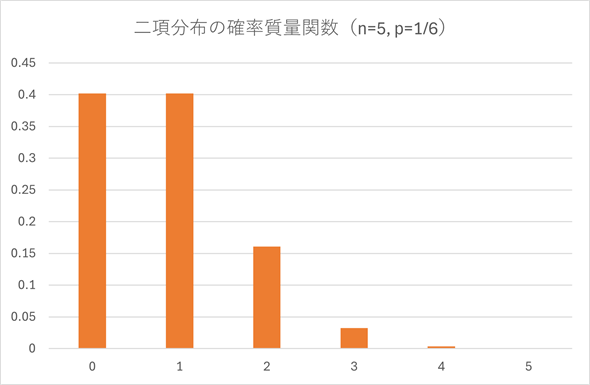
図4 サイコロを5回振って、1の目が何回か出る確率(二項分布の例)
1の目が出ない(0回出る)場合と1回出る確率がいずれも0.4程度。一方、1の目が5回とも出る確率は0.0001程度(グラフではほとんど見えない)。
図4のような分布は、二項分布と呼ばれるものです。二項分布(やその他の分布)がどのようなものかは、この連載で少しずつ解説していきます。二項分布は離散分布なので、いちいち離散二項分布と呼ばずに、単に二項分布と呼びます。
ところで、横軸の値が飛び飛びでない(範囲内のどの値でも取れるような)場合もありそうですね。そのような分布を連続型確率分布または連続確率分布と呼びます。図3で見た一様分布には、連続一様分布もあります。連続型確率分布として最も有名なものは正規分布です。今のところはやはり理屈抜きで、分布の形だけを確認しておきましょう(図5)。
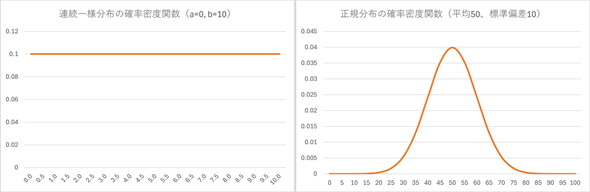
図5 連続一様分布と正規分布
連続型確率分布の場合、値が飛び飛びではないので棒グラフではなくスムーズな曲線で表される。左の例は、0〜10の範囲の連続一様分布。目盛は0.5刻みで表示してあるが、確率変数の値xは0〜10の範囲のどの値を取ることもでき、どの値も同じ確率で現れる(理想的な一様乱数のようなもの)。右の例は、平均が50、標準偏差が10の正規分布の例。正規分布はさまざまな場面で登場する。
離散型確率分布の場合、確率変数の値xに対するyの値はその事象が起こる確率です。しかし、連続型確率分布の場合、確率変数の値xに対するyの値はその事象が起こる確率ではないことに注意が必要です(後述する累積分布関数の微分係数であると考えられます)。例えば、図5の正規分布のグラフではx=50のとき、y=0.3989ですが、x=50である確率が0.3989であるというわけではありません。
確率質量関数/確率密度関数と累積分布関数
図4や図5を見ると、横軸の値をx、縦軸の値をyとしたとき、yはxの関数になっていることが分かります。つまり、xに値(例えば1など)を入れると、それに対応するyの値が自動的に決まるわけです。このような関数を、離散型分布の場合は確率質量関数と呼び、連続型分布の場合は確率密度関数と呼びます。
関数である……ということは、数式で表せますね。一応、以下に記しておきますが、今のところはあまり気にしなくてもけっこうです。今後の連載の中で分かりやすく解説します(二項分布では、xの代わりにkという文字を使っています)。
二項分布の確率質量関数
n:試行の回数、p:事象が起こる確率、k:事象が起こる回数
正規分布の確率密度関数
π:円周率、σ:標準偏差、σ2:分散、e:自然対数の底、μ:平均
また、x以下の確率を表す関数のことを累積分布関数と呼びます。離散型確率分布の場合、累積分布関数は、xに対する確率質量関数の累計値を関数として表したものです。サイコロの例であれば、k=2以下の累積分布関数の値は、k=0〜2の確率質量関数の値を全て累積した値になります(図6)。
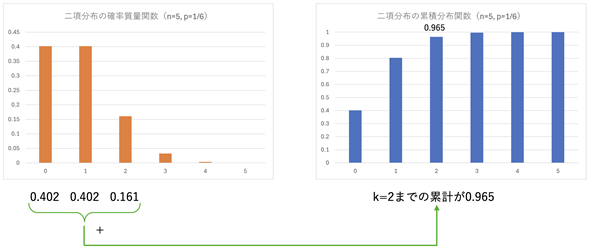
図6 二項分布の確率質量関数と累積分布関数
離散型確率分布の場合、累積分布関数の値はそれまでの値の累計となる。この例の二項分布であれば、例えば、k=2に対する累積分布関数の値はそれまでの累計、つまり0.402+0.402+0.161=0.965となる。当然のことながら、一番右の棒の高さは全ての確率を足した値なので1になる。
連続型確率分布の場合、累積分布関数は確率密度関数を積分した値を関数として表したものになります。例えば、平均50、標準偏差10の正規分布であれば、x=60以下の累積分布関数の値は、確率密度関数を−∞〜60まで積分した値になります(図7の左側、グレーの部分の面積)。x=−∞〜∞について、積分値(面積)を求め、プロットしていくと累積分布関数のグラフ(図7の右側)になります。ただし、図7ではx=0〜100の部分だけを表示してあります。
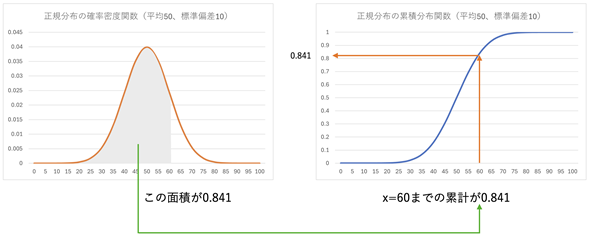
図7 正規分布の確率密度関数と累積分布関数
連続型確率分布の場合、累積分布関数の値はそれまでの積分値となる。正規分布では定義域(xの取り得る値の範囲=「台」とも呼ばれる)が−∞〜∞までとなるので、この例の場合、x=60に対する累積分布関数の値は確率密度関数を−∞〜60まで積分した値、つまり図7のグレーの部分の面積となる。累積分布関数の右端のyの値は限りなく1に近づく。
ところで、二項分布では、nの値とpの値が決まれば、確率質量関数や累積分布関数が一意に決まります。同様に、正規分布では平均μと標準偏差σが決まれば確率密度関数や累積分布関数が一意に決まります。このように、関数を一意に決める値のことを母数またはパラメーターと呼びます。
推測統計では、累積分布関数の値(累積確率)やその逆関数の値が重要となります。累積分布関数の逆関数とは、累積確率から、それに対するxの値を求める関数ということです。例えば、図7に示した正規分布の例であれば、累積確率が0.9となるxの値は62.816です。縦軸の0.9の値から逆に横軸のxの値を求めればいいというわけです。
確率分布早わかり 〜 この連載で取り扱う内容
というわけで、この連載では、さまざまな確率分布について、その意味や利用例などを、Excelを使って手を動かしながら学んでいきます。表1は次回以降少しずつ見ていく内容なので、現時点では右側の説明は気にせず、この連載でどのような分布を取り扱うのかをざっと眺めておいていただくだけで構いません。
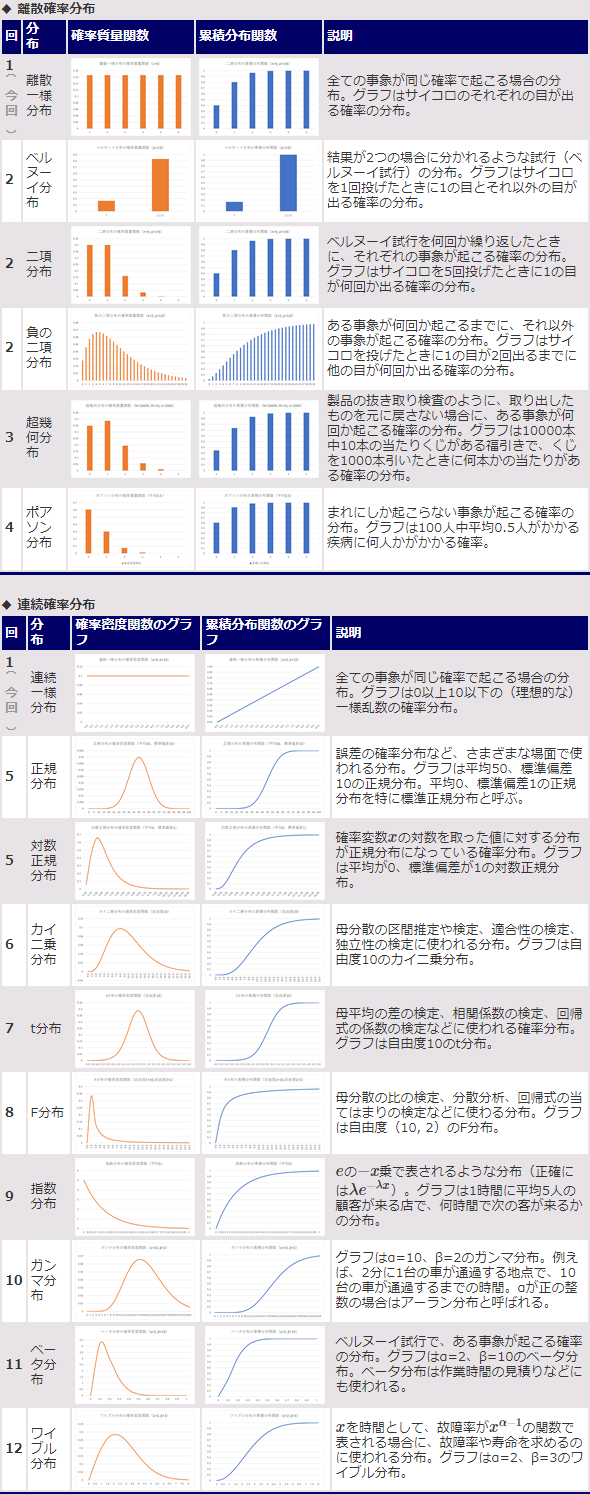
表1 連載の内容
おおむね、この表の流れに沿って、さまざまな分布について詳しく説明していく。ただし、離散一様分布と連続一様分布については簡単なので、今回の説明のみとする。表には確率質量関数/確率密度関数、累積分布関数のグラフも併せて掲載したが、パラメーターが変わると異なる形になることがある。今の段階では、だいたいの雰囲気を捉えるだけで十分。
繰り返しになりますが、確率分布は区間推定や検定などの推測統計の基礎となる考え方です。一歩ずつ着実に進めていけるように、やさしく説明するつもりです。次回からの連載にぜひご期待ください。
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.