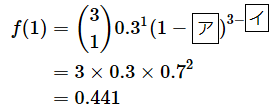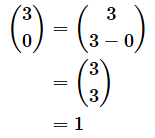[データ分析]二項分布とベルヌーイ分布 〜 離散型確率分布の基本:やさしい確率分布
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(確率分布編)の第2回。推測統計の基礎となる確率分布のうち、離散型確率分布で代表的なベルヌーイ分布と二項分布の意味や特徴などを解説します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載(記述統計と回帰分析編)の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば(すり抜けキケン、制限速度守ってね!)。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第2回です。前回は出発点として、推測統計の基礎となる確率分布の意味や種類、特徴を解説しました。今回はベルヌーイ分布と二項分布を取り上げ、それらの意味や特徴などを見ていきます。
3割打者が3人続くと確実に点を取れるのか?
野球に興味のない方にとっては、ちょっとなじみのないお話になるかもしれませんが、最近のプロ野球では3割打者がほとんどいなくなっています。2013年は15人(セ・リーグ5人、パ・リーグ10人)だったのが、2023年はたったの5人(セ・リーグ3人、パ・リーグ2人)でした。これは、投手の技術が向上したことなどが原因だと言われています。
3割打者の人数は、規定打席以上の打者について筆者が個人的に集計したものです。公式記録とは食い違っている可能性もあります。2024年の記録については、日本野球機構のページから見ることができます。
当然のことながら、ヒットが連続すれば、得点が得られる可能性が高くなります。話を簡単にするために、3人の打者がヒットを2本以上打つと得点できるものとして、3割打者が3人続くとどれぐらいの確率で得点できるかを考えてみましょう。ただし、相手の投手によって打率が変わったり、打者の調子に波があったりすることはなく、3人とも平均して3割の打率をキープしているものと考えます。
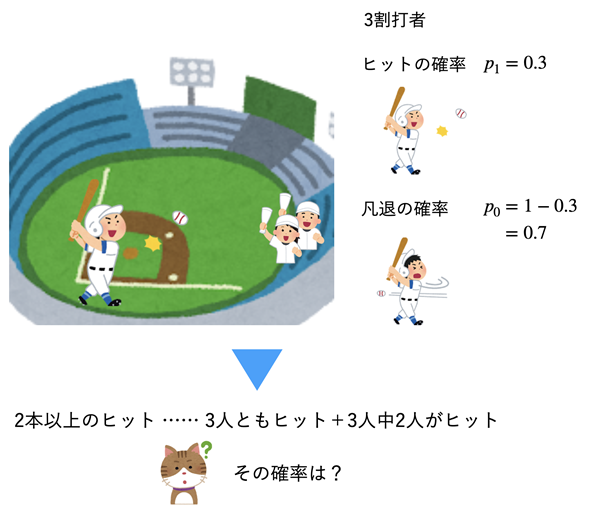
図1 3割打者が3人続いたときに、ヒットが2本以上出る確率は?
1打席でヒットを打つ確率は0.3、凡退する確率は0.7。では、3打席で2本以上ヒットを打つ確率はいくらになるだろうか。3割打者が3人続くと本当に怖いのか?
上のような問いに答えるには、ベルヌーイ分布と二項分布の知識が利用できます。まず、ベルヌーイ分布から見ていきましょう。
ベルヌーイ分布: 2種類の結果が得られる場合の確率分布
サイコロを投げたり、くじを引いたりする行為のことを試行と呼びます。厳密には、同じ条件で繰り返し行うことのできる実験や観測などのことを意味します。また、試行の結果を事象と呼びます。平たく言えば、試行とは「何かをやること」、事象とはその結果として起こる「出来事」です。
さまざまな試行のうち、1回の試行で結果が2つに分かれるものをベルヌーイ試行と呼びます。図1の例も、1回の試行が「ヒットであるか、そうでないか」の2つに分かれるので、ベルヌーイ試行です。
ベルヌーイ試行で、成功をk=1、失敗をk=0と表し、成功する確率をpと表すと、その確率分布、つまりベルヌーイ分布の確率質量関数f(k)は以下のように表されます。
3割打者の例で言えば、成功の確率は0.3、失敗の確率は1−0.3=0.7です。ちなみに、成功とは「うまくいったかどうか」という意味ではなく、「目的の事象が起こったかどうか」ということを表します。
ベルヌーイ分布は極めてシンプルな分布なので、わざわざ可視化しなくても理解できるとは思いますが、一応、Excelでグラフを描いておきます(図2)。
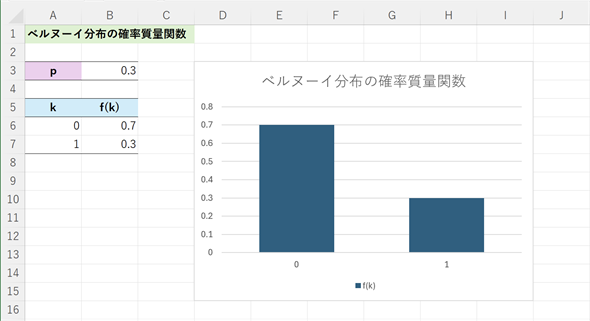
図2 ベルヌーイ分布の確率質量関数
確率変数の値kは0または1。ここでは、確率変数の値kが昇順に並ぶようにするため、kの値としてセルA6に0、セルA7に1と入力してある。従って、セルB6には=1-B3、セルB7には=B3と入力してある(上で示した(1)式とは順序が逆になっている)。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、表計算ソフトMicrosoft Excelで[ベルヌーイ分布]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。なお、Googleスプレッドシートでの操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB5〜B7を選択する
- [挿入]タブを開き、[縦棒/横棒グラフの挿入]ボタンをクリックして[集合縦棒]を選択する
- [グラフのデザイン]タブを開き、[データの選択]ボタンをクリックする
- [データソースの選択]ダイアログボックスで[横(項目)軸ラベル]の下の[編集]ボタンをクリックする
- [軸ラベル]ダイアログボックスで[軸ラベルの範囲]ボックスをクリックし、セルA6〜A7を選択する
- [OK]をクリックして[軸ラベル]ダイアログボックスを閉じる
- [OK]をクリックして[データソースの選択]ダイアログボックスを閉じる
あとは、グラフのサイズを変更したり、タイトルを設定したりして、見やすくすれば完成です(以降、これらの見た目を整えるための操作については省略します)。
二項分布: ベルヌーイ試行を何回か繰り返したときの確率分布
ベルヌーイ分布は、1回の試行の確率分布でした。野球の例で言えば、ある1人の打者について、3割の確率でヒットを打つことが分かっている場合に、ある打席でヒットを打つか凡退するかの確率分布です。今回は3人の打者についての確率を知りたいので、ベルヌーイ試行を繰り返す必要があります。そのような場合の確率分布が二項分布(Binomial distribution)です。
実は、この連載の第1回で二項分布の確率質量関数をすでに紹介しています。以下のような式でした。数式が苦手な方は目眩(めまい)を起こしそうになるかもしれませんが、今のところはあまり気にせず先に進んでください。後で具体的に解説します。また、BINOM.DIST関数を使えば簡単に答えが求められます。
n:試行の回数、p:事象が起こる確率、k:事象が起こる回数
nCkは、n個の中からk個のものを選ぶ組み合わせ数です。高校までの数学では、nCkと表しますが、一般には、
と表します。従って、(2)式は、以下のように表されます。
では、野球の例で具体的に考えてみましょう。あらかじめイメージが湧くように、最初に確率質量関数と累積分布関数のグラフを掲載しておきます(図3)。グラフの作成方法については、後で解説します。この連載の第1回でも解説しましたが、確率質量関数とは、ある確率変数に対する事象が起こる確率です。この例では、ヒットを打つ打者の人数が確率変数なので、例えば、2人の打者がヒットを打つ確率(k=2に対する確率)などが確率質量関数の値に当たります。一方の累積分布関数は、ある確率変数の値以下の事象が起こる確率の累計です。例えば、2人以下の打者がヒットを打つ確率(k=0の場合とk=1の場合とk=2の場合の累計)が累積分布関数の値に当たります。全ての場合を表とグラフにしたのが図3です。
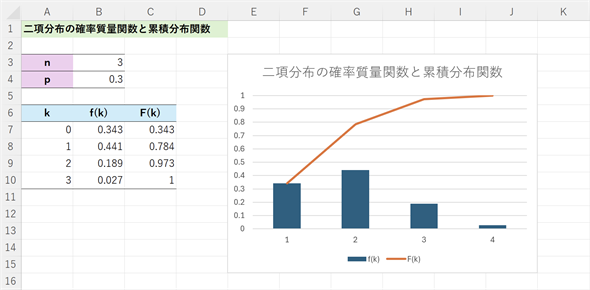
図3 3人の3割打者のうち何人かがヒットを打つ確率(確率質量関数と累積分布関数)
確率変数の値kは「ヒットを打つ人数」。f(k)が確率質量関数の値。例えば、n=3人のうち、k=0人がヒットを打つ確率f(0)は0.343。F(k)は累積分布関数の値。例えば、n=3人のうち、ヒットを打つのがk=1人以下である確率F(1)は0.784。棒グラフは確率質量関数を、折れ線グラフは累積分布関数を可視化したもの。
ここから、図3に示したf(k)の具体的な値が、(3)式でどのようにして求められるかを見ていきます。3人の打者のうち何人かがヒットを打つ確率について、全ての場合を洗い出してみましょう。
3人の3割打者が3人ともヒットを打つ確率
図3の確率変数の値kは昇順に並んでいますが、逆に、kの値の大きい方から見ていきます。つまり、3人ともヒットを打つ確率からです。これは簡単です。図4をご覧ください。

図4 3割打者が3人ともヒットを打つ確率
3人ともヒットを打つ確率は0.3×0.3×0.3=0.027。つまり、2.7%となる。3連打が出るのはかなり確率の低い事象。実際のところ、投手の調子によってはメッタ打ちにされることもあるが、あくまでも常に3割の確率でヒットが出るとした場合の話。
3人ともヒットを打つ確率は0.3×0.3×0.3=0.027です。このような場合は1通りしかありません。その、1通りというのは、3人の中から3人を選ぶ場合の数です。他に選びようがないですね。
ここで、注意すべき点は(本来は、もっと早く言っておくべきことなのですが)、それぞれの試行が独立であることが大前提になっているということです。前の打者の結果によって、次の打者の行動(ヒットの確率)が変わるとすれば、独立ではありません(そのような関係を従属と呼びます)。実際の試合では、前の打者が3塁打を打ったので次の打者は外野フライでもいいとか、強打者であっても1点を競っている場合はスクイズを試みるといったことがありますが(……といったところが野球の面白さではあるのですが)、ここでは、前の打者の結果とは関係なく、次の打者は常に3割の確率でヒットを打つものとしています。
3人の3割打者のうち2人がヒットを打つ確率
次に、2人がヒットを打つ確率を考えてみましょう。2人がヒットを打つ確率は0.3×0.3×0.7で求められます。ただし、1人目と2人目がヒット、1人目と3人目がヒット、2人目と3人目がヒットという3通りの場合があります(図5)。
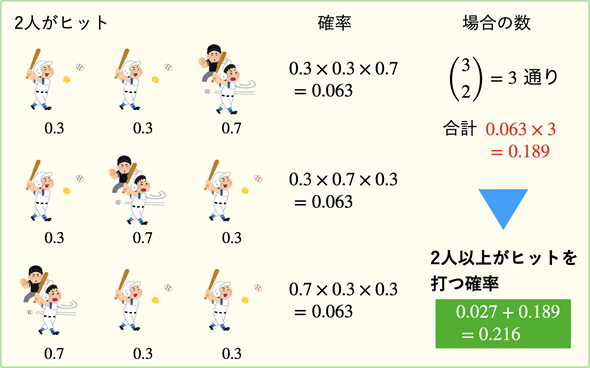
図5 3人の3割打者のうち2人がヒットを打つ確率
2人がヒットを打つのは3通りの場合があり、それぞれの確率は0.3×0.3×0.7=0.063となる(掛け算の順序が異なっているだけでいずれも0.063となる)。従って、合計すると0.063×3=0.189となる。
図4と図5から、2人以上がヒットを打つ確率は0.027+0.189=0.216となることが分かります。2割ちょっとですね。上でも述べたように実際には一筋縄にはいきませんが、3割打者が3人続いたとしても8割方は得点されないと考えれば、投手も気が楽になるのではないでしょうか。
さて、ここで、少し計算を一般化してみましょう。少しゆっくりと考えながら読んでいただきたいので、穴埋め問題形式で見ていきます。オレンジ色の部分をクリックまたはタップすると答えが表示されます。
図5の場合。成功確率をpとすると、それぞれのヒットが出る確率はp2×(1−p)1となっていることが分かります。pの指数の 2 は成功数、つまり k の値ですね。一方の(1−p)の指数の1は、試行数をnとすると、n− k の値です。nは試行数の3、 k は成功数の2なのでn− k =1ですね。ということで、それぞれの確率は、以下のように表されます。
これが3通りあったわけです。3通りというのは、3人の中からヒットを打つ2人を選ぶ場合の数です。つまり、
です。3というのは n の値、2というのは k の値なので、一般に、
と表されます。これらを掛けると、以下のようになりますね。
これは(3)式の右辺です。以下に再掲します。
組み合わせ数の求め方
(5)式の組み合わせ数の求め方も確認しておきましょう。以下の公式を使います。
!は階乗を表します。n!は、n × (n−1) × … × 1です。ただし、この公式を正直に使うよりも、以下の方法で計算するのが楽です。
n=3、k=2でやってみましょう。以下のようになりますね。穴埋め問題にしています。
答え: ア= 2 、イ= 2
なお、以下の等式が成り立ちます。
例えば、n=12個のうちからk=9個選ぶ組み合わせ数は、
で計算するよりも、
の方が簡単です。
続いて、1人しかヒットを打たない場合と、1人もヒットを打たない場合についても、確率を求めてみましょう。
3人の3割打者のうち1人がヒットを打つ確率
1人がヒットを打つ確率は0.3×0.7×0.7で求められます。ただし、1人目がヒット、2人目がヒット、3人目がヒットという3通りの場合があります(図6)。
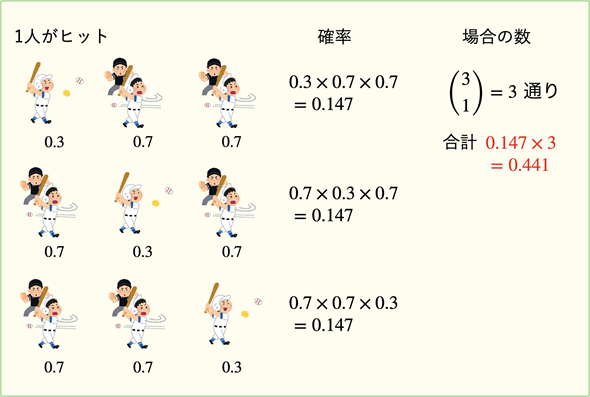
図6 3人の3割打者のうち1人がヒットを打つ確率
1人がヒットを打つのは3通りの場合があり、それぞれの確率は0.3×0.7×0.7=0.147となる(掛け算の順序が異なっているだけでいずれも0.147となる)。従って、合計すると0.147×3=0.441となる。
この例については、公式に従って計算してみましょう。
にn=3、k=1を代入すればいいですね。まず、組み合わせ数を計算しておきましょう。k=1のときは、計算するまでもなく、
なので、組み合わせ数は3です。p=0.3なので、以下のようになります。これも穴埋め問題にしています。
答え: ア= 0.3 、イ= 1
3人の3割打者のうち0人がヒットを打つ確率
3人のうち0人がヒットを打つということは、誰もヒットを打たない(全て確率は0.7)ということですね。これは簡単です(図7)。
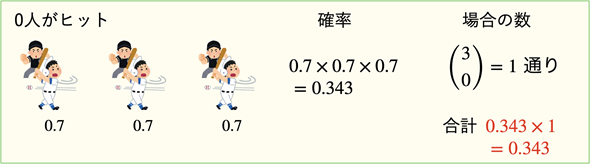
図7 3人の3割打者のうち0人がヒットを打つ確率
3人ともヒットを打たない確率は0.7×0.7×0.7=0.343。つまり、34.3%となる。3人の中から0人を選ぶ組み合わせ数は1なので(後述)、合計も0.343となる。
3人の中から0人を選ぶ組み合わせ数というのはちょっと想像しづらいですが、(8)式に当てはめると、1であることが分かります。
図4〜図7の確率を合計すると、0.027+0.189+0.441+0.343=1となることも確認しておいてください。
二項分布の確率質量関数と累積分布関数を可視化してみよう
ここまでは、具体的な例を基に、(3)の公式を理解することに重点を置いてきました。ここからは、確率質量関数や累積分布関数の値を求めたり、可視化したりする方法を見ていきます。図3のような表やグラフを作成する方法を見ていこうというわけですね。図3を再掲して、その後に手順を示すことにします(図8)。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、Excelで[二項分布]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。なお、Googleスプレッドシートでの操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB7に=BINOM.DIST(A7:A10,B3,B4,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルB7〜B10)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルC7に=BINOM.DIST(A7:A10,B3,B4,TRUE)と入力する
- スピル機能が使えない場合は、セル範囲(セルC7〜C10)を選択して関数の入力終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルB6〜C10を選択する
- [挿入]タブを開き、[複合グラフの挿入]ボタンをクリックして[集合縦棒 - 折れ線]を選択する
- [グラフのデザイン]タブを開き、[データの選択]ボタンをクリックする
- [データソースの選択]ダイアログボックスで[横(項目)軸ラベル]の下の[編集]ボタンをクリックする
- [軸ラベル]ダイアログボックスで[軸ラベルの範囲]ボックスをクリックし、セルA7〜A10を選択する
- [OK]をクリックして[軸ラベル]ダイアログボックスを閉じる
- [OK]をクリックして[データソースの選択]ダイアログボックスを閉じる
BINOM.DIST関数の引数は以下のように指定します。
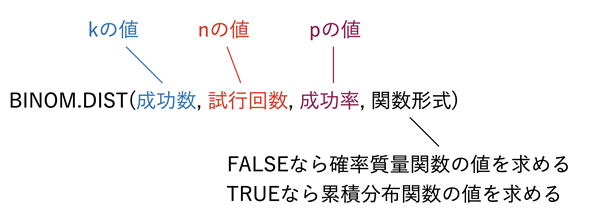
図9 BINOM.DIST関数に指定する引数
図8の例では、成功数(kに当たる値=目的の事象が起こる回数)としてA7:A10というセル範囲を指定しているので、スピル機能によりセルA7〜A10の成功数に対する確率質量関数の値や累積分布関数の値が一度に求められる。
なお、サンプルファイルには、(3)式に従って確率質量関数と累積分布関数の値を求めた例も含めてあります。興味のある方はご参照ください。
今回は、離散型確率分布の基本的な例として、ベルヌーイ分布と二項分布を取り上げました。実は、二項分布は、連続型確率分布として最もよく使われる正規分布の基礎ともなっています。また、ある打者が例えば10打数のうち4回ヒットを打ったとき、(たまたま調子が良かっただけかもしれないので)その打者は3割打者であると自信を持って言えるか、といった検定(二項検定)のためにも使われます。これらのことについても、いずれ紹介したいと思います。
さて、次回は、離散型確率分布の別の例として、超幾何分布を取り上げます。超幾何分布は、非復元抽出(引いたくじを元に戻さないような場合)の確率を求めるのに使われます。次回もお楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
二項分布の確率質量関数や累積分布関数の値を求めるための関数
BINOM.DIST関数: 二項分布の確率質量関数や累積分布関数の値を求める
形式
BINOM.DIST(成功数, 試行回数, 成功率, 関数形式)
引数
- 成功数: 目的の事象が起こる回数を指定する。
- 試行回数: 試行の総数を指定する。
- 成功率: 目的の事象が起こる確率を指定する。
- 関数形式: 以下の値を指定する。
- FALSE …… 成功数に対する確率質量関数の値を求める
- TRUE …… 成功数までの累積分布関数の値を求める
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.