連載

2025年1月24日

［pandas超入門］Diabetesデータセットを使って回帰分析してみよう（可視化編）：Pythonデータ処理入門

連載の最後にデータセットの読み込み、可視化、回帰分析などの作業を一気通貫でやってみます。今回はそのうちのデータセットの読み込みと可視化を取り上げます。

[かわさきしんじ，Deep Insider編集部] PC用表示関連情報

LINE

Hatena

連載目次

本シリーズと本連載について

　本シリーズ「Pythonデータ処理入門」は、Pythonの基礎をマスターした人を対象に以下のような、Pythonを使ってデータを処理しようというときに便利に使えるツールやライブラリ、フレームワークの使い方の基礎を説明するものです。

NumPy（「NumPy超入門」の目次はこちら）
pandas（本連載）
Matplotlib

　なお、本連載では以下のバージョンを使用しています。

Python 3.12
pandas 2.2.1

　前回は、正規化と標準化について少し詳しく見てみました。今回と次回（最終回）は連載のまとめとして、Titanicデータセットとは別のデータセットを使って、データセットの可視化（今回）と回帰分析（次回）を行う予定です。

　まずは前回と同様に以下のパッケージをインポートしておきましょう。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

pandasとNumPyのインポート

　これらに加えて、今回はscikit-learnに付属のデータセットを使用するので、以下のコードも実行しておきましょう。

from sklearn import datasets

sklearnパッケージからdatasetsモジュールをインポート

使用するデータセット

　今回はscikit-learnに付属の「Diabetes Dataset」というデータセットを使用します。これは「年齢／性別／BMI／血圧」などの特徴量と、1年後の糖尿病の進行度合いを表すラベルで構成されるデータセットです。詳しい説明は上記のリンクを参照してください。

　特徴量として用意されているのは以下の10種類です。

age：年齢
sex：性別
bmi：BMI（Body Mass Index：体重を身長の二乗で割った値で肥満度を示す）
bp：血圧（blood pressure）
s1：血液中の総コレステロール値
s2：低比重リポたんぱく質（悪玉コレステロール）
s3：高比重リボたんぱく質（善玉コレステロール）
s4：総コレステロール値／善玉コレステロール
s5：血液中の中性脂肪の対数
s6：血糖値

　また、糖尿病の1年後の進行度合いにはtargetというラベルが付けられています。

　以下ではpandasのDataFrameオブジェクトにこのデータセットを読み込んで、その概要を表示したり、それらの相関係数を計算してヒートマップをプロットしたり、相関の高そうな特徴量とラベルを散布図にプロットしたりしていきましょう。最終的にはこのデータセットを使って回帰分析を行う予定です。

データの読み込み

　Diabetesデータセットを読み込むにはsklearn.datasetsモジュールのload_diabetes関数を呼び出すだけです。上で見た特徴量はそのdata属性として、ラベルはtarget属性としてアクセスできます。以下のコードではそれらを基にDataFrameオブジェクトを作成しています。

diabetes = datasets.load_diabetes()
X = diabetes.data
y = diabetes.target
feature_names = diabetes.feature_names
df = pd.DataFrame(X, columns=feature_names)
df['target'] = y
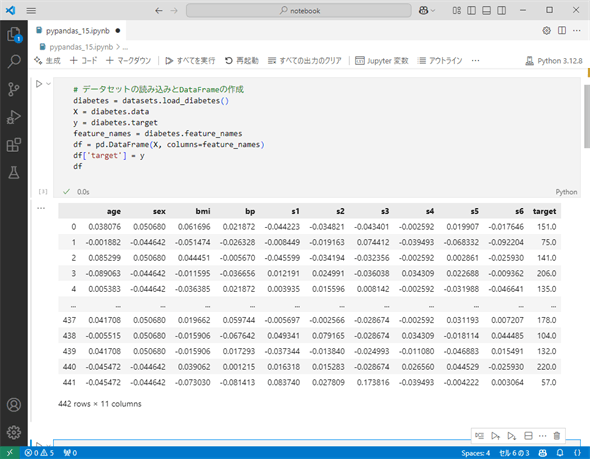
df

Diabetesデータセットの読み込みとDataFrameオブジェクトの作成

　Visual Studio Code（以下、VS Code）で上記のコードを実行した結果を以下に示します。

Diabetesデータセットを読み込んでDataFrameオブジェクトを作成したところ

　下の方にある「442 rows × 11 columns」という表示から、このデータセットは442行のデータが含まれていて、各行は11列のデータ（10列の特徴量とラベル）で構成されていることが分かります。

　では、infoメソッドを実行してみましょう。

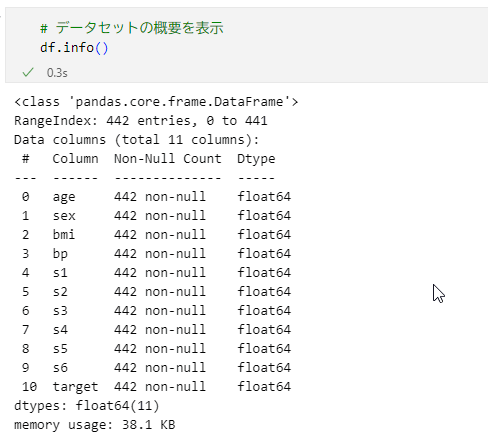
df.info()

DataFrameオブジェクトの概要を表示

　すると、次のような結果が得られます。

infoメソッドの実行結果

　この結果からは、このデータセットには欠損値がないこと、全ての行／列の値が浮動小数点数値になっていること、行数は442であること（既に上で述べていますが）、列数が11であること（こちらも）が確認できます。

　次にdescribeメソッドを呼び出してみましょう。

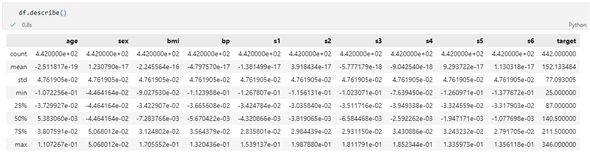
df.describe()

describeメソッドの呼び出し

　以下に実行結果を示します。

describeメソッドにより表示された基本統計情報

　describeメソッドはDataFrameオブジェクトの基本統計情報を計算して、表示するメソッドです。各列について以下を計算してくれるのでした（数値データの場合）。

count：被欠損値の数
mean：平均値
std：標準偏差
min：最小値
25％、50％、75％：四分位数
max：最大値

　上の結果を見ると、次のようなことが分かります（特徴量）。

各列とも平均値は0くらい
標準偏差が1ではない
最小値と最大値が0～1の範囲にはない

　正規化とは一般的には「データを0～1の範囲にスケールする」ことであり（Min-Max Normalize）、標準化とは同じく一般的には「データを平均0、標準偏差1となるようにスケールする」ことでした。しかし、このデータセットはそのどちらでもない形で何らかのスケーリングがなされているようです。

　実は先ほど紹介したこのデータセットについての解説ページには「平均0、ユークリッドノルム（L₂ノルム）1（＝各値の二乗を全て合計した値が1、つまりsum(x²)＝1）に正規化された値となっているので注意してほしい」と書いてあります。このことからも、スケーリングはされているけれど、前回と前々回に見た正規化と標準化とは異なる方法が採られているということです。

　というわけで、少し横道に外れますが、本当に特徴量を含む列について「sum(x²)＝1」となるかを試してみましょう。

def calc_l2norm(x):
return np.sqrt(np.sum(x ** 2))

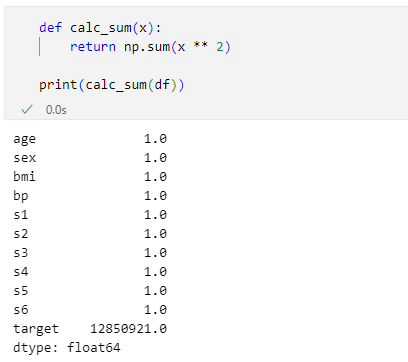
print(calc_l2norm(df))

本当にそうなるかを確認するために関数を定義

　これは各列の値を二乗した総和を計算する関数を定義して、その結果を表示するコードです。これを実行すると次のようになりました。

特徴量を含む全ての列でデータを二乗した総和が1になった！

　おお、確かに特徴量を含む列では二乗した値の総和が1になっていることが確認できました。書いてあることとはいえ、ほんとうにそうなっていることが確認できるとスッキリしますね。

　なお、ラベルについてはこのようなスケーリングがなされていないのは、ラベルの値は1つ以上の特徴量を基にその値にたどり着くための目的だからと考えればよいでしょう。多くの場合はラベルについてはこうしたスケーリングは不要です。

ヒートマップをプロットしてみよう

　次にDiabetesデータセットの各列について相関係数を計算して、そのヒートマップをプロットしてみます。といっても、これはDataFrameオブジェクトが持つcorrメソッドを呼び出すだけです。相関係数については「NumPy超入門」の「相関係数とヒートマップ、散布図を使ってデータセットをさらに可視化してみよう」でも取り上げているので、興味のある方はそちらも参照してください。

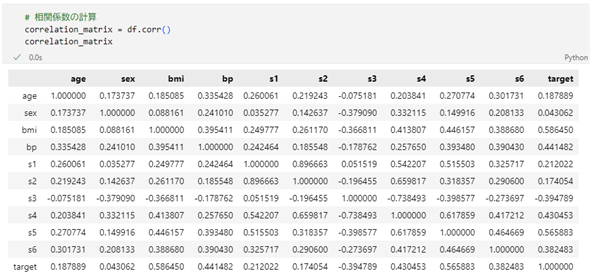
correlation_matrix = df.corr()
correlation_matrix

相関係数の計算

　実行結果を以下に示します。

相関係数

　後はこれをもっと分かりやすく視覚化するだけです。ここではMatplotlibのみを使って次のようなコードを書きました。

# ヒートマップのプロット
plt.figure(figsize=(10, 8))
plt.imshow(correlation_matrix, cmap='coolwarm')
plt.colorbar()

# 軸ラベルの設定
ticks = np.arange(len(correlation_matrix))
labels = correlation_matrix.columns
plt.xticks(ticks=ticks, labels=labels)
plt.yticks(ticks=ticks, labels=labels)

# 相関係数を各グリッドに表示
for i in range(correlation_matrix.shape[0]):
    for j in range(correlation_matrix.shape[1]):
        value = correlation_matrix.iloc[i, j]
        plt.text(j, i, f"{value:.2f}", ha="center", va="center")

plt.show()

ヒートマップのプロット

　簡単な説明をしておくと、matplotlib.pyplot.imshow関数は与えたデータを2次元の格子状のイメージとして表示するものです。ここでは作成したDataFrameオブジェクトを渡しているので、これを基にデータの可視化が行われます。cmapパラメーターには使用するカラーマップを指定します。ここでは'coolwarm'を指定していますが、この指定により、個々のグリッドに対応する元データの値が1に近ければ赤に近い色で、-1に近ければ青に近い色で背景が塗りつぶされるようになります。つまり、相関係数が高ければ赤く、低ければ青く塗られるということです。また、matplotlib.pyplot.colorbar関数を呼び出してヒートマップの隣にカラーバー（数値に対応する色を表示するバー）を加えています。

　次に軸ラベルの位置とそのラベルを指定して、matplotlib.pyplot.xticks関数とmatplotlib.pyplot.yticks関数を呼び出して軸ラベルを表示するようにしています。

　最後に相関係数を格納しているDataFrameオブジェクト（correlation_matrix）の各データをfor文で取り出して、ヒートマップの対応する箇所に書き出しています。

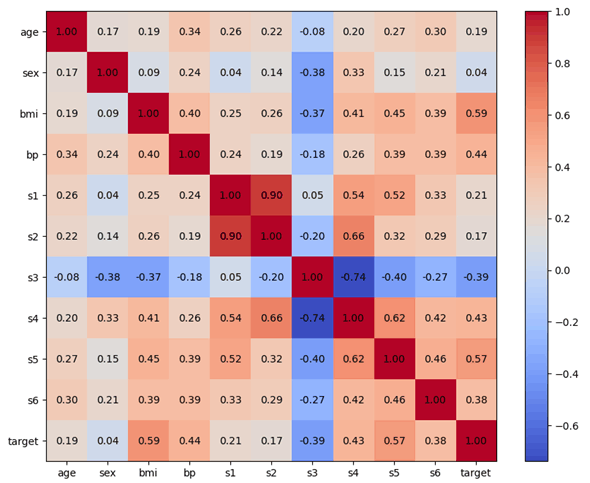
　プロットされたヒートマップを以下に示します。

ヒートマップ

　ここで見るのは取りあえず、target列と他の列との相関です。赤に近い色のものほど正の相関が強い傾向にあり、青に近い色のものほど負の相関が強い傾向にあります。相関係数が0.3より大きいもの（正の相関）と0.3より小さいもの（負の相関）にここでは注目してみましょう。以下に列挙します。

bmi（0.59）：BMI
bp（0.44）：血圧
s3（-0.39）：善玉コレステロール
s4（0.43）：総コレステロール値／善玉コレステロール
s5（0.57）：中性脂肪
s6（0.38）：血糖値

　負の相関を持つものは「善玉コレステロール」だけです。なんか聞いたことある！　ってなりました（身体によさそう）。対して正の相関を持つものはBMIや血圧、中性脂肪などです。こうやって列挙すると、肥満や高血圧が糖尿病にはよくないという定説がなるほどと思えてきますね。これらの列が回帰分析を行うモデルに使用する候補と言えます。

　そこで今度はこれらの相関について考えてみましょう。

# ラベルとの相関が強いものだけを選んでDataFrameオブジェクトを作成
cols = ['bmi', 'bp', 's3', 's4', 's5', 's6']
df2 = df[cols]
correlation_matrix_2 = df2.corr()

# ヒートマップのプロット
plt.figure(figsize=(8, 6))
plt.imshow(correlation_matrix_2, cmap='coolwarm')
plt.colorbar()

# 軸ラベルの設定
ticks = np.arange(len(correlation_matrix_2))
labels = correlation_matrix_2.columns
plt.xticks(ticks=ticks, labels=labels)
plt.yticks(ticks=ticks, labels=labels)

# 相関係数を各グリッドに表示
for i in range(correlation_matrix_2.shape[0]):
    for j in range(correlation_matrix_2.shape[1]):
        value = correlation_matrix_2.iloc[i, j]
        plt.text(j, i, f"{value:.2f}", ha="center", va="center")

plt.show()

ラベルとの相関が強い列同士の相関を見る

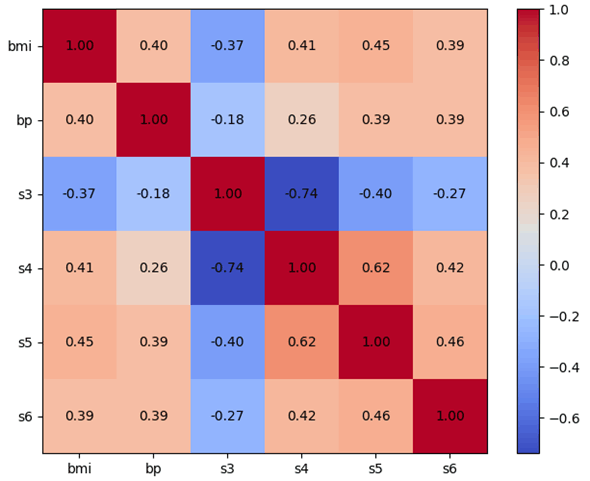
　コードは先ほどのものと同様なので、説明は省略して、実行結果だけを示します。

実行結果

　この結果を見ると、上で選んだ列の多くが互いにそれなりに強い相関関係にあることが分かります（正の相関、負の相関のいずれも）。中でもBMIは他の全ての列と強い相関関係にあり、特にs3とは-0.74と強い負の相関を持ちます（他は0.39～0.45と正の相関関係）。また、s3も他の全ての列と負の相関関係にあります（BMIを除くと-0.18～-0.44）。実際に回帰分析を行う際には、これら2つの列をモデルの特徴量として優先的に使用して、他の列については予測精度の向上を検証した上で特徴量として追加するか削除するかを検討することにしましょう。なお、今回は多重共線性についての考察は説明の目的ではないため省略します。

散布図をプロットしてみよう

　最後に上で選んだ各特徴量とラベルとの関係を散布図としてプロットしてみましょう。

cols = ['bmi', 'bp', 's3', 's4', 's5', 's6']

fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(15, 10))
axes = axes.flatten() # 1次元配列に変換

for n, col in enumerate(cols):
    ax = axes[n]
    ax.scatter(df[col], df['target'])
    ax.set_title(col)
    ax.set_xlabel(col)
    ax.set_ylabel('target')

plt.show()

散布図をプロットするコード

　このコードではmatplotlib.pyplot.subplots関数で2行3列のサブプロット領域を作成して、そこにcolsリストで指定した列の散布図をmatplotlib.axes.Axes.scatterメソッドでプロットし、散布図のタイトルと軸ラベルを設定しています。

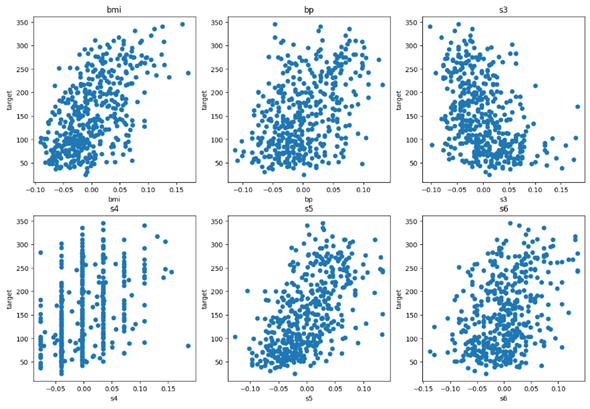
　以下は実行結果です。

散布図

　bmiは正の相関があることが分かるような散布図になっていますね。s3も負の相関があることが何となく分かります。他の列についても「何となくそんな感じかな？」程度には相関がありそうな散布図になりました。

　また、今回は取り上げませんでしたが、プロットされた散布図を見ると外れ値もデータセットの中には含まれているかもしれないなと気が付きました（これについては次回で取り上げる予定です）。

　今回はデータセットに欠損値がない、既に何らかのスケーリングが行われているなどの理由でそれらの処理を省略してしまいましたが、本来はここまでの段階で今回見たようなデータの可視化に加えて、欠損値の処理や上でも述べた外れ値に対する対処、正規化や標準化によるスケーリング、カテゴリ変数のエンコードなどを行うことで、データを機械学習やディープラーニングに投入できるようにブラッシュアップすることになります。

　次回はこのデータセットを使って回帰分析を行うコードを書き、その評価やモデルの改善などに挑戦し、本連載を終わる予定です（その中で外れ値の処理も行う予定です）。

「Pythonデータ処理入門」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう