検定に必要なサンプルサイズを、無料ツールG*Powerで簡単に求める方法：やさしい推測統計（仮説検定編）

初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ（仮説検定編）の第6回（番外編）。今回は、G*Powerという便利なツールを使い、検定に当たって必要となるサンプルサイズを簡単に求める方法を紹介します。

[羽山博，著]

連載目次

連載：

『社会人1年生から学ぶ、やさしい推測統計（仮説検定編）』

　この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計（区間推定編）」に続く「推測統計（仮説検定編）」です。
　この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア（Microsoft ExcelやGoogleスプレッドシート）を使いながら具体的に事例を見ていきます。
　必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。

羽山博

筆者紹介： IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。

　データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計（仮説検定編）、第6回です。前回は、正規分布する2つの母集団の分散が等しいかどうかを調べるために、分散の比の検定を行う方法を解説しました。前回までで、母平均の検定、母平均の差の検定、母分散の検定、母分散の比の検定という、よく使われる4つの検定について見てきました。併せて、それぞれの検定における適切なサンプルサイズの求め方も解説しました。

　ただし、Excelにはサンプルサイズを求めるための関数がないので、いちいち数式を入力して計算するか、Pythonでプログラムを作る必要がありました。そこで、今回は無料のG*Powerと呼ばれるツールを使って適切なサンプルサイズを簡単に求める方法を紹介します。

G*Powerをインストールするには

　G*Powerはサンプルサイズを求めるためだけでなく、検出力や効果量を求めるためにも使われます。まず、G*Powerのインストールからです。

　こちら（ハインリヒ・ハイネ大学実験心理学研究所のサイト）にアクセスし、ページの中ほどにある「Download G*Power 3.1.9.7 for Windows」（Windowsの場合）または「Download G*Power 3.1.9.6 for Mac OS X」（macOSの場合）をクリックして圧縮ファイルをダウンロードします（※基本的には最新バージョンをダウンロードすればOKです）。

　Windowsの場合は以下のような手順になります。

• ダウンロードしたGPowerWin_3.1.9.7.zipファイルを右クリックして［すべて展開...］を選択する（指定されたフォルダーにGPowerNT.exeという名前の実行用ファイルが展開される）。
• GPowerNT.exeを実行すれば、G*Powerのウインドウが表示される。

　GPowerNT.exeがうまく実行できない場合は、展開されたフォルダーにあるVC_redistx86.exeを実行し、ランタイム（プログラムの実行に必要なライブラリ）をインストールしてください。G*Powerが実行できるようになります。

　リンクのバージョン番号やファイル名のバージョン番号は今後変わる可能性もあります。また、エクスプローラーの標準設定では、ファイル名の後の「.exe」が表示されていません。プログラムの実行時には、セキュリティ対策ソフトウェアにより「インターネットからダウンロードされたファイルを実行しますか」といった警告が表示されることもあります。公式サイト（上記リンク）から入手したものであれば、通常は安全に実行できます（なお、本稿の手順に基づく操作や実行によって生じたいかなる結果についても、＠ITおよび筆者、Deep Insider編集部では責任を負いかねますので、あらかじめご了承ください）。

　macOSの場合は以下のような手順です。

• ダウンロードしたGPowerMac_3.1.9.6.zipファイルをダブルクリックする（G*Powerという名前の実行用ファイルが同じフォルダーに展開される）。
• G*Powerファイルを実行すれば、G*Powerのウインドウが表示される。

G*Powerを使って母平均の差の検定に必要なサンプルサイズを求める

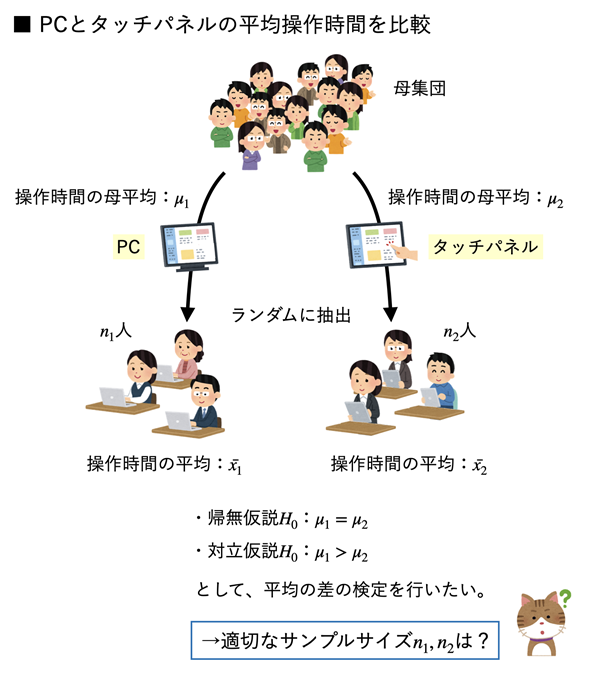
　ここでは、母平均の差の検定を例に、G*Powerの使い方を見ていきます。母平均の差の検定については、この連載の第3回で解説しましたが、念のため事例を紹介しておきます（同じ例だとつまらないので、ちょっと違ったものにしますが、考え方は同じです）。例えば、図1のような場合ですね。あるソフトウェアをPCで操作する場合と、タッチパネルで操作する場合の操作時間では、どちらが速いかを調べたいといった例です。

図1　平均値の差の検定として、想定される事例

母集団からランダムに抽出したサンプルについて、操作時間を測定した結果（

）を基に、母平均（μ₁とμ₂）が異なるかどうかを知りたい。ここでは、PCで操作した群とタッチパネルで操作した群のサンプルは異なる（独立している）。

　ここでは、タッチパネルでの操作がよりスムーズにできる、つまりPCでの操作時間がタッチパネルの操作時間よりも大きくなると考えられるものとします。従って、帰無仮説と対立仮説は以下のようになります。

• 帰無仮説H₀はμ₁ ＝ μ₂
• 対立仮説H₁はμ₁ > μ₂

　検定の方法は以下の通りです。ここで想定される母平均や母分散についても併せて示しておきます。

• 独立した2群の母平均の差の検定（t検定）
• 片側検定
• 有意水準α＝0.05、検出力1−β＝0.8と想定
• 効果量：以下の値を基に後で計算する
• 母平均：μ₁＝55, μ₂＝50と想定
• 母標準偏差：σ₁＝10, σ₂＝12（非等分散を想定）
• サンプルサイズ：n₁＝n₂と想定

　G*Powerの画面でこれらの値を設定していきます。まずは検定の種類の指定と、サンプルサイズを求めるための指定を行います（図2）。

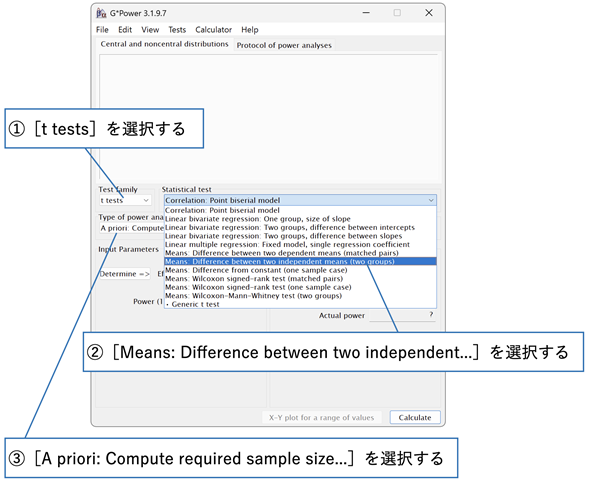
図2　G*Powerの設定（検定の種類や求めたい値を指定する）
この例では、t検定（t tests）で、独立した2群の母平均の差の検定（Means: Difference between two independent means (two groups)）を選択する。分析の方法としては事前のサンプル数の計算（A priori: Compute required sample size - given α, power, and effect size）を選択する。

　図2のように、［Test family］のリストから［t tests］を選択し、［Statistical test］のリストから［Means: Difference between two independent means (two groups)］を選択します。「t検定で、独立した2群の平均の差」ということですね。ここで知りたいのは適切なサンプルサイズなので、［Type of power analysis］のリストから［A priori: Compute required sample size - given α, power, and effect size］を選択します（図ではリストの後ろに隠れていて一部分しか表示されていません）。サンプルサイズの計算を行うに当たって、α、検出力、効果量の指定が必要であることが分かります。

　上のように個々の設定をしなくても、メニューバーから［Tests］-［Means］-［Two independent groups］を選択しても、同じ設定となります。　

　続いて、想定される効果量（Cohen's d）、α、検出力（1−β）、母平均、母標準偏差などを指定します。既にそれらの値が分かっていれば、図3の左側の画面で直接入力すればいいのですが、ここでは効果量が分かりません。そこで、［Determine =>］ボタンをクリックして、想定される母平均と母標準偏差を基に、図3の右側で効果量を計算します。

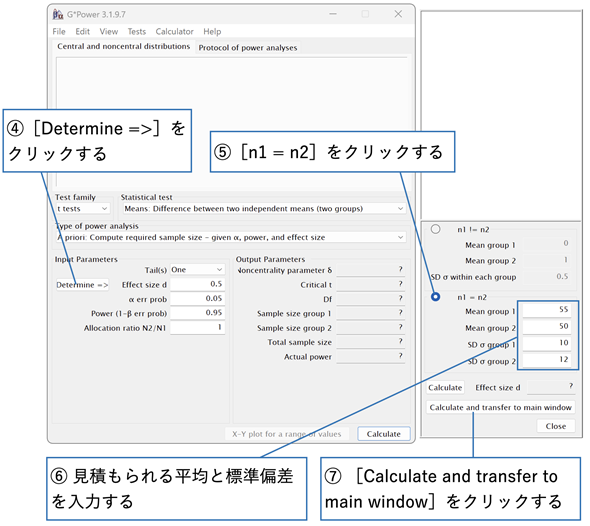
図3　G*Powerの設定（効果量を計算する）
［Determine =>］ボタンをクリックすれば、右側の画面が表示される。サンプルサイズは等しいものとして、各群の母平均、標準偏差として想定される値を入力し、［Calculate and transfer to main window］をクリックすれば、効果量が計算され、左側の画面の［Effect size d］ボックスに表示される（ただし、図は計算前の状態）。

　ここでは、n₁＝n₂を想定しているので、［n1=n2］をクリックし、想定される母平均として［Mean group 1］に一方の群の母平均を、［Mean group 2］にもう一方の群の母平均を入力します。想定される母標準偏差は、それぞれ［SD σ group 1］と［SD σ group 2］に入力します。［Calculate and transfer to main window］ボタンをクリックすれば、効果量が計算され、図4のように［Effict size d］ボックスに表示されます。

　図4は、続けて、［α err prob］にαの値を、［Power(1-β err prob)］に1−βの値を入力して［Calculate］ボタンをクリックしたところです。適切なサンプルサイズが表示されています。

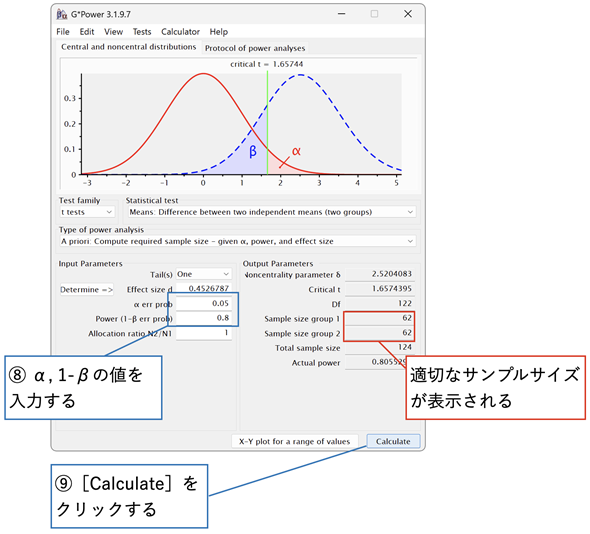
図4　G*Powerの設定（効果量、α、検出力などを指定して、サンプルサイズを求める）
計算された効果量が［Effect size d］に自動的に入力されている。［α err prob］と［Power(1-β err prob)］の値を入力して［Calculate］ボタンをクリックすれば、適切なサンプルサイズが表示される。

　結果はn₁＝n₂＝62となりました。なお、n₁ ≠ n₂と想定される場合は、［Allocation ratio N2/N1］にn₂/n₁の値を入力すれば、それぞれのサンプルサイズが計算されて表示されます。

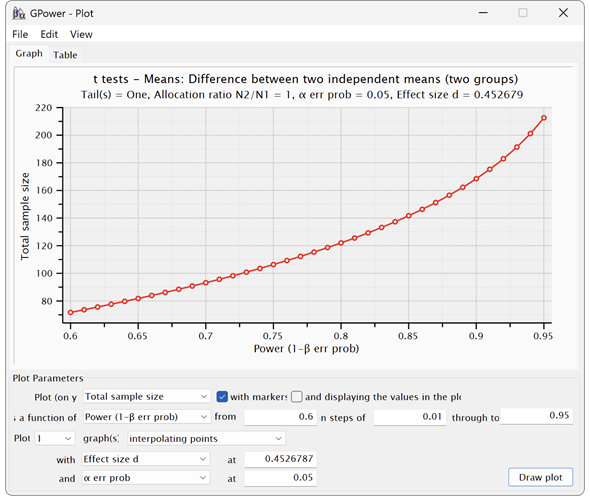
　さらに［X-Y plot for a range of values］ボタンをクリックすれば、［GPower - Plot］というウインドウが表示されます。［Draw plot］ボタンをクリックすれば、図5のようなグラフが表示できます。

図5　検出力とサンプルサイズのグラフ
横軸が検出力、縦軸がサンプルサイズの合計となっている。検出力を0.95とすれば、サンプルサイズの合計は約210となることも分かる（正確には214）。

　［Plot Parameters］の下の［Plot (on y axis)］リストで縦軸を、［as a function of］リストで横軸を指定することもできます（図では表示が一部途切れています）。選択できるのはいずれも［α err prob］、［Power(1-β err prob)］、［Effect size d］、［Total sample size］です。ただし、縦軸と横軸に同じものを指定することはできません。

　G*Powerの便利な機能として、他にも計算機の機能があります。メニューバーから［Calculator］を選択すると、数式を入力できるウインドウが表示されます。単なる電卓機能ではなく、変数や関数なども使えるので、ちょっとした計算や検算に便利です。

　G*Powerにはここで紹介したもの以外にも、さまざまな検定についてのサンプルサイズの計算や、（最初に紹介した）検出力や効果量を求める機能などが備わっています。詳細については、上で示したG*PowerのWebサイトにある「Download the G*Power manual (PDF)」というリンクをクリックして、ドキュメントを参照してください（計算機で使える関数の一覧や、分析の事例などが掲載されています）。

G*Powerを使ってさまざまな検定でのサンプルサイズを求める

　図2〜図5で基本的な使い方が分かれば、後は検定の方法や必要な値を指定するだけで、さまざまな検定での適切なサンプルサイズが求められます。そこで、よく使われるものについて、指定の方法を表1にまとめておきました。いずれも［Type of power analysis］としては［A priori: Compute required sample size - given α, power, and effect size］を選択します。

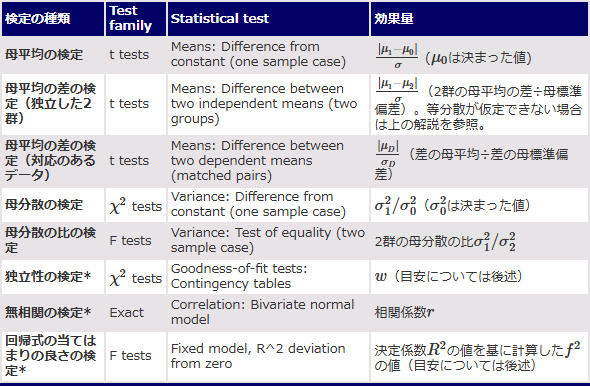
表1　よく使われる検定の種類とサンプルサイズを求めるための指定
*を付けたものはこの連載でまだ取り上げていない検定。今後の連載の中で適宜解説する。表の中で「目安については後述」と書かれた効果量については、それぞれの検定について解説する際に計算方法を解説することとし、以下の表2に目安だけを示す。

　表1の、母分散の比の検定までは、これまでの連載の中で解説しました。*を付けた独立性の検定以降は次回からのお話となります。それらの効果量の計算方法については、どのような検定であるかが分からないと意味が分かりにくいので、今回は取りあえず目安だけを記しておきます（表2）。具体的な効果量の計算方法やサンプルサイズの計算方法は今後の連載で解説することにします。

指標	小	中	大	備考
d	0.2	0.5	0.8	t検定
w	0.1	0.3	0.5	カイ二乗検定。計算方法は次回以降解説
r	0.1	0.3	0.5
f2	0.02	0.15	0.35	計算方法は次回以降解説

表2　効果量の目安
この表で効果量として小・中・大で示した値はあくまで目安。なお、筆者が見た限りでは、分散の検定や分散比の検定に関する目安については、Cohenの著書である「Statistical Power Analysis for the Behavioral Sciences 2nd edition」（J. Cohen, Lawrence Erlbaum Associates, 1988）には記載されていない。G*Powerの設定画面では、t検定なら「Effect size d」、カイ二乗検定なら「w」、相関や回帰分析なら「r」や「f²」など、検定の種類に応じて指定する効果量が異なる。

　繰り返しになりますが、表2に示した効果量はあくまでも目安です。これまでの経験や事例、先行研究などから母平均の差や母分散の比などについて見積もりが可能であれば、その値を使ってサンプルサイズを求めるのが適切です。どうしても見積もりができない場合に限って、上の値を使うということです。

---

　今回は、サンプルサイズを見積もるための便利なツールであるG*Powerを紹介しました。

　次回からは、表1の流れに沿って、さまざまな検定の方法を続けて見ていきます（表1の後には、中央値の検定や分散分析入門なども続きます）。というわけで、次回は、独立性の検定に取り組みます。例えば、出身地域と支持政党に関係はあるのかどうかといった分析を行います。上で「目安」だけを示した効果量wの計算方法についても併せて解説します。次回もお楽しみに！

「やさしい推測統計（仮説検定編）」

AI・データサイエンスの学びをここから

初心者向け、データ分析・AI・機械学習・Pythonの勉強方法　＠ITのDeep Insiderで学ぼう