【Excelで学ぶデータ分析】内向的な人は感受性の幅が広いのか?[架空事例](分布のばらつきの検定):やさしい推測統計(仮説検定編)
初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ(仮説検定編)の第12回。前回から、ノンパラメトリック検定に取り組んでいますが、今回は、分布のばらつきに違いがあるかどうかを検定する方法について解説します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計(区間推定編)」に続く「推測統計(仮説検定編)」です。
この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計(仮説検定編)、第12回です。前回は母集団に特定の母数を仮定しない(できない)場合のノンパラメトリック検定として、順位を基にした中央値の差の検定を取り上げました。今回は、分布のばらつきが異なるかどうかを調べる例として、アンサリ・ブラッドレイ(Ansari-Bradley)検定を取り上げます。また、フリグナー・キリーン(Fligner-Killeen)検定やルビーン(Levene)検定、ブラウン・フォーサイス(Brown-Forsythe)検定と、それらの使い分けについても簡単に触れます。
ばらつきの差の検定とは?
ばらつきの違いを調べたいとき、母集団が正規分布であるという前提の下ではF検定(分散の差の検定)が使えます。しかし、正規性が保証できない場合や、順序尺度のデータである場合、外れ値があるなどの場合には、何らかの確率分布を前提としないノンパラメトリック検定が使われます。今回は、ばらつきの違いを検定する方法として、まず、アンサリ・ブラッドレイ検定を紹介します。
アンサリ・ブラッドレイ検定は、分布の正規性や分布の形が同じであることは前提としていませんが、それぞれの群の中央値が等しいことが前提となっています。その上で、2群の尺度(分布の幅、広がり)が異なるかどうかが検定できるというわけです。図1のような事例を想定してやってみましょう(架空の事例です)。
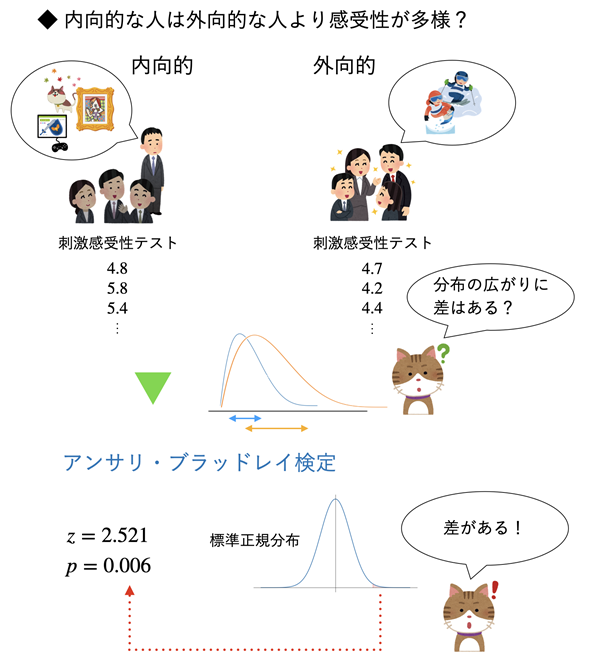
図1 内向的な人は刺激感受性が多様なのか?
内向的な人は絵画や読書などに深く集中し、外向的な人は他者との会話や競技などに広く興味を持つものと考えられる。また、内向的な人は外向的な人に比べて、刺激に対する感受性が強いと言われている。ところで、刺激感受性は人によって異なるのだろうか。
刺激感受性とは、光や音、人混みなど、さまざまな刺激にどの程度敏感か、ということです。一般に、内向的な人は刺激感受性が強いと言われています。では、その幅についてはどうでしょうか。内向的な人と外向的な人には、刺激感受性の幅に違いがあるのでしょうか。つまり、刺激感受性が強い人と弱い人にバラけているのか、ある程度均質なのか、ということです。
もちろん、これからのお話は架空の事例なので、結果を信じてもらっては困るのですが、なんとなく、内向的な人は、刺激感受性の弱い人や、極端に刺激感受性の強い人がいそうな気がします。つまり、ばらつきが大きいのではないかと思われます。というわけで、帰無仮説と対立仮説の確認から始めます。
- 帰無仮説(H0): 内向的な人と外向的な人の分布のばらつきは等しい
- 対立仮説(H1): 内向的な人の方が分布のばらつきが大きい
この例では、内向的な人の方が、分布がばらついているという対立仮説を立てたので、片側検定を行うことになります。
図に示したデータは幾つかの質問項目の平均スコアです。ここでは、集団としての平均的なばらつきを話題にしており、個人ごとの傾向の違い(光に敏感な人もいれば、音に敏感な人もいるといったように質問項目によってスコアに違いがあるということ)を取り上げているわけではありません。また、しつこいようですが、事例はあくまで架空のものです。
ばらつきの差を検定してみよう 〜 アンサリ・ブラッドレイ検定
前回に引き続き、残念なことにExcelにはアンサリ・ブラッドレイ検定を行う関数がありません。もちろん、手順通りに計算すればできるのですが、かなり面倒です。この連載のタイトルに【Excelで学ぶ】とあるので、意地でもExcelでやりたい気持ちはヤマヤマなのですが、あまりにも面倒なので、今回はPythonから利用できるscipy.statsモジュールの力を借りてやってみることにします(感動的なまでに便利です!)。
とはいえ「いや、Excelでやってくださいよ」というムチャ振り(?)にもちゃんと応えたいと思います。Excelでの計算例はこちらに掲載しておきます。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。手順は後のコラムで紹介しますが、具体的な操作方法については[アンサリ・ブラッドレイ検定]ワークシートの中に記してあります。気になる方はチャレンジしてみてください。
さて、Pythonによるアンサリ・ブラッドレイ検定ですが、この事例には前提を満たしていないところがあります。それは、中央値が異なっている可能性があるということです(「内向的な人は外向的な人に比べて刺激感受性が強いと言われている」ということでした)。そのため、中央値をそろえる、という前処理をします。それぞれの群の中央値を求め、各サンプルの値から中央値を引けば、中央値が0にそろいますね。それができれば、後はscipy.statsモジュールのansari関数を呼び出すだけです。
サンプルプログラムはこちらにあります。リンクを開くとPythonのプログラムが表示されるので、最初のコードセルをクリックし、[Shift]+[Enter]キーを押してプログラムを実行すると、結果が表示されます。
import numpy as np
from scipy.stats import ansari
# 刺激感受性テストの結果(xが内向的、yが外向的)
x = np.array([4.8, 5.8, 5.4, 5.2, 4.4, 4.4, 4.2, 5.7, 5.2, 5.4,
4.1, 5.8, 5.6, 4.5, 4.4, 4.4, 4.6, 5.0, 4.9, 4.6])
y = np.array([4.7, 4.2, 4.4, 4.4, 4.5, 4.9, 4.2, 4.6, 4.7, 4.1,
4.7, 4.2, 4.1, 5.1, 5.2, 5.0, 4.4, 4.1, 4.8, 4.5])
# 中央値をそろえる
x_median = np.median(x) # xの中央値
y_median = np.median(y) # yの中央値
x_centered = x - x_median # 各データから中央値を引く
y_centered = y - y_median
# アンサリ・ブラッドレイ検定
w, p = ansari(x_centered, y_centered, alternative='greater')
print(f"検定統計量: {w:.1f}") # 163.0という結果が表示される
print(f"P値: {p:.3f}") # 0.006という結果が表示される
中央値はnumpyモジュールのmedian関数で求められる。各データから各群の中央値を引いて中央値を0にそろえ、それらの値をscipy.statsモジュールのansari関数に指定するだけで検定ができる。xの方が大きいという対立仮説なので、alternative引数に'greater'を指定している。コードを実行すると、UserWarning: Ties preclude use of exact statistic.といったメッセージが表示されることがあるが、これは、厳密な計算ではなく、標準正規分布での近似計算を行っているという意味。
結果は、P=0.006となり、帰無仮説は棄却されます。そこで、対立仮説の「内向的な人の方が分布のばらつきが大きい」を採用します。なお、ここで表示されている検定統計量の163.0という値は標準正規分布に対するz値ではなく、xの順位和(各データに与えた順位の総和)です。
前回やった中央値の差の検定を行って、有意差が出なかった(中央値に差があるとは言えない)という結果が得られたからといって、中央値をそろえずにアンサリ・ブラッドレイ検定を行うのは誤りです。「差があるとは言えない」とは「等しい」ということではありません。また、第一種の過誤の確率を高めてしまいます。
ちなみに、この例で中央値をそろえずに検定を行うと、有意差が出ません。中央値のズレが分布の差を検出する際のノイズとなるからです。中央値が等しいという確たる証拠がないのであれば、上で見たようにあらかじめ中央値をそろえるのが確実です。
コラム アンサリ・ブラッドレイ検定の手順
アンサリ・ブラッドレイ検定の手順はちょっと複雑です。以下に示す式も、文献によって異なり、結果も微妙に違ってくることがありますが、ここでは、scipy.statsモジュールのansari関数と同じ結果が得られる手順を箇条書きで記します。以下、n1をx群(内向的)のサンプルサイズ、n2をy群(外向的)のサンプルサイズ、Nを全体のサンプルサイズ(n1+n2)とします。中央値をそろえる処理は既に行われており、同順位があるものとします。
- 2群のデータをひとまとめにし、値の小さい方と、大きい方から中央に向かって順位aiを割り当てる。
- 例えば、最も小さい値から1位、2位と順位を与え、最も大きい値からも1位、2位という順位を与える。
- 同じ値には順位の平均を与える。
- Excelであれば、RANK.AVG関数を使って昇順の順位と降順の順位の両方を求め、その小さい方を順位の値とするとよい。
- 各群の順位和を求める。x群の順位和をWとする。
- Nが偶数の場合
- Wの期待値E(W)とWの分散Var(W)とを以下の式で求める。
- Nが奇数の場合
- Wの期待値E(W)とWの分散Var(W)とを以下の式で求める
- 以下の式でzを求める。
- zに対する標準正規分布の片側確率または両側確率を求める。
- Excelであれば、=1-NORM.S.DIST(z, TRUE)とすれば片側確率が求められる(zにはzの値が表示されているセルアドレスを指定する)。Googleスプレッドシートの場合は、TRUEという引数がないので=1-NORM.S.DIST(z)とする。
上でも触れたように、この手順で計算した例がExcelとGoogleスプレッドシートのサンプルファイルに含まれています。[アンサリ・ブラッドレイ検定]ワークシートと[アンサリ・ブラッドレイ検定(Nが奇数)]ワークシートの両方を対象に作業してください。
フリグナー・キリーン検定やルビーン検定もばらつきの検定に使われる
お話の内容がかなりニッチになってきましたが、ノンパラメトリック検定でのばらつきの検定には、フリグナー・キリーン検定やルビーン検定、ブラウン・フォーサイス検定などもあります。実は、ルビーン検定とブラウン・フォーサイス検定については、この連載の第5回で既に紹介していました。いずれも、3群以上のばらつきの差を検定できます。ここではそれらの特徴について簡単にまとめるにとどめ、利用例としては、フリグナー・キリーン検定のみ紹介します。
- フリグナー・キリーン検定: 中央値からの偏差によって順位を付ける。正規性は前提としない。分布のゆがみや外れ値があっても適用できる(順位を基にしているので、外れ値に最も強い)。
- ルビーン検定: 平均からの偏差によってF値を求めて検定を行う。正規性は前提としないが、外れ値にはやや弱い。
- ブラウン・フォーサイス検定: 中央値からの偏差によってF値を求めて検定を行う。正規性は前提とせず、外れ値があっても適用できる。
フリグナー・キリーン検定も、Excelでやるにはかなり面倒なので、Pythonでの例を紹介します。……と言っても、scipy.statsモジュールのfligner関数にxとyを指定するだけです。各群の中央値からの偏差によって順位を付けているので、中央値をそろえる必要もありません。
コードは以下の通りです。サンプルプログラムはアンサリ・ブラッドレイ検定と同じファイルに含まれています。リンクを開くとPythonのプログラムが表示されるので、3番目のコードセルをクリックし、[Shift]+[Enter]キーを押してプログラムを実行すると、結果が表示されます。
# フリグナー・キリーン検定
import numpy as np
from scipy.stats import fligner
# 刺激感受性テストの結果(xが内向的、yが外向的)
x = np.array([4.8, 5.8, 5.4, 5.2, 4.4, 4.4, 4.2, 5.7, 5.2, 5.4,
4.1, 5.8, 5.6, 4.5, 4.4, 4.4, 4.6, 5.0, 4.9, 4.6])
y = np.array([4.7, 4.2, 4.4, 4.4, 4.5, 4.9, 4.2, 4.6, 4.7, 4.1,
4.7, 4.2, 4.1, 5.1, 5.2, 5.0, 4.4, 4.1, 4.8, 4.5])
# フリグナー・キリーン検定
s, p = fligner(x, y)
print(f"検定統計量: {s:.1f}") # 6.6という結果が表示される
print(f"P値: {p:.3f}") # 0.010という結果が表示される
scipy.statsモジュールのfligner関数を利用する。xとyをそのまま指定すればよい。ただし、2群以上のばらつきの差があるかどうかの検定なので(引数には、3群以上も指定できるので)、どれが大きいという対立仮説は立てられない(両側検定と同等だと考えてよい)。
使い分けとしては、アンサリ・ブラッドレイ検定は2群で中央値が等しい場合(あるいは中央値をそろえることができる場合)、フリグナー・キリーン検定は3群以上の場合に適しているということになります。外れ値にはいずれも強いですが、2群で片側検定を行いたい場合はアンサリ・ブラッドレイ検定を使うことになります。3群以上のフリグナー・キリーン検定などで、それぞれの群間を比較するには、ボンフェローニの補正などを行って2群ごとに比較する必要があります。
アンサリ・ブラッドレイ検定での適切なサンプルサイズは?
アンサリ・ブラッドレイ検定は母集団の分布を前提としないノンパラメトリック検定なので、サンプルサイズを求めるための決まった公式がありません。また、残念ながらG*Powerのメニューにもありません。正規近似による方法も使われますが、シミュレーションを行って必要な検出力が得られるサンプルサイズを求めるのが確実です。
ここでは、特に前提となる分布を想定していないので、一様分布を使ってシミュレーションを行うことにします。一様分布では、中心から離れた位置にも値がちらばっているので、余裕のあるサンプルサイズが求められるからです。大まかな手順は以下の通りです。
- サンプルサイズn1=5から始める
- サンプルサイズが異なる場合は、n1とn2の比を変えればいいが、ここでは同じサイズとしている
- 以下を繰り返す(デフォルトでは1000回とする)
- xについて、想定される区間を基にn1個の一様乱数を作成する
- yについて、想定される区間を基にn2個の一様乱数を作成する
- 作成した乱数を使って、アンサリ・ブラッドレイ検定を実行する
- 有意になった回数(p<αとなる回数)を数える
- 全体の回数のうち、有意になった回数の割合(=検出力)を返す
- n1の値を増やして(n2の値も増える)、上の繰り返しを行う
- 返された検出力が目標(ここでは、0.8)以上になったら、そのときのn1とn2を出力する
このような流れで作成したコードもこれまでと同じサンプルファイルに含まれています。リンクを開くとPythonのプログラムが表示されるので、4番目のコードセルをクリックし、[Shift]+[Enter]キーを押してプログラムを実行すると、結果が表示されます。
# サンプルサイズの見積り(実行には少し時間がかかります)
import numpy as np
from scipy.stats import ansari
# 乱数をn1個とn2個作成し、n_sim回検定を行い、検出力を求める
def simulate_power(n1, n2, a1, b1, a2, b2, n_sim=1000, alpha=0.8):
np.random.seed(42) # テスト用に乱数の種を固定
reject = 0 # 正しく棄却できた回数
for _ in range(n_sim):
x = np.random.uniform(a1, b1, n1) # ここでは一様分布とする
y = np.random.uniform(a2, b2, n2)
p = ansari(x, y, alternative="greater").pvalue # 片側検定
if p < alpha:
reject += 1
power_calc = reject / n_sim # 検出力(正しく棄却できた確率)
return power_calc
# サンプルサイズの見積りを行う
alpha = 0.05 # 有意水準
power = 0.8 # 検出力
rate = 1 # n1/n2(サンプルサイズの比率)
a1, b1 = -0.7, 0.7 # 群1の区間(スケールが大きい)
a2, b2 = -0.4, 0.4 # 群2の区間
n_start = 5
for n1 in range(n_start, 1000): # サンプルサイズを増やしながら検出力を求める
n2 = np.ceil(n1 * rate).astype(int)
power_calc = simulate_power(n1, n2, a1, b1, a2, b2, n_sim=1000, alpha=alpha)
if power_calc >= power: # 検出力が目標以上になったら
print(f"n1={n1},n2={n1}") # n1=23,n2=23という結果が表示される
break
else:
print("繰り返しの回数を超えました")
上で記した箇条書きの手順に沿って作成したコード。ある程度形の近い分布が想定されるなら、np.random.uniformの代わりに、その分布に従って乱数を作成する関数を指定すればよい(例えば、正規分布ならnp.random.norm関数に平均、標準偏差、作成するサンプルサイズを指定すればよい)。xの想定される区間をa1, b1に、yの想定される区間をa2, b2に指定する。なお、この例では片側検定を想定してシミュレーションを行っているが、事前に、どちらが大きいか強く確信できない場合は両側検定とすべきだ。結果はn1=23, n2=23となる。
今回は、アンサリ・ブラッドレイ検定を中心に、ノンパラメトリック検定によるばらつきの検定の方法を見てきました。パラメトリック検定のための関数はExcelにも備わっていますが、ノンパラメトリック検定の場合は、利用できる関数がないので、Pythonのプログラムや(ここでは触れていませんが)Rなどの統計ソフトウェアを使った方がはるかに簡単です。
さて、次回は、順位相関の検定について見ていきます。今回のニッチなお話よりも、比較的スッキリと理解できるのではないかと思います。次回もお楽しみに!
Copyright© Digital Advantage Corp. All Rights Reserved.