第6回　IntelとCell/B.E.のベクトル演算

ベクトル演算のためのデータ構造

　さて、ベクトル演算を使用する場合、同じサイズの複数データに対して同じ演算を行うわけです。ところで、そのような命令を目的とした既存の従来型プログラムに対して、そのままベクトル演算を適用できるでしょうか。

　整数型や浮動小数点数型のデータが配列としてある場合、ベクトル演算を摘要できる可能性が十分あります。しかし実際は、そのようなプリミティブなデータ型の配列のみを扱ったプログラムだけではありません。

　例えば、複数の場所を表すデータを扱いたい場合には、2次元ならばx、y座標系の、3次元ならばx、y、z座標系、さらに増やしてx、y、z、wなどの構造体やクラスをまず作り、それを要素とする配列を作ることがあります。

　xとyに必ず同じ演算を行うかというと、そうではない場合の方が多々あるかと思いますが、このような配列にはベクトル演算をそのまま適用することは難しくなります。このような構造体の配列をArray Of Structures（AOS）と呼びます。

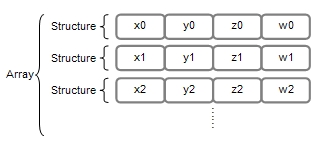
　別の方法として、xだけの配列とyだけの配列というような、本来関連性のある個々のx、y、z、wを分離してしまい、それらを構造体としてまとめることも可能です。

　この場合、x、y、z、wに関する数式であれば、xの配列、yの配列、zの配列、wの配列に対してベクトル演算を適用することができます。このような配列の構造体をStructure Of Arrays（SOA）と呼びます。

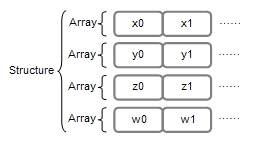
　プログラムのデータがAOSなのかSOAなのかは、ベクトル演算を適用する場合に重要な問題となってきます。CやC++で構造体やクラスが使われている場合は、AOSとなっていることも多くあると思いますが、ベクトル演算による高速化の観点か らはSOAとするのが望ましい形です。

　折衷案として次のようなことが行われる場合もあります。

1. データの保持自体はAOSで行う
2. AOSから複数個のデータを取り出す
3. ベクトル演算用レジスタサイズに合わせてSOAに並べ替える
4. ベクトル演算を適用する
5. 結果をAOSに並べ替えて格納する

　もちろんこの操作を行うことで、元々のアルゴリズムでは必要のない操作が加わりますので、高速化対象となる演算量が少ない場合には遅くなってしまいます。対象部分の演算量が多いかどうかよく見極める必要があります。

簡単なベクトル演算例（SPE on PlayStation 3）

　それではベクトル演算の例として、Cell/B.E.上におけるベクトル演算のコードを見ていきます。PS3へのLinuxのインストールや開発環境のセットアップについてはhttp://cell.fixstars.com/ps3linux/index.php/Cell_SDK_3.1を導入するなど、別の文献に譲りまして、ここではコンパイルができる状態であるという前提で話を進めたいと思います。

#include 
#include <stdlib.h>
#include <math.h>
#include <stdint.h>
#include <assert.h>

#include <spu_intrinsics.h>
#include <spu_mfcio.h>
#include <simdmath.h>

typedef struct
{
    float x, y;
} TwoDim;

void distance_scalar(TwoDim * in0, TwoDim * in1, int size, float * out)
{
    int i;

    for (i = 0; i < size; ++i)
    {
        float x0 = in0[i].x;
        float y0 = in0[i].y;
        float x1 = in1[i].x;
        float y1 = in1[i].y;

        float x2 = (x0 - x1) * (x0 - x1);
        float y2 = (y0 - y1) * (y0 - y1);
        out[i] = sqrt(x2 + y2);
    }
}

void distance_simd(TwoDim * in0, TwoDim * in1, int size, float * out)
{
    int i;
    vector float * v_out = (vector float *)out;

    for (i = 0; i < size; i += 4)
    {
        /* AOS to SOA */
        vector float v_x0 = {in0[i].x, in0[i + 1].x, in0[i + 2].x, in0[i + 3].x};
        vector float v_y0 = {in0[i].y, in0[i + 1].y, in0[i + 2].y, in0[i + 3].y};
        vector float v_x1 = {in1[i].x, in1[i + 1].x, in1[i + 2].x, in1[i + 3].x};
        vector float v_y1 = {in1[i].y, in1[i + 1].y, in1[i + 2].y, in1[i + 3].y};

        /* distance */
        vector float v_x2 = spu_mul(spu_sub(v_x0, v_x1), spu_sub(v_x0, v_x1));
        vector float v_y2 = spu_mul(spu_sub(v_y0, v_y1), spu_sub(v_y0, v_y1));
        v_out[i / 4] = sqrtf4(v_x2 + v_y2);
    }
}

int main(void)
{
    int i;

    TwoDim  input0[1024];
    TwoDim  input1[1024];

    float   scalar[1024];
    float   simd[1024];

    /* initialize */
    for (i = 0; i < 1024; ++i)
    {
        input0[i].x = (double)rand() / RAND_MAX;
        input0[i].y = (double)rand() / RAND_MAX;
        input1[i].x = (double)rand() / RAND_MAX;
        input1[i].y = (double)rand() / RAND_MAX;
    }

    spu_write_decrementer(0xFFFFFFFF);

    /* scalar */
    uint32_t scalar_time = spu_read_decrementer();
    distance_scalar(input0, input1, 1024, scalar);
    scalar_time = scalar_time - spu_read_decrementer();

    /* simd */
    uint32_t simd_time = spu_read_decrementer();
    distance_simd(input0, input1, 1024, simd);
    simd_time = simd_time - spu_read_decrementer();

    printf("scalar_time = %u\n", scalar_time);
    printf("simd_time   = %u\n", simd_time);

    return 0;
}

　このプログラム内容は、2次元座標が2個の配列としてあり、各配列の同一インデックスにある座標間のユークリッド距離を求めています。

　15行目のdistanc_scalar関数は元となるスカラ演算で書かれた距離を算出する関数で、32行目のdistance_simd関数はdistance_scalar関数をベクトル演算で書き直して高速化した関数です。

　distance_simd関数の最初で、34行目のループカウンタ用のiのほかに、35行目でvector floatという型のポインタ変数を定義し、引数のoutの型をキャストして代入しています。

　vector floatというのはSPEに固有の型で、128ビットの領域を4つのfloatとして扱う型です。この型に対してベクトル演算を行います。

　37行目のdistance_simd関数のループでは、39行目でAOSで渡される引数を4個ずつSOAに変換し、v_x0、v_y0、v_x1、v_y1にそれぞれ代入し、その後、45行目で距離の計算を行っています。

　距離の計算にはベクトル演算用の関数であるspu_add、spu_sub、sqrtf4を用いています。spu_mulは2つのvector型の掛け算を行い、spu_subは2つのvector型の引き算を行う組み込み関数です。また、sqrtf4は1つのvector型の平方根を計算するsimdmath.hに定義された関数です。これらの関数を使用することでベクトル演算が行われます。

　main 関数では、62行目で入力用の座標を疑似乱数で初期化し、75行目のdistance_scalarおよび80行目のdistance_simdの前後で、実行時間を計測するためにspu_read_decrementerという関数でSPEに付属するデクリメンタの値を取得しています。

　このデクリメンタは一定時間ごとに値が減っていくカウンタなのでspu_read_decrementerを使用する前に、spu_write_decrementerを使って0xFFFFFFFFで初期化してから使用します。

　最後に、デクリメンタの値でどのくらいの実行時間がかかったかを表示します。

　このソースコードをsimd_spu.cという名前で保存し、コンパイルします。

spu-gcc -W -Wall -O3 simd_spu.c -o simd_spu.elf -lm -lsimdmath

　実行結果は次のとおりです。SPEのコードはコマンドライン上から直接実行することができず、一般的にはSPEコードを呼び出すためのPPE側コードが必要となりますが、今回はコードの簡略化のためelfspeというコマンドによりSPEのコードを実行させます。

$ elfspe simd_spu.elf
scalar_time = 5940
simd_time = 994

　約6倍弱の高速化となりました。1つのfloat演算だったものを4つ同時にfloat演算するようにしたので、ちょうど4倍になるはずと思われるかもしれませんが、SPEはベクトル演算を基本としているため、スカラ演算のみで書かれたコードはやや無駄な処理が行われ、SPEの特性に合わせて素直にベクトル演算で書くことで4倍以上速い結果となっています。

2/2

Index
IntelとCell/B.E.のベクトル演算
	Page1 ベクトル演算を使った高速化 Intel SSE演算器 Cell/B.E. SPE ベクトル演算器
	Page2 ベクトル演算のためのデータ構造 簡単なベクトル演算例（SPE on PlayStation 3）

Think Parallelで行こう！