連載

2003年6月24日

ブロックアルゴリズムとB-Treeアルゴリズム：Linuxファイルシステム技術解説（2）（3/3 ページ）

長らく標準ファイルシステムとしてLinuxを支えてきたext2の仕組みを明らかにするとともに、ext2の問題点を克服するための諸技術について解説する。（編集局）

[菅谷みどり，＠IT] PC用表示関連情報

LINE

Hatena

前のページへ | 　　　　　　

ファイルサーチを高速化するB-Treeアルゴリズム

　ext2、ext3がベースとするブロックアルゴリズムは、ブロック数が対応するディスクのジオメトリ数に制限されること、ファイルサーチにO（n）かかる（注）こと、ファイルサイズに関係するパフォーマンス低下など、いくつかの問題があった。

注：「O（n）」とは、実行時間が入力の大きさ「n」に比例するアルゴリズムである。O（n）は「nのオーダー」または「オーダーn」と読む。後述する「O（log n）」は、アルゴリズムの計算量に関する議論の場合logの底は常に2で、O（log n）の方がO（n）よりも効率が良い。例えばn＝8の場合、O（log n）は入力8に対して3回の実行で済むが、O（n）は8回の実行となる。

　ReiserFS、JFS、XFSといったファイルシステムでは、こうしたブロックアルゴリズムの限界に対して、早い段階からデータベースの技術をファイルシステムに取り込んでいた。データベースの分野では、ファイルシステムとは比較にならないほど大量の情報を素早く検索し、しかもデータの追加や変更も簡単に行えるような設計の研究が長年続けられてきた。ここでは、ReiserFS、JFS、XFSで利用されている「B-Tree」アルゴリズムについて解説し、その派生形として「B*-Tree」「B+-Tree」について述べる。

B-Treeとは

　B-Treeは、Balanced Tree（バランス木）の略で、木構造（注）のインデックスツリー（索引木）により検索を高速化するアルゴリズムである。Binary Trees（二分木）を改善した手法として1970年代に登場して以来、長年にわたってデータベースやファイルシステムなどで利用されている。パフォーマンスについては、O（n）であるブロックアルゴリズムに対してO（log n）で行えるという圧倒的な優位性がある。

注：木構造はデータアクセスのためのアルゴリズムの1つで、空でない接点（ノード：node）の集合と辺（枝：edge）で構成された、木の形をしたデータ構造を持つ。最上位層のノードを根（root）、最下位層のノードを葉（leaf）と呼び、これらが相互にポインタによってリンクする。「Balanced Tree」は、ルートから各リーフまでの階層数をすべて同じにする木構造をいう。

　B*-TreeやB+-Treeは、B-Treeのバリエーション（派生形）である。B-Treeは本来O（log n）のアルゴリズムであるが、削除や挿入を繰り返すと最大O（n）になってしまう問題点があるため、これを改善する手法として登場した。「*」や「+」は、B-Treeのオリジナルバージョンから変更が加わっていることを示す。B*-TreeやB+-Treeによって、データベースはスケーラビリティとレコードに対するアクセスの向上が図られている。B*-TreeはReiserFSで用いられ、B+-TreeはJFSとXFSで利用されている。

Binary Treeの問題点

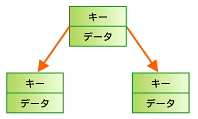
図4　Binary Treeノード

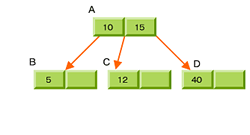
　B-Treeのさらに基となるBinary Tree（二分木）は、木構造アルゴリズムの中で最もシンプルな構造である。各ノードはキーとデータのペアで構成され、0?2つの接点（子：child）を持つ（図4）。子はさらに子を作ることができ、子の作成を何度も繰り返すことで木全体の規模は大きくなっていく。

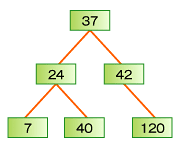
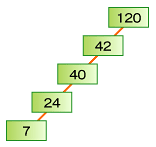
　二分木探索では、あるノードのキー値がKの場合、そのノードのサブツリーに格納されているすべてのノードのキー値はKより小さく、右サブツリーに格納されているのすべてのノードのキー値がK以上である二分木を探索する。図5は「37、24、42、7、40、120」の順、図6は「120、42、40、24、7」の順番で値が挿入されている。この状態で「7」のデータを検索する場合、図5であれば2回で目的のデータにたどり着けるのに対し、図6ではデータの個数である5回のデータアクセスが必要となる。

図5

図6

　このことからも二分木はできるだけバランスしている状態が望ましく、特に木が低い（階層が浅い）方が良いことが分かる。nノードの二分木がバランスしているとき、高さはおよそlog nになる。一方、最悪にバランスの取れていない木は高さがnになる。バランスしている場合は最悪でもO（log n）のオーダーであるが、バランスが悪い場合はO（n）となってしまうのである。

常にバランスするB-Tree

　B-Treeは、常にバランスすることが特徴である。オリジナルの二分木から改善された点としては、

ノードが複数のキー値を持つ
これにより、木は二分木とはならない
ノードは二分木のノードに類似している
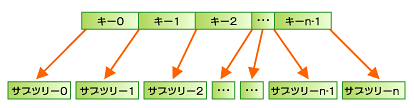
ノード内のキー値は常に次のような順序になっている
キー0＜キー1＜キー2……＜キー（n-1）

図7　B-Treeノード

　探索を行う場合は、ルートノードから始めてキー値をたどってゆく。ルートノードのキー値（キー0?キー（n-1））はソートされており、キー値が指し示すサブツリー（n-1）は必ずサブツリー（n-2）よりも大きいことが保証される。新しいデータを追加する際、キーnよりも大きい場合は右、小さい場合は左のサブツリーにマージされる。ツリーにデータを追加する際に、データの追加によって右左のノード数のバランスが悪くなる場合は、連鎖的に親ノードにマージすることでバランスを取る。この様子を以下の例で見てみよう。

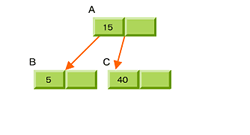
ノード内のキー値が「2」の場合の例

*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***

1.ノード内でソートして格納

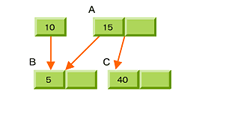
2.ノ子ノードの作成（ノードが形成される）

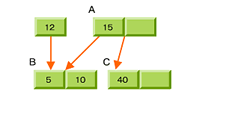
3.ノノードBにデータが追加される（1回目）

4.ノノードBにデータが追加される（2回目）

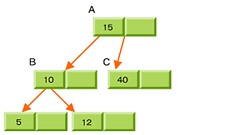
5.ノノードBは分割される→バランスが悪くなる

6.ノ親ノードAにBがマージされる→バランスする

　このように、B-Treeではインデックスが増えると分割が起こり、さらにバランスが悪くなると上位にマージされるという動作を繰り返すことで、最終的に左右のバランスが均衡する。バランスがよい木構造はlog nの値を小さくできるので、アルゴリズムとしても効率が良い。また、B-Treeではノード内のレコードをグループ化してソートする。これにより、目的のファイルに高速にアクセスできる。

**ReiserFSのB*-Tree**

　B*-Treeでは、B-Treeの2つのノードをさらに3つに分割するという方法を取る。B-Treeよりもレコードに対するノードの充足率を高めるため、スペース効率が良くなる。

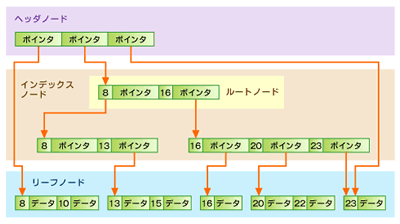
　レコードには、キー値とデータブロックへのポインタという2つのフィールドを持たせる。図8は、一般的なリーフのインデックスノードのデータ構造である。

図8　インデックスノードのデータ構造

　全体は「ヘッダノード」と「インデックスノード」、そしてデータが保持される「リーフノード」に分けられる。ヘッダノードはノード0で、B*-Treeについてのすべての情報を保持している。

　例えば、20のキー値を持つデータレコードを検索するケースを図9で見てみよう。ファイルマネージャは検索をルートノードから始める（1レベルの場合、ヘッダノードとインデックスノードは等しくなる）。検索キー値以下もしくは等しいキー値が見つかるまで、右に移動しながら順番にレコードを見ていく。見つかったら、ポインタが指している一段下のノードに移動する。図9の場合、インデックスノードは「8＜20」なので右に移動し、次に「16＜20」であるが次がないので16のポインタをたどって次のレコードを探す。右に移動すると、「20＝20」で目的のデータが見つかったので、ポインタが指すリーフノードを得る。検索キー値が見つかると同時に、データも発見できるというわけだ。

図9　B*-Treeによる検索例

　ファイルシステムでは、B-Tree自体がiノードの代わりとなる。そのため、固定したiノードを持たなくても、ノードの必要性に応じて領域を確保する動的iノードを実現している。

JFS／XFSのB+-Tree

　B+-Treeはリレーショナルデータベースで用いられているISAM（Indexed Sequential Access Method）とB-Treeの特徴を併せ持った方式である。

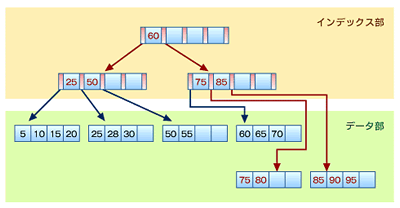
　B+-Treeは名前からも分かるように、B*-Tree同様バランス木を構成する。B*-Treeと異なる点は、B+-Treeはデータとキーを完全に分けて管理していることである。B+-Treeは図10のようにノードの下位層をインデックス部とデータ部に分けて構成し、「データ」は常にリーフノードに保存する。インデックス部の各ノードは4つのキー値と5つのポインタのみを保持する。

図10　B+-Treeの構造

　リーフ部には、キー値のソート順に従って実際の「データレコード」が格納されている。レコードの先頭キー値に対するインデックスが、ツリー内に構成される（図中の25、50、75、85は先頭キー値）。多数のキー値をインデックスとして持つことで、ツリーのパスを短くでき、結果的に目的のデータまでのアクセス回数を減らすことができる。また、インデックス部にデータを持たないため、インデックス部のデータ容量が少なくて済む。

　インデックスはデータのように書き込みを必要としないため、メモリ上に配置して高速検索を実現できる。特に、XFSではフリーブロックの管理などもB+-Treeで行っており、大きな空き領域の高速アクセスなどに威力を発揮している。

　今回は、ブロックアルゴリズムとB-Tree（とその派生技術）を解説した。次回は、より効率的なアドレッシング方式であるエクステントをはじめ、ファイルシステムの標準機能になりつつあるジャーナリングについて説明する。

「次回」へ

「Linuxファイルシステム技術解説」バックナンバー