現在の計算機能力だけで解ける暗号強度はどのくらいか
上述したように、最良の攻撃方法を利用したときの強度で安全性の上限が決まってしまう以上、現状あるいは近い将来の計算機能力だけを用いて、最良の攻撃方法を利用したときに解ける暗号強度を知っておくことは、安全性の上限として十分であるかどうかを判断するうえで極めて重要である。
この観点から、共通鍵暗号ではRSA LaboratoriesがDES challenge[参考文献3]やThe RSA Laboratories Secret-Key Challenge[参考文献4]を主催し、鍵全数探索法を利用してどの程度の時間で共通鍵暗号が解けるかのコンテストを実施している。前者はDES(鍵長56ビット)を、後者はRC5(鍵長は40〜128ビット)が対象である。
これらのコンテストで主体的な役割を果たしているのがElectronic Frontier Foundation(EFF)とDistributed.netである。EFFはDES解読装置DES Crackerを作成してDES解読を成功に導いた実績があり、またDistributed.netも暗号解読のためのプログラムを作成・公開し、世界中のボランティアから提供された多数の計算機上でそのプログラムを走らせて解読成功に導いている。
彼らの結果を中心に、共通鍵暗号の鍵全数探索攻撃による解読実績を表2に示す。ちなみに、Distributed.netが現在実施している鍵長72ビットRC5解読プロジェクトでは、1秒間に約1390億個(=約237個)、1年当たり約262個の秘密鍵の検査が可能な計算機能力が世界中のボランティアから実際に提供されている[参考文献5]。
*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***
公開鍵暗号でも同様のコンテストを実施しており、有名なところでは、RSA LaboratoriesのThe New RSA Factoring Challenge[参考文献6]、WagstaffのThe Cunningham Project[参考文献7]、CerticomのThe Certicom ECC Challenge[参考文献8]などがある。前2つは素因数分解問題へのチャレンジであり、さまざまなパラメータに対しての素因数分解が試みられている。最後のものはだ円曲線上の離散対数問題へのチャレンジである。
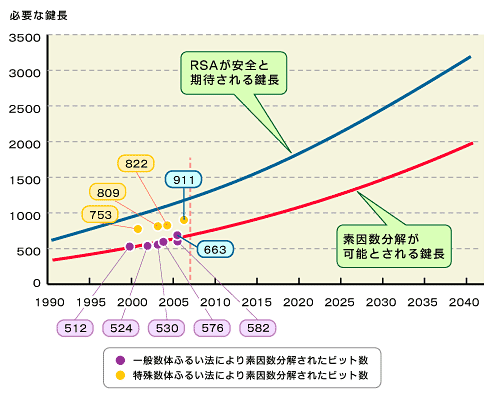
現在、素因数分解問題へのチャレンジで主体的な役割を果たしているのが、ボン大学を中心とするドイツチームと立教大・NTT・富士通研究所を中心とする日本チームである。ドイツチームは数体ふるい法を利用して663ビットの一般合成数の素因数分解記録を、日本チームは特殊数体ふるい法を利用して911ビットの特殊合成数の素因数分解記録をそれぞれ保持している。彼らの結果は、図1に示すように、数体ふるい法が最良の攻撃方法であると仮定したときのLenstra[参考文献9]やBrent[参考文献10]らによる素因数分解の成功予測曲線とほぼ一致していることが確認できる。
また、素因数分解問題以外では、現在までに指数計算法を利用した607ビットの有限体上の離散対数問題とρ法を利用した109ビットのだ円曲線上の離散対数問題が解かれた実績がある。
Copyright © ITmedia, Inc. All Rights Reserved.