「27°C×2＝54°C」が何の意味もない理由とは――「測定」と「データ」の基礎知識：「AI」エンジニアになるための「基礎数学」再入門（2）（2/2 ページ）

AIに欠かせない数学を、プログラミング言語Pythonを使って高校生の学習範囲から学び直す連載。今回から具体的に数学を学ぶと予告しましたが、まずは「測定」と「データ」の基礎知識について押さえておきましょう。

[西村圭介，東京ITスクール]

誤差とバイアス

　データの種類と特徴を学んだところで、データ分析やAI構築に踏み出す前に、「そもそも、そのデータは使うに値するものなのか？」と疑うことは非常に大切なステップです。なぜならば、使うに値しないデータ――極端な話、ランダムに生成された数字――をどれだけ分析したところで、有用な情報が得られるわけがないからです。

　では、「どのような観点からデータの有用性を疑うべきなのか」というと、大まかに「誤差」「バイアス」の2つの観点があります。

誤差

　データは、「データ = 真の値 + 誤差」で生成されます。常に真の値が測れればいいのですが、どれだけ精細なモノサシやセンサーを用いても、測れる値の細かさには限界がありますので、寸分の狂いなく真の値を測ることは基本的には不可能です。しかし、誤差が真の値に比べて大き過ぎては、生成されたデータは使いものになりません。

　誤差の中には、発生してもあまり問題のない（やむを得ない）誤差である「偶然誤差」と、なるべく発生しないように努めなければいけない誤差である「系統誤差」が存在します。

　それぞれの性質をよく理解し、自分が扱うデータは扱うに妥当なものなのか否かを見極められるようになりましょう。

・偶然誤差

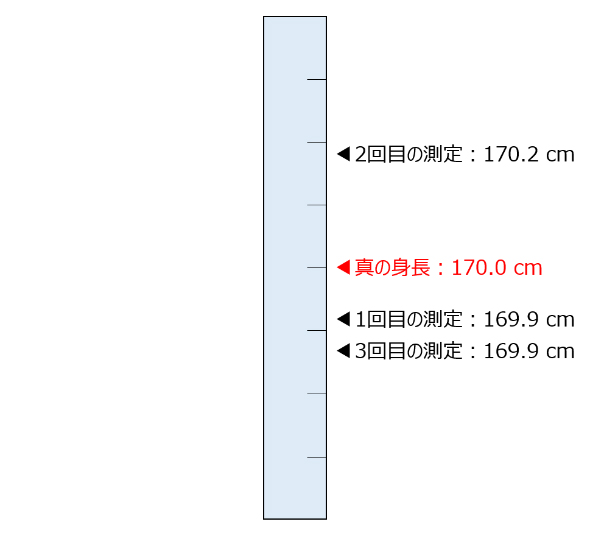
　偶然誤差とは、ランダムかつ平均が0の誤差のことを指します。これについては、身長測定を例にして説明します。仮に、正しい身長測定の方法があり、それを採用すると系統誤差が0になる（現実的には難しい）測定法を実践したとします。そうした時のイメージが図4です。真の値を中心にランダムに誤差が発生していることをイメージして作図しました。

図4　偶然誤差の例

　偶然誤差は、恐るるに足らずで、値を複数回測定した上で、その値の平均を取ってしまえば、誤差の影響を除去できます。例えば図4では、身長を3回測定しており、その平均値は170.0センチということで偶然誤差の影響を除去しつつ真の値を測定できていることが分かります。

　なお、計測1回当たりの偶然誤差を小さくしたければ、より目盛りの細かい測りを使ったり、精緻なセンサーを使うなどの対応が考えられます。

・系統誤差

　系統誤差は、偶然によらず、何かしらの理由があって発生する誤差です。どのような誤差なのかを偶然誤差と対比しながら確認しましょう。

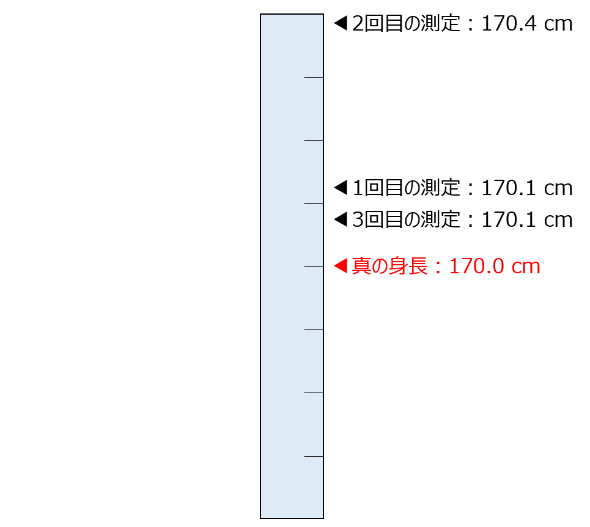
　ここでは、不適切な身長の測定方法で、測定器の目盛りを頭頂ではなく、髪の毛に触れる点で止めて計測してしまっているケースを考えます。このケースだと、真の値と計測値の関係は図5のようになるでしょう。

図5　系統誤差の例

　このように、偶然誤差を差っ引いたとしても、誤った測り方によって計測値が真の値よりも上振れ――平均は170.3センチとなる――してしまっていることが分かります。この上振れしてしまっている要素が系統誤差です。つまり、この上振れの原因は、「目盛りを置く位置が不適切である」という明確な理由があり、解消できる誤差です。

　この場合であれば、計測者に計測方法を指導したり、複数人が測定した値の平均を取ったりすることで、系統誤差の影響を小さく――ある人は大きめの値を取る癖があり、ある人は小さめの値を取る癖がある場合に0に平均化するなど――できます。

バイアス

　バイアスとは、「偏り」を意味します。上で述べた誤差よりも恐ろしい概念で、バイアスが存在するデータを用いた分析結果やAIは時に無価値になってしまうこともあります。

　バイアスについては世論調査を例に確認しましょう。

図6　1936年アメリカ大統領選挙の事前調査と実際の開票結果

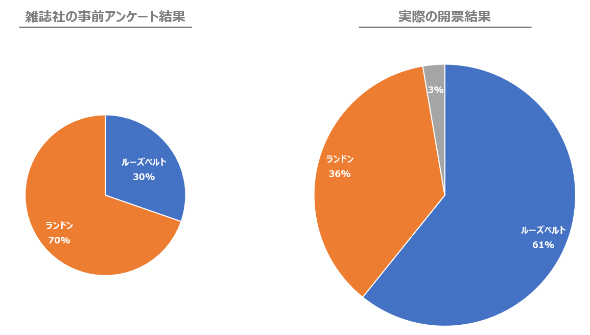
　図6は1936年に行われたアメリカ大統領選挙で、雑誌社が行った事前アンケート結果と、実際の投票結果を比較したものです。雑誌社は、雑誌の定期購読者などにハガキを送り、「共和党のランドン氏と民主党のルーズベルト氏のどちらに投票するか」の回答を200万人以上集めました。

　大量のデータを集めたにもかかわらず、なぜ実際の結果と懸け離れた調査結果になったのでしょうか。そこにはバイアスが大きく関係してきます。

図7　バイアスの例

　この例では、雑誌社の調査結果が大きく実際と異なった原因は、データを取る対象にありました。「雑誌の定期購読者などにハガキを送り……」と前述しましたが、ここに落とし穴があります。実は、この定期購読者には富裕層が多く、その富裕層の世論は図7のように、大きく全体の世論とは懸け離れたものでした。

　このように、雑誌社のアンケート結果には富裕層のバイアスがかかっていたために無価値――アンケート結果は開票結果の予想として見られると仮定すると無価値です――になってしまったわけです。

　データ分析は主にビジネス上の意思決定に使われるので、このようなバイアスがかかったデータから出力された分析結果を基に意思決定をすることは非常に危険です。常に分析の目的（この例では「富裕層に絞った世論が知りたい」という場合なら問題ありません）と、「使用するデータが分析するにふさわしいか」をバイアスというキーワードの下にうたぐっていくことが大切です。

次回は「基本統計」と「データ加工」

　次回は、「基本統計」と「データ加工」の手法について解説します。基本統計では、今回の記事の所々で出現した「平均値、中央値……」といったキーワードについての定義や利用法を紹介する予定です。データ加工では、欠損値のあるデータへの対応方法や、質的データを比例尺度へと変換する技術などを紹介します。本稿を読んでいると、それら手法の必要性や有用さの実感が増すと思います。次回もご期待ください。

筆者紹介

西村圭介

1991年、富山県生まれ。大学院を卒業し、企画コンサルタントとしてキャリアをスタートする。その後、統計学とプログラミングスキルの知見を基にデータサイエンティストとしてのキャリアを進める。現在は東京ITスクールの講師として、実務レベルのデータサイエンティスト輩出を目的としたAI研修に努める傍ら、分析や機械学習を用いたマーケティング支援を行う。