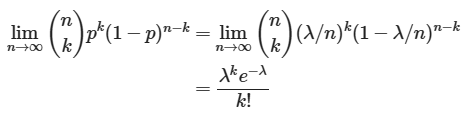[データ分析]ポアソン分布 〜 100年に1人の天才は何人現れる?:やさしい確率分布
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(確率分布編)の第4回。ポアソン分布とは、出来事(事象)が、まれにしか起こらない場合に、独立な試行を何回も繰り返したときの確率分布です。そのような事例を紹介した後、確率の求め方や可視化の方法などを解説していきます。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載(記述統計と回帰分析編)の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば(すり抜けキケン、制限速度守ってね!)。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第4回です。前回は、福引などのように、引いたくじを元に戻さない非復元抽出の例と、その確率分布である超幾何分布を取り上げました。今回は、まれにしか起こらない事象の例を紹介した後、その確率分布であるポアソン分布を取り上げ、その意味や特徴などを見ていきます。
100人に1人の天才は何人いる?
「最近の日本人で100年に1人の天才は」というと、皆さんは誰の名前を思い浮かべるでしょうか。ChatGPTに聞いてみたところ、将棋の藤井聡太、野球の大谷翔平、医学者の山中伸弥が例として挙がりました(敬称略、以下同様)。オレンジ色の部分をクリックまたはタップするとChatGPTの答えが表示されます。皆さんが思い浮かべた人と一致したでしょうか(実際のChatGPTでは、質問の仕方などによって違う名前が表示されるかもしれません)。
日本人と限定せずに聞いてみたところ、アインシュタイン、レオナルド・ダ・ヴィンチ、モーツァルトの名が挙がりました。歴史上の人物なので、1000年に1人といった方が適切かもしれませんね。今回登場するポアソン分布の式を導出したフランスの数学者シメオン・ドニ・ポアソンも、天才の一人かもしれません。ちなみに、筆者は、数学者ペレルマンの名前を挙げます。
それにしても、さまざまな分野で100年に1人の天才が登場しますね。その確率分布について考えてみましょう。100年間で平均して1人の天才が登場することが分かっているものとして、100年間のうちに2人の天才が現れる確率はどれぐらいでしょうか。
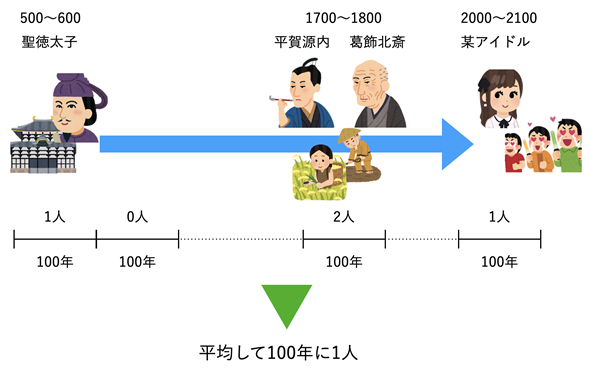
図1 100年に平均して1人の天才が登場するイメージ
平賀源内の生年は享保3(1728)年、葛飾北斎の生年は宝暦10(1760)年。なお、イラストに時代背景の異なるもの(飛鳥時代の聖徳太子《厩戸王:うまやどのおう》と奈良時代の東大寺など)があるがご容赦のほど。
このような、まれにしか起こらない事象の確率はポアソン分布(Poisson distribution)と呼ばれる確率分布に従います。ポアソン分布では各試行は独立であることが前提となっています。まずは理屈抜きで、以下に示すポアソン分布の確率質量関数の式に当てはめて、確率を求めてみましょう。
(1)式のkが確率変数の値です。つまり、何人天才が現れるかということですね。この場合は、100年間のうちに2人の天才が現れる確率なので2です。
λ(ラムダ)は事象が起こる平均の数です。この場合は、平均して1人なので1ですね。
eは自然対数の底で、e=2.7182…という値です。
ただ、細かい計算になるので、実際に計算していただかなくても構いません。数式中のλとkにどのような値を指定すればいいのかを確認しておいてください。オレンジ色の部分をクリックまたはタップすると答えが表示されます
答え: ア= 1 、イ= 2
第1回でも簡単に触れましたが、確率分布の形状を決定する定数値(例えば平均や標準偏差など)は母数(パラメーター)と呼ばれます。ポアソン分布の母数(=ポアソン分布の確率質量関数を一意に決める値、つまりその確率分布の形状を完全に決定する値)はλであることも確認しておいてください。なお、kは確率変数の値(ある事象が起こる回数などの具体的な数値)であり、母数(パラメーター)ではありません。
コラム まれにしか起こらないってどういうこと? 〜 二項分布とポアソン分布の関係
すでに述べたように、ポアソン分布はまれにしか起こらない事象が起こる場合に、その事象が何回起こるかを求めるのに使われる確率分布です。しかし、「まれにしか起こらない」というのはずいぶんとあいまいな表現ですね。その意味を明確にしておきましょう。
実は、二項分布の試行回数をn、成功確率(目的の事象が起こる確率)をp=λ/nとし、λを一定のままとし、試行回数nを無限大に近づけていくと(その場合、pが小さくなっていきます)、平均λのポアソン分布になります。このことを式で表すと以下のようになります。
この式にある最初の( )は、組み合わせ数を表します。計算方法については、第2回の記事で説明しましたので、忘れた場合はそちらを復習してください。
この式の証明は高校数学の知識でできますが、やや難しいので省略します。ここでは、目的の事象が起こる確率pが小さい=試行回数nに比べ、事象が起こる回数λが小さい、ということが「まれにしか起こらない」ということだと理解していただければよいかと思います。このことについては、次の項で関数とグラフを使って確かめてみます。
ところで、二項分布の特殊な形であるなら、何もポアソン分布なんて使わずに二項分布だけで事足りるのでは、と思われるかもしれません。しかし、それぞれの確率密度関数(上の式の左辺と右辺)を見比べてみると、右辺のポアソン分布の方が簡単で、計算が楽であることが分かります。また、母数も二項分布ではnとpの2つですが、ポアソン分布ではλだけなので、母数の推定も簡単であるなどのメリットがあります(母数の推定については推測統計編でお話する予定です)。
ポアソン分布の確率質量関数と累積分布関数を可視化してみよう
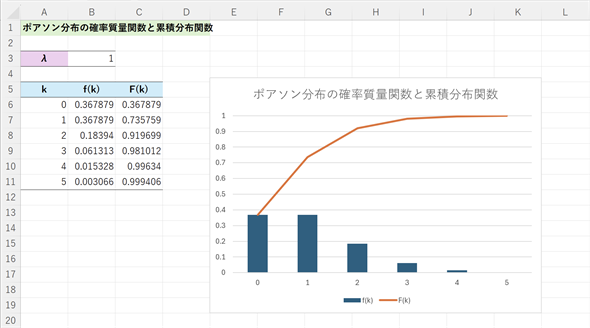
ここまでは、100年に1人の天才が2人現れる確率だけを見てきました。つまり、確率変数の値k=2の場合だけでした。当然のことながら100年に1人の天才が現れない(k=0である)場合もあるわけです。そこで、k=0〜5までについてポアソン分布の確率質量関数と累積分布関数を可視化してみましょう。
(1)式を使って計算することもできますが、ExcelのPOISSON.DIST関数を使えば簡単です。結果は図2のようになります。作成の手順は図2の後に記しておきます。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、[ポアソン分布]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。具体的な操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB6に=POISSON.DIST(A6:A11,B3,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルB6〜B11)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルC6に=POISSON.DIST(A6:A11,B3,TRUE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルC6〜C11)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルB5〜C11を選択する
- [挿入]タブを開き、[複合グラフの挿入]ボタンをクリックして[集合縦棒 - 折れ線]を選択する
- [グラフのデザイン]タブを開き、[データの選択]ボタンをクリックする
- [データソースの選択]ダイアログボックスで[横(項目)軸ラベル]の下の[編集]ボタンをクリックする
- [軸ラベル]ダイアログボックスで[軸ラベルの範囲]ボックスをクリックし、セルA6〜A11を選択する
- [OK]をクリックして[軸ラベル]ダイアログボックスを閉じる
- [OK]をクリックして[データソースの選択]ダイアログボックスを閉じる
POISSON.DIST関数の引数は図3のように指定します。母数がλだけなので簡単ですね。
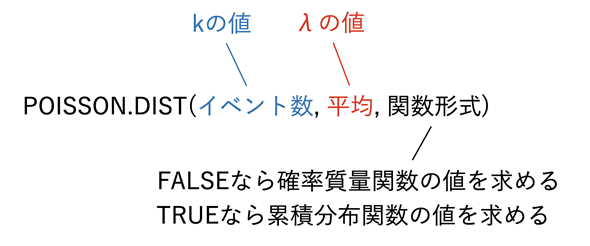
図3 POISSON.DIST関数に指定する引数
図2の例では、イベント数としてA6:A11というセル範囲を指定しているので、スピル機能によりセルA6〜A11のイベント数に対する確率質量関数の値や累積分布関数の値が一度に求められる。イベント数とは、目的の事象が起こる回数、つまりkに当たる値のこと。
なお、サンプルファイルには、(1)式に従って確率質量関数と累積分布関数の値を求めた例も[ポアソン分布 (公式に従って作成)]ワークシートに含めてあります。興味のある方はご参照ください。
上のコラムでも述べたように、二項分布でp=λ/nとし、λを一定のままとし、試行回数nを無限大に近づけていくと、平均λのポアソン分布になります。例えば、100年に1人の天才が現れるなら、n=100、λ=1なので、p=1/100です。
そこで、n=100、p=1/100の二項分布の確率質量関数と、λ=1のポアソン分布の確率質量関数についてk=0〜10までの値を求め、可視化してみましょう(図4)。サンプルファイルの[二項分布とポアソン分布]ワークシートを開いてください。作成の手順は図4の後に記しておきます。
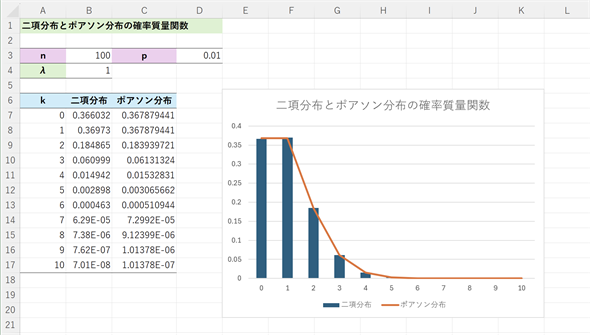
図4 nの値が大きくpの値が小さいときの二項分布とλ=npのポアソン分布
二項分布の確率質量関数を棒グラフで、ポアソン分布の確率質量関数を折れ線グラフで描いてみた。n=100の場合でも、二項分布とポアソン分布がほぼ重なることが分かる。n=1000やn=10000にすると、さらに値が近づく(セルB3の値を変えて試してみるとよい)。
◆ Excelでの操作方法
- セルD3に=B4/B3と入力する
- セルB7に=BINOM.DIST(A7:A17,B3,D3,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルB7〜B17)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルC7に=POISSON.DIST(A7:A17,B4,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルC7〜C17)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルB7〜C17を選択する
- [挿入]タブを開き、[複合グラフの挿入]ボタンをクリックして[集合縦棒 - 折れ線]を選択する
- [グラフのデザイン]タブを開き、[データの選択]ボタンをクリックする
- [データソースの選択]ダイアログボックスで[横(項目)軸ラベル]の下の[編集]ボタンをクリックする
- [軸ラベル]ダイアログボックスで[軸ラベルの範囲]ボックスをクリックし、セルA7〜A17を選択する
- [OK]をクリックして[軸ラベル]ダイアログボックスを閉じる
- [OK]をクリックして[データソースの選択]ダイアログボックスを閉じる
ポアソン分布の応用例
これまで、一定の期間である事象が起こる確率を見てきました。ポアソン分布は他にも、お昼時の1時間に平均10人の顧客が訪れる(λ=10の)店舗で、1時間にk人の顧客が訪れる確率を求めたり、10000個の製品の中で平均1個の不良品が発生する(λ=1の)場合に、10000個中k個の不良品が発生する確率を求めたりするのに使えます。100連ガチャを引いたときにレアアイテムが幾つか得られる確率なども求められますね。
店舗の例であれば、お昼時に多くて何人の顧客が訪れるかを見積もることができ、店員の最適な配置などに利用できます。この場合、1時間に18〜20人の顧客が訪れる確率を計算すると以下のようになります(サンプルファイルの[ポアソン分布 (応用例)]ワークシートにk=0〜20の場合の計算例とグラフが含めてあるのでそちらもご参照ください)。
18人以上の顧客がある可能性はずいぶん低いようです。その確率は1−(17人までの累積確率)で求められるので、以下のようになります。
1.43%という確率は非常に小さいので、18人以上の顧客に対応するだけの店員数は必要なさそうです。この場合、17人までの顧客に対応できる店員数に少し人員を減らしてみる、といった判断が可能です。
実際には、業種にもよりますし(飲食店だともっと顧客数が多いでしょう)、より詳細な場合分け(晴天の場合と雨天の場合の客足の違いやイベント開催日への対応など)も必要になるでしょうが、ポアソン分布は、一定の割合で来客がある場合に(事象が定常的に発生すると想定されるときに)、余裕を持った対応のできる人員と人件費との最適な配分を決めるための目安として使えるでしょう。
今回は、まれにしか起こらない事象の確率分布としてポアソン分布を取り上げました。上で見た応用例の他にも、さまざまな分野で活用できそうですね。
次回は、試行を繰り返したときに、k回目に成功する確率(=成功するまでにk−1回失敗する確率)を求めるために使われる幾何分布と、n回成功するまでにk回失敗する確率を求めるために使われる負の二項分布を取り上げます。次回もお楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
ポアソン分布の確率質量関数や累積分布関数の値を求めるための関数
POISSON.DIST関数: ポアソン分布の確率質量関数や累積分布関数の値を求める
形式
POISSIN.DIST(イベント数, 平均, 関数形式)
引数
- イベント数: 目的の事象が起こる回数(kの値)を指定する。
- 平均: 目的の事象が一定期間(一定数)の中で起こる平均の回数を指定する。
- 関数形式: 以下の値を指定する。
- FALSE …… イベント数に対する確率質量関数の値を求める
- TRUE …… イベント数の成功数までの累積分布関数の値を求める
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.