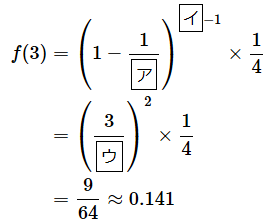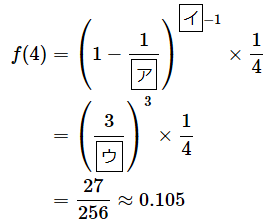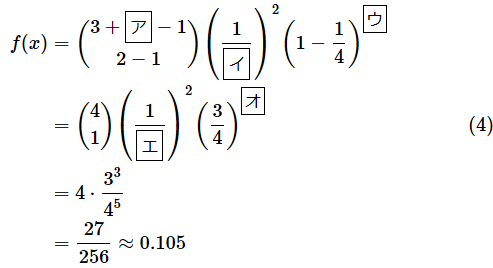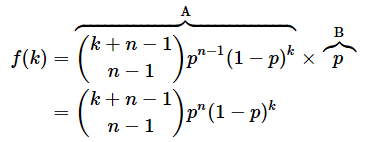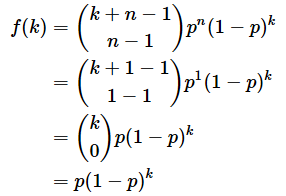[データ分析]幾何分布と負の二項分布 〜 三度目の正直の確率は?:やさしい確率分布
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載(確率分布編)の第5回。幾何分布とは、k回目に成功する確率の分布です。一方、負の二項分布は、n回成功するまでにk回失敗する確率の分布です。これらの確率分布が利用できる事例を確認した後、確率質量関数や累積分布関数の求め方、可視化の方法などを解説していきます。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』連載(記述統計と回帰分析編)の続編で、確率分布に焦点を当てています。
この確率分布編では、推測統計の基礎となるさまざまな確率分布の特徴や応用例を説明します。身近に使える表計算ソフト(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムでの作成例にも触れることにします。
数学などの前提知識は特に問いません。中学・高校の教科書レベルの数式が登場するかもしれませんが、必要に応じて説明を付け加えるのでご心配なく。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。趣味の献血は心拍数が基準を超えてしまい99回で中断。心肺機能を高めるために水泳を始めるも、一向に上達せず。また、リターンライダーとして何十年ぶりかに大型バイクにまたがるも、やはり体力不足を痛感。足腰を鍛えるために最近は四股を踏む日々。超安全運転なので、原付やチャリに抜かされることもしばしば(すり抜けキケン、制限速度守ってね!)。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の確率分布編、第5回です。前回は、まれにしか起こらない事象が起こる確率分布であるポアソン分布を取り上げました。今回は、k回目に成功する確率の分布である幾何分布と、n回成功するまでにk回失敗する確率の分布である負の二項分布を取り上げ、その意味や特徴などを見ていきます。
三度目の正直の確率を求めよう 〜 幾何分布
人気アーティストのライブに行きたくても、チケットが抽選でしか手に入らず、なかなかチャンスに恵まれないこともよくありますね。三度目の正直で、ようやくチケットが手に入ったという経験をお持ちの方も多いのではないでしょうか。
そこで、三度目の正直ならぬk度目の正直……つまり、k回目に当選する確率の分布について考えてみましょう。名前だけ先に出すと、この確率分布は幾何分布(Geometric distribution)と呼ばれます。図1は当選確率がp=1/4の場合に、ちょうどk=3回目に当選する確率を図解したものです。

図1 三度目の正直の(3回目に当選する)イメージ
3回目に当選するということは、2回は落選したということ。一般的に言うと、k回目に当選するということは、k−1回は落選したということ。k−1回落選する確率と1回当選する確率を掛ければk回目に当選する確率が求められる。
幾何分布は、前提として各試行が独立であることに注意してください。前回の結果が次回の結果に影響を及ぼすことはない、ということですね。
また、毎回の成功確率(ここでは当選確率)は一定であるものとします。成功確率をpとすると、失敗確率は1−pですね。
幾何分布と以前に説明した超幾何分布は名前は似ていますが、異なるものであることに注意してください。超幾何分布(例えば、くじ引き)では、試行が独立しておらず、前回の結果が次回の結果に影響を及ぼすため、成功確率が試行ごとに変化します。このような抽出の仕方を非復元抽出と呼びましたね。一方、幾何分布は復元抽出(試行が独立で、成功確率が一定)を前提としています。確率変数の値kに対する確率質量関数の値についても、超幾何分布は「k回成功する確率」ですが、幾何分布は「k回目に成功する確率」と、異なっています。
図1の説明からも分かるように、幾何分布ではk−1回がいずれも1−pの確率で失敗し、k回目に1回だけ確率pで成功するので、その確率質量関数は以下のように表されます。確率変数の値はkです。
この式は、図1のイメージから比較的素直に理解できると思います。(1)式に説明を加えると以下のようになります。
「成功」というのは必ずしもいい結果が得られるという意味ではなく、目的の事象が起こるということでしたね。製品の検査の例であれば、不良品が見つかることが目的の事象となるので、不良品の発見が「成功」ということになるかもしれません。
では、確認のためにライブチケットの当選確率pを1/4としたとき、k=3の場合(3回目に当選する確率)とk=4の場合(4回目に当選する確率)を(1)式に当てはめて求めてみましょう。オレンジ色の部分をクリックまたはタップすると答えが表示されます(以降も同様です)。
・k=3の場合(3回目に当選する場合:図1の場合)
答え: ア= 4 、イ= 3 、ウ= 4
・k=4の場合(4回目に当選する場合)
答え: ア= 4 、イ= 4 、ウ= 4
幾何分布の累積分布関数F(k)は、k回目までに成功する確率を表します。例えば、3回目までに成功する確率は、「1回目に成功する確率、2回目に成功する確率、3回目に成功する確率」の累計です。このように、順に値を足していっても求められますが、k回全てが失敗である確率を1から引いた値と等しくなるので、
で求めることができます。
ちょっと現実的な例で計算してみましょう。1等6億円のスポーツくじBIGでは、サッカーの試合の勝ち、負け、引き分けを14試合について全て当てなくてはいけないので、当選確率pは以下のようになります(勝ち、負け、引き分けが等確率であるとした場合)。
だいたい480万分の1ですね。では、このくじを1枚ずつ100回購入したときに、100回目までに1等が当選する確率はいくらでしょうか。これは累積分布関数の値なので、(2)式に当てはめると以下のようになります。
パーセント単位で表すと0.0021%です。1等の期待値(金額)は0.000021×600,000,000=12,600円です(キャリーオーバーがある場合。なければ、1等の当選金額は3億円が上限)。1枚300円なので、300×100=30,000円を払っても、期待できる見返りは12,600円にしかならないことが分かります(2等以下も考えるともう少し高くなります)。もちろん、あくまでも平均の話なので、幸運にも1等が当選することがあるかもしれません。実際には、筆者のように全てハズレという場合がほとんどですが、外れた分はスポーツ振興に役立てられているということですね。
幾何分布の確率質量関数と累積分布関数を可視化してみよう
BIGの例は確率があまりにも小さく、kの値を大きくしても可視化しづらいので、ライブチケットの例で可視化してみます。Excelには幾何分布の確率質量関数や累積分布関数の値を求める関数がありません。従って、(1)式と(2)式を使って計算します。作成の手順は図2の後に記しておきます。
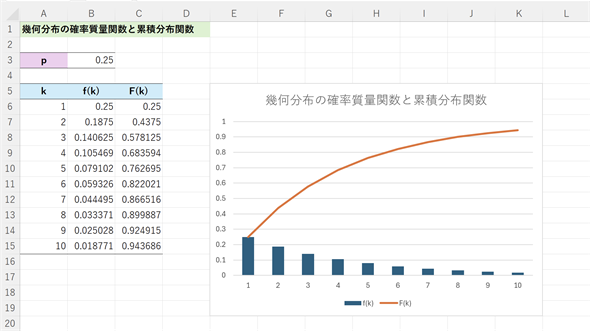
図2 幾何分布の確率質量関数と累積分布関数
Excelには幾何分布の確率質量関数と累積分布関数の値を求める関数がないので、(1)式と(2)式に従って計算する。ただし、次項で述べる負の二項分布の確率質量関数と累積分布関数の値を求める関数NEGBINOM.DIST関数で代用することはできる(後述)。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、[幾何分布]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。具体的な操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB6に=(1-B3)^(A6:A15-1)*B3と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルB6〜B15)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルC6に=1-(1-B3)^A6:A15と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルC6〜C15)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルB5〜C15を選択する
- [挿入]タブを開き、[複合グラフの挿入]ボタンをクリックして[集合縦棒 - 折れ線]を選択する
ここで示した事例は分かりやすさを優先した単純なものですが、幾何分布は、機械が何回の使用で故障するかの確率を求めたり、あるWebサイトにアクセスするユーザーが何回目の訪問で購買活動を行うかの確率を求めたりするのに使えます。
では、少し話題を変えて、次に負の二項分布を見てみましょう。
二匹目の泥鰌(どじょう)が得られるまでの確率を求めよう 〜 負の二項分布
本来、二匹目の泥鰌というのは、うまくいった人や物事のマネをして、うまく事を運ぼう(としてもうまくいかないものだ)という意味ですが、ここでは文字通り、複数回成功するまでの確率の話をします。もう少し正確に言うと、n回成功するまでにk回失敗する確率を求めます。毎回の試行は独立であるものとし、各試行での成功確率も一定であるものとします。こちらについても名前だけ先に出しておくと、負の二項分布(Negative binomial distribution)と呼ばれる確率分布を利用します。
文献によっては異なる文字を使って「k回成功するまでにx回失敗する確率」と表している場合(確率変数の値はx)や、成功と失敗を逆にして「r回失敗するまでにk回成功する確率」と表している場合(確率変数の値はk)などがあります。Excelのヘルプでは「r回成功するまでにx回失敗する確率」(確率変数の値はx)となっています。慣れないうちは混乱してしまいますが、以下で解説する負の二項分布の意味を理解していれば、どのように表現されていても適切に利用できるはずです。
図3のような例で考えてみましょう。またまたライブチケットの例です。チケットの抽選にn回当選するまでにk回落選する確率を求めます。この例では、n=2、k=1ですね。
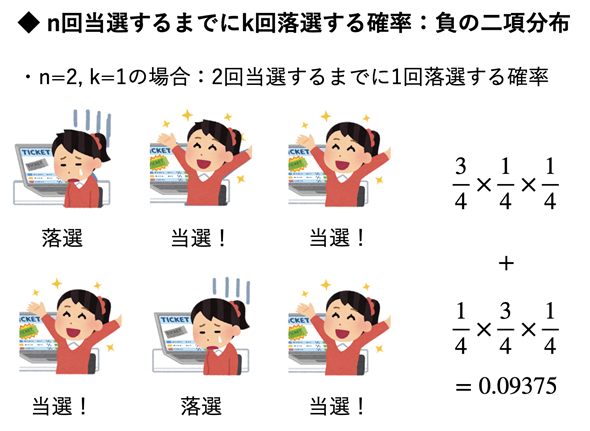
図3 n=2回当選するまでにk=1回落選する例
n=2回当選するまでにk=1回落選しているということは、「落選―当選―当選」と「当選―落選―当選」の場合。試行の最後は必ず当選であることに注目しよう。試行回数はn+kとなる。この例であれば2+1=3回。n回成功するまでにk+n回の試行を行う確率とも考えられる。
2回当選するまでに1回落選するのは図3に示した2つの場合があります。それらの確率を足したものが答えとなるわけですね。ここでは、2回当選する確率を求めているのではなく、2回当選するまでに1回失敗する確率を求めていることに注意が必要です。従って、「当選―当選―落選」は図3には含まれません(それを含めると、単に3回中2回当選する確率となり、二項分布で表されることになります)。
負の二項分布の確率質量関数f(k)は以下の通りです。ここでは、確率変数の値は失敗回数を表すkであるということに注意してください。
ちょっと複雑な式なので、この式の意味については後述することとして、まずは具体的な数値を当てはめて計算結果を確かめておきましょう。図3とは少し値を変えて試してみます。当選確率p=1/4として、2回当選するまでに3回落選する確率を求めましょう。この場合、n=2, k=3なので、以下のようになります。
答え: ア= 2 、イ= 4 、ウ= 3 、エ= 4 、オ= 3
(4)式の最初の、
は、4つの中から1つを選ぶ組み合わせ数(4C1=4)のことで、それ以降のかっこは単に分数を囲んだだけのものです。
では、確率質量関数の意味を見ていきます。図4をご覧ください。最後が必ず成功(当選)になっており、それ以前は二項分布であることに気付けば、上の式が簡単に導き出せます。最後に成功するBの確率はもちろんpです。それ以前の部分Aの試行数は全体の試行数k+nから1を引いたk+n−1ですね。その中でn−1回成功する確率なので、二項分布の式に試行数k+n−1、成功数n−1、失敗数kを当てはめれば求められます。
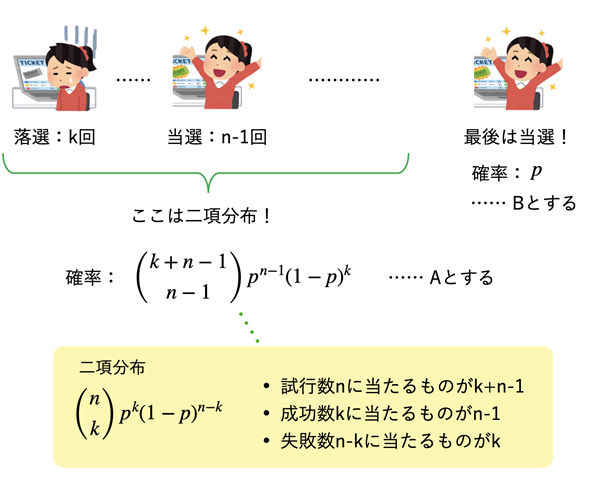
図4 負の二項分布は、成功する直前までが二項分布になっている
n回成功(当選)、k回失敗(落選)なので、全体の試行数はn+k回となる。最後の1回は必ず成功(確率はp)となり、その前までのn+k−1回は、n−1回が成功で、k回が失敗となる二項分布。図のAとBを掛ければ負の二項分布の確率質量関数の値が求められる。
f(k)は、図4のAとBとの積で求められるので、以下のようになります。上に示した(3)式と一致していることを確認しておいてください。
なお、n=1の場合はk回の失敗の後、k+1回目に1回だけ成功することになります。ということは、n=1の場合の負の二項分布のf(k)は、幾何分布のf(k+1)と等しくなることが分かります。
◆ 負の二項分布でn=1の場合
◆ 幾何分布
このことについては、次項でNEGBINOM.DIST関数について解説した後、またお話しします。
負の二項分布の累積分布関数は、n回成功するまでにk回以下失敗する確率です。これについては次の項で具体的に見ることにしましょう。
負の二項分布の確率質量関数と累積分布関数を可視化してみよう
こちらもライブのチケットの例で可視化してみます。当選確率p=1/4のとき、n=2回当選するまでに、k回落選する確率を求めます。負の二項分布については、ExcelのNEGBINOM.DIST関数を使って確率質量関数や累積分布関数の値を求めることができます。従って(3)式を使わなくても簡単に値が求められます。
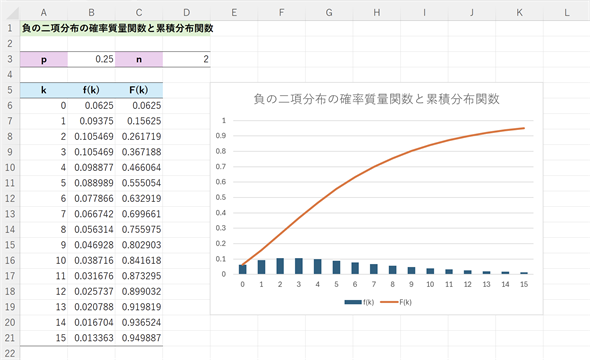
図5 負の二項分布の確率質量関数と累積分布関数
確率質量関数と累積分布関数の値は(3)式に従って計算してもよいが、いずれもNEGBINOM.DIST関数で求められる。確率質量関数と累積分布関数の意味についても確認しておこう。例えばk=5のときの確率質量関数の値は2回当選するまでにちょうど5回落選する確率となっており、累積分布関数の値は2回当選するまでに、5回まで(0〜5回)落選する確率となっている。
グラフ作成の手順は以下の通りです。サンプルファイルをこちらからダウンロードし、[負の二項分布]ワークシートを開いて試してみてください。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。具体的な操作方法は、サンプルファイル内に記載しています。なお、GoogleスプレッドシートのNEGBINOM.DIST関数には最後の引数がない(確率質量関数の値しか求められない)ことに注意が必要です。具体的な操作方法は、サンプルファイル内に記載しています。
◆ Excelでの操作方法
- セルB6に=NEGBINOM.DIST(A6:A21,D3,B3,FALSE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルB6〜B21)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルC6に=NEGBINOM.DIST(A6:A21,D3,B3,TRUE)と入力する
- 古いバージョンのExcelでスピル機能が使えない場合は、あらかじめ結果が求められるセル範囲(セルC6〜C21)を選択しておき、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押す
- セルB5〜C21を選択する
- [挿入]タブを開き、[複合グラフの挿入]ボタンをクリックして[集合縦棒 - 折れ線]を選択する
- [グラフのデザイン]タブを開き、[データの選択]ボタンをクリックする
- [データソースの選択]ダイアログボックスで[横(項目)軸ラベル]の下の[編集]ボタンをクリックする
- [軸ラベル]ダイアログボックスで[軸ラベルの範囲]ボックスをクリックし、セルA6〜A21を選択する
- [OK]をクリックして[軸ラベル]ダイアログボックスを閉じる
- [OK]をクリックして[データソースの選択]ダイアログボックスを閉じる
NEGBINOM.DIST関数の引数は図6のように指定します。
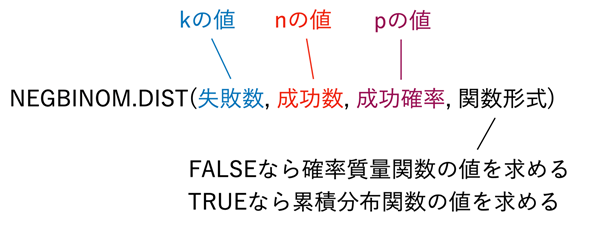
図6 NEGBINOM.DIST関数に指定する引数
図5の例では、失敗数として、セルA6:A21というセル範囲を指定しているので、スピル機能によりセルA6〜A21の失敗数に対する確率質量関数の値や累積分布関数の値が一度に求められる。つまり、n回成功するまでにk回失敗する確率や累積確率が求められる。
Excelには幾何分布の確率質量関数や累積分布関数の値を求める関数はありませんが、負の二項分布の確率質量関数や累積分布関数の値を求めるNEGBINOM.DIST関数で代用できます。すでに述べた通り、成功数n=1のとき、負の二項分布のf(k)は、幾何分布のf(k+1)と等しくなります。従って、幾何分布のf(k)を求めたいときには、NEGBINOM.DIST関数の成功数に1を指定し、失敗数にk-1の値を指定すれば答えが得られます。サンプルファイルにはそれらの計算を比較した例も含めてあるので、ぜひ参照してみてください。
負の二項分布のちょっとした応用例 〜 大谷選手は何打席までに50本のホームランを打つのか
この執筆を執筆している時点では、ドジャースの大谷翔平選手は今シーズン375打席中、26本のホームランを放っています。そこで、この調子が維持されるものとして、負の二項分布を利用し、50本目のホームランを打つまでの打席数とその確率を求めてみましょう。単純に考えると、ほぼ倍のホームラン数なので、375×2=750打席ぐらいで達成できそうな気がしますが、さてどうでしょうか。1打席でホームランを打つ確率は、これまでの成績を基に26/375とします。
750打席目に50本目のホームランを打つということは、成功数n=50、失敗数k=700と考えられます。従って、750打席目までに50本目のホームランを打つ確率は、負の二項分布の累積分布関数=NEGBINOM.DIST(700, 50, 26/375, TRUE)で求められます。実際に計算してみると0.634となります。倍の打席数だからといってほぼ確実というわけではなさそうですね。
図7はk=500〜860までとし、NEGBINOM.DIST関数で求めた累積分布関数の値とそれをグラフにしたものです。この例もサンプルファイルに含めてあるので、ぜひご参照ください。作成方法は図5とほとんど同じです。
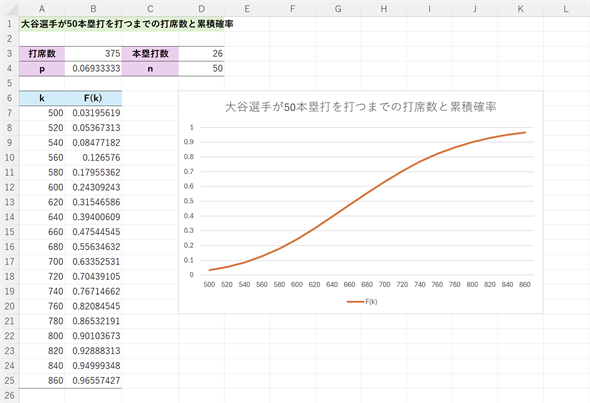
図7 大谷選手が50本目のホームランを打つまでの打席数とその確率
nは成功数(ホームランの数)、kは失敗数(ホームラン以外の打席数)。ホームランの確率はセルB4に=D3/B3と入力されているので、セルB7に=NEGBINOM.DIST(A7:A25,D4, B4, TRUE)と入力すれば、それぞれのkに対する累積分布関数の値が求められる。なお、スピル機能が使えないバージョンのExcelであれば、結果が正しく表示されないが、その場合はセルB7〜B25を選択し、関数を入力した後、入力の終了時に[Ctrl]+[Shift]+[Enter]キーを押せば配列数式として入力され、結果が表示される。
今回は、親しみやすさ重視で宝くじやスポーツの事例を取り上げて解説しましたが、負の二項分布は、n個の不良品が出るまでにk個の良品が製造される確率を求めたり、n回の購買活動が行われるまでにWebサイトにk回アクセスされる確率を求めたりするのにも使われます。他にもさまざまな分野で活用できそうですね。
今回で、離散型確率分布のお話はひと区切りです。連続型確率分布のお話に移りたいと思いますが、さらなる応用のために、番外編として、累積分布関数の逆関数のお話を挟んでおきたいと思います。例えば、図7の例であれば、累積確率が95%以上となるkの値(それまでのホームラン以外の打席数)を求めることができます。ちなみに答えは841打席です(もっとも、メジャーリーグの全試合は約160試合なので、全ての試合で4回の打席に立ったとしても640打席しかありません。もちろんムリだということではなく、95%の確率でほぼ確実にというのが難しいということです。2024年9月20日追記:現地時間2024年9月19日に50本塁打を達成しました!)。というわけで、次回の番外編もお楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、今回取り上げた関数の基本的な機能と引数の指定方法だけを示しておきます。
負の二項分布の確率質量関数や累積分布関数の値を求めるための関数
NEGBINOM.DIST関数: 負の二項分布の確率質量関数や累積分布関数の値を求める
形式
NEGBINOM.DIST(失敗数, 成功数, 成功確率, 関数形式)
引数
- 失敗数: 目的の事象が起こらない回数(kの値)を指定する。
- 成功数: 目的の事象が起こる回数(nの値)を指定する。
- 成功確率: 1回の試行で目的の事象が起こる確率を指定する。
- 関数形式: 以下の値を指定する。
- FALSE …… 失敗数に対する確率質量関数の値を求める
- TRUE …… 失敗数までの累積分布関数の値を求める
「やさしい確率分布」
Copyright© Digital Advantage Corp. All Rights Reserved.