 |
基礎技術解説:秘密分散法
注目の情報管理方式「しきい値秘密分散法」
岩本 琢哉 (Takuya Iwamoto)株式会社シーフォーテクノロジー
2004/11/27
| しきい値秘密分散法 |
しきい値秘密分散法の具体的な方式にはいくつかありますが、RSA暗号の開発者の1人であり現イスラエル ワイツマン研究所教授であるAdi Shamir氏が発表した方式が最も有名です。これはk-out-of-n分散方式といい、「分割させる数 : n 」と、「復元に必要な数(しきい値): k 」が異なる方式です。ちなみに、前節で述べたn-out-of-n分散方式は分割数としきい値が等しい方式です(「秘密分散」といえば、一般的にk-out-of-n分散方式のことを指します。ここではほかと区別しやすいように「しきい値秘密分散法」という言葉を使っています)。
さて、分割数としきい値が異なると何がよいのでしょうか? それは冗長性を持たせることが可能になるという点です。例として2-out-of-3の場合を説明します(パラメータは k ≦ n を満たせば好きに設定できます)。この場合、守りたい情報を3つに分け、そのうち任意の2つが集まれば復元することができる、ということになります。
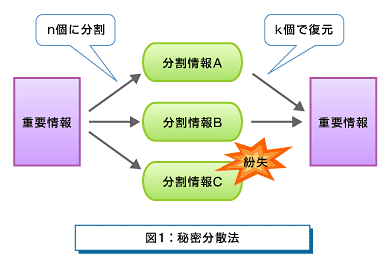
詳しくは次節で説明しますが、個々の分割情報は元の鍵情報とは相関性のない情報になっています。 そのため、紛失した情報を第三者に拾われても、そこから元の鍵情報が漏えいすることはありません(厳密には暗号化ではなく符号化なのですが、秘匿するという機能においては同じです)。このように、不正利用も2人の分割情報保持者が結託しない限り不可能です。つまり、機密性を確保することができています。また仮に、1つの分割情報が紛失しても、しきい値分の分割情報(この場合は2つ)が残っていれば復元することができます。つまり、可用性をも確保することができています。
この、機密性と可用性を同時に満たせるところが、暗号とは最も異なる部分であり、しきい値秘密分散法の最大のメリットといえます。今回は2-out-of-3を例に挙げましたが、これらのパラメータは自由に設定することができます。例えば、6-out-of-10のように設定すると、多数決のような機能が実現できます。
| 安全性 |
次にしきい値秘密分散法の安全性について説明します。安全性については、この方式の仕組みを理解していただければ一目瞭然(りょうぜん)ですので、以下で仕組みを具体的に説明します。
この方式のベースとなっている技術はなんと、皆さんが中学校で習った連立方程式です。数学が苦手という方も、ちょっと頑張って読んでいただければ、目からウロコだと思います。先に概要だけを述べますと、連立方程式において未知数を求めるためには、未知数の個数だけ関係式が必要となります。そこで、分割情報によってその個数分の関係式を作ってあげましょうというものです。
それでは、具体的に例を挙げて説明します。 前節同様に2-out-of-3の場合で、分割処理から説明します。守りたい秘密情報をSとします。これは何らかの方法で数値に変換しておきます(暗号でもデータをすべて数値に置き換えて計算しています)。図2のように、x-y直交座標系でSをy切片とするような直線L : y = ax + Sを適当に引きます。

次にこの直線上の点を重複しないように3つ取ります。ここでは3つの点をA、B、C とします。実はこの3つの座標情報が分割情報そのものになります。あとは直線Lの情報を消去し、分割情報A、B、Cをそれぞれの管理者に持たせておきます。
そして復元処理です。しきい値は2ですので、2個の分割情報が集まれば復元できることになります。まず、1つだけ分割情報が得られたとします。
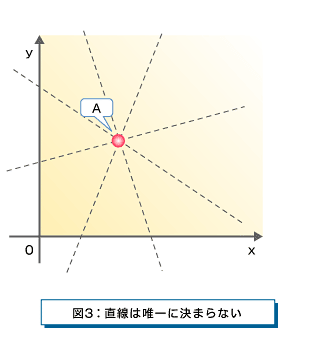
1つの分割情報から分かることは、1つの点の座標です。この座標を通る直線は無限にあり、これだけでは元の直線(と思われるもの)を選択することはできません(図3)。
しかし、もう1つの分割情報があれば、別の1点の座標が判明しますから、この2点を通る直線が唯一に決まります(図4)。あとはこの直線のy切片を求めればSを復元できたことになります。
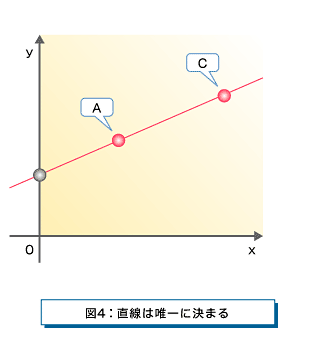
分割情報はただの座標情報ですので、元の秘密情報Sとは直線以外の関係を持たないことになります。ですから、しきい値分の分割情報が分からず、直線が決定しない限り、分割情報から、元の秘密情報Sは類推できないことになります。このように、仕掛けは非常に単純で安全性の証明も可能です。ですが、単純なだけに、セキュリティと機能のバランスが絶妙に取れた非常に効率のよい方式になっています。
ちなみに、直線を求めるのは2-out-of-3の場合です。6-out-of-10の場合は、y = ax5 + bx4 + cx3 + dx2 + ex + Sといった5次連立方程式を使った曲線を求めることになります。
| 【注】 証明されているのは情報量的安全性です。情報量的安全性とは、無限の計算能力を持つ攻撃者でも、情報量の不足により攻撃が成功しえないことを言います。 |
| 秘密分散法の利用法 |
最後に、秘密分散法が実際にどのように使われているのかを説明します。実はしきい値秘密分散法が発表されたのは1979年で、特に新しい技術ではありません。PKI(Public Key Infrastructure)ではSecret Shareと呼ばれる当たり前の技術で、CA(Certificate Authority)の秘密鍵のような非常に機密性の高い情報に対して利用されています。また、有名な暗号ソフトであるPGP(Pretty Good Privacy)でも Key splitting という名で使用されています。
秘密分散についての認識ですが、国際的に見て日本の対応は遅れています。米国などでは、政府が暗号の鍵の管理法として、暗号化または秘密分散のどちらかを義務付けています。米国の政府機関で使われる暗号装置では鍵を出力する際に暗号化または秘密分散のどちらかを使うものが多くあり、秘密分散が採用されている製品も少なくありません。
このように、従来は基本的に鍵に対して使われる技術でしたが、近年ではISMSなどの企業の情報管理を見直す流れがあってか、鍵以外のデータに対しても使用されるようになっており、ディザスタリカバリ(災害時復旧)の1方式としても注目されています。また、分割情報の正当性を検証することにより、認証に利用しようとする動きもあります。
今回は、機能の違いを明確にするために暗号と比較して説明しましたが、暗号が、秘密分散法に比べて劣っているわけではありません。セキュリティの評価は機密性と可用性のみから判断されるのではなく、さまざまな視点があってしかるべきでしょう。そのような視点を理解し、おのおのの特性を見極め、状況に応じてこれらを使い分けることが重要となります。
2/2 |
| Index | |
| 注目の情報管理方式「しきい値秘密分散法」 | |
| Page1 暗号化 鍵の管理方法 リスク分散 |
|
| Page2 しきい値秘密分散法 安全性 秘密分散法の利用法 |
|
| Security&Trust記事一覧 |
- Windows起動前後にデバイスを守る工夫、ルートキットを防ぐ (2017/7/24)
Windows 10が備える多彩なセキュリティ対策機能を丸ごと理解するには、5つのスタックに分けて順に押さえていくことが早道だ。連載第1回は、Windows起動前の「デバイスの保護」とHyper-Vを用いたセキュリティ構成について紹介する。 - WannaCryがホンダやマクドにも。中学3年生が作ったランサムウェアの正体も話題に (2017/7/11)
2017年6月のセキュリティクラスタでは、「WannaCry」の残り火にやられたホンダや亜種に感染したマクドナルドに注目が集まった他、ランサムウェアを作成して配布した中学3年生、ランサムウェアに降伏してしまった韓国のホスティング企業など、5月に引き続きランサムウェアの話題が席巻していました。 - Recruit-CSIRTがマルウェアの「培養」用に内製した動的解析環境、その目的と工夫とは (2017/7/10)
代表的なマルウェア解析方法を紹介し、自社のみに影響があるマルウェアを「培養」するために構築した動的解析環境について解説する - 侵入されることを前提に考える――内部対策はログ管理から (2017/7/5)
人員リソースや予算の限られた中堅・中小企業にとって、大企業で導入されがちな、過剰に高機能で管理負荷の高いセキュリティ対策を施すのは現実的ではない。本連載では、中堅・中小企業が目指すべきセキュリティ対策の“現実解“を、特に標的型攻撃(APT:Advanced Persistent Threat)対策の観点から考える。
|
|




