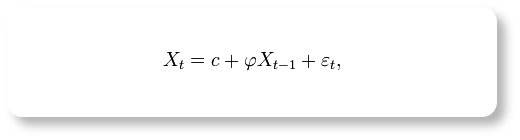時系列分析Ｉ ――ARMAモデルと時系列分析：ITエンジニアのためのデータサイエンティスト養成講座（9）（2/4 ページ）

システムログも金融取引データも時系列で分析できる。ビジネスシーンで求められるデータ分析の多くを占める「時系列データ」分析の基礎を解説。

[中林紀彦，日本アイ・ビー・エム]

自己回帰 AR(p) モデル

　例えば、株価など時系列（日次）で変化する事象を表すデータで、今日の株価は1日前の株価の値と相関関係があり、式1のように表すことができるモデルをAR(1)過程と呼びます。

　1日前と2日前の2世代前までのデータと相関性がある場合にはAR(2)過程ということができ、p日前までのデータと相関性がある場合にはAR(p)過程と呼びます。

式1（Wikipedia日本語版「自己回帰移動平均モデル」から引用）

　式1を見ると分かりますが、AR(1)過程の性質はパラメーターφによって決定されます。

　ここではφの値をいろいろと変化させてサンプルデータを生成し、AR(1)過程の特徴を見ていきましょう。

自己回帰モデルはパラメーターが変わるとどうなる？（1）： φ＝1.01の場合

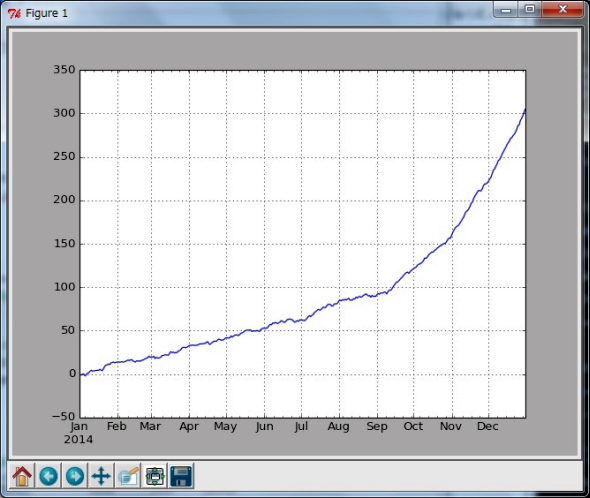
　まずは必要なライブラリを読み込んで（In [1]〜In [5]）、365日の時系列インデックスを生成します（In [6]〜In [9]）。パラメーターに1.01を指定してサンプルデータを生成しプロットします（In [10]〜In [15]）。図1のようにφ＝1.01の場合には前日の値より1%増加するということなので、ノイズが含まれているため、少しまばらではありますが、単調に増加していくことが分かります。

In [1]: # 必要なライブラリの読み込み
In [2]: %pylab
Using matplotlib backend: TkAgg
Populating the interactive namespace from numpy and matplotlib
In [3]: import pandas as pd
In [4]: import statsmodels.api as sm
In [5]: from statsmodels.tsa.arima_process import arma_generate_sample
In [6]: # 期間の設定：365日
In [7]: nobs = 365
In [8]: # 時系列インデックスの生成
In [9]: dates = pd.date_range(start='2014-01-01', periods=nobs)
In [10]: # MAパラメーターを設定：今回はARモデルなのでMA(0)とします
In [11]: maparams = np.array([1])
In [12]: # φ=1.01としてサンプルデータを生成しグラフにプロット
In [13]: arparams = np.array([1, -1.01])
In [14]: y1 = pd.TimeSeries(arma_generate_sample(arparams, maparams, nobs), index=dates)
In [15]: y1.plot()
Out[15]: <matplotlib.axes.AxesSubplot at 0x6fb30b0>

図1　φ＝1.01の場合の出力結果

自己回帰モデルはパラメーターが変わるとどうなる？（2）：φ＝0.5の場合

　次に0.5の場合を見てみましょう（In [16]〜In [23]。

In [16]: # 前のグラフを閉じる
In [17]: plt.close()
In [18]: # φ=0.5としてサンプルデータを生成しグラフにプロット
In [19]: arparams = np.array([1, -0.5])
In [20]: y2 = pd.TimeSeries(arma_generate_sample(arparams, maparams, nobs), index=dates)
In [21]: y2.plot()
Out[21]: <matplotlib.axes.AxesSubplot at 0x71a6ed0>
In [22]: #
In [23]: plt.close()

図2　φ＝0.5の場合

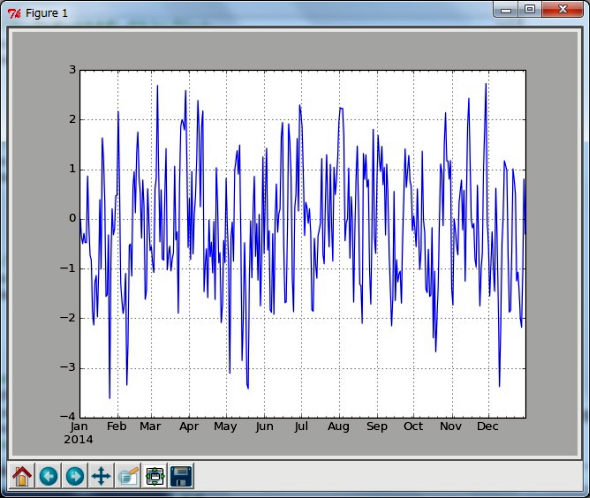
　（1）と同様にグラフを描くと図2のようになり、パラメーターの絶対値が1以下のため、ノイズの影響で直線にはなりませんが、0近傍で値が定常になっていると見なせます。

自己回帰モデルはパラメーターが変わるとどうなる？（3）：φ＝−1.01の場合

　次にパラメーターが負（マイナス）のケースを見てみましょう（In [24]〜In [27]）。

In [22]: # 前のグラフを閉じる
In [23]: plt.close()
In [24]: # φ=-1.01としてサンプルデータを生成しグラフにプロット
In [25]: arparams = np.array([1, 1.01])
In [26]: y3 = pd.TimeSeries(arma_generate_sample(arparams, maparams, nobs), index=dates)
In [27]: y3.plot()
Out[27]: <matplotlib.axes.AxesSubplot at 0x795cad0>

図3　φ＝−1.01の場合

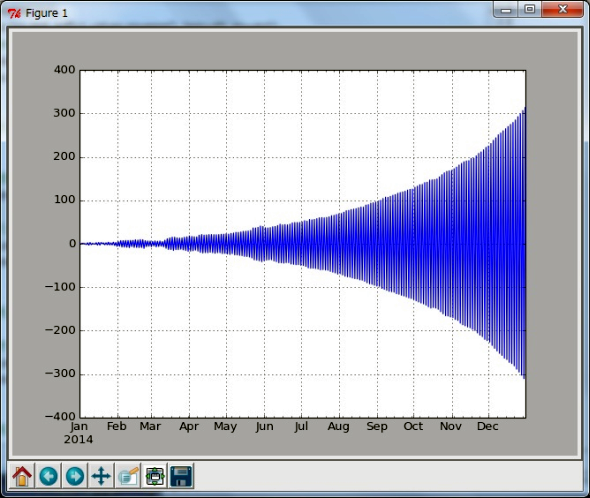
　図3を見ると、前日の値と正負の符号を変えながら発散していく様子が分かります。

　（1）から（3）のようにパラメーターφの値によって値の性質が大きく変化することがお分かりいただけたと思います。この知見は観測値からモデルを予測する際にも利用できますので、他にもいろいろなパラメーターを試してみてください。