鍵が漏れることも想定せよ――クラウド時代における「楕円曲線暗号」の必然性：クラウド時代の暗号化技術論（3）（2/3 ページ）

エンジニアであれば、楕円曲線を暗号に用いる「楕円曲線暗号」という言葉を聞いたことがあるでしょう。今回は楕円曲線暗号の仕組み、そしていまこの手法が注目されている理由を解説します。

[光成滋生，＠IT]

トーラスとは

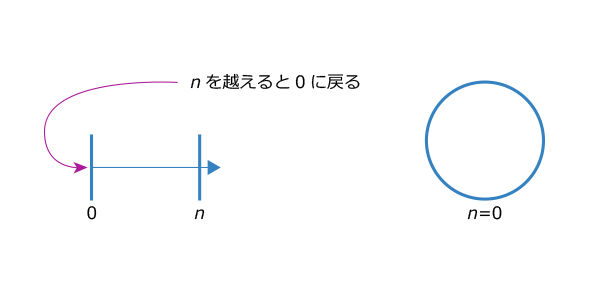
　RSA暗号やElGamal暗号は、ある決まった自然数nで割った余りの中で計算していました。nになると0に戻るので、一本の[0,n]という線分の両端を張り合わせて円周の上を動いていると見立てられます。

図2　0とnをくっつけると円周になる

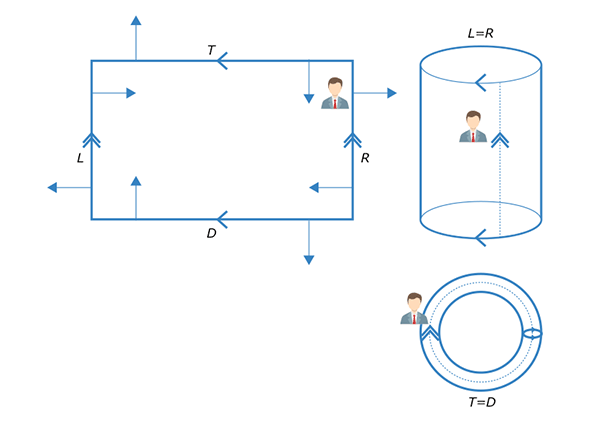
　これを2次元にすることを考えてみます。線分の代わりに長方形を考えましょう。その長方形の上を歩き回ることを考えます。右端に到達すると左端から出てきて、上端に到達すると下端から出てきます。昔はやったロールプレイングゲームを思い出す方もいらっしゃるかもしれませんね。

　1次元の場合と同じように、両端を張り付けてみます。長方形の左右の辺L、Rが同じなのですからそれらを張り合わせます。上下の辺T、Dも張り合わせます。するとひねったり伸ばしたりする必要はありますが、浮輪の表面のような形になります。

図3　トーラスのイメージ

　浮輪の表面をトーラスといい、その上で足し算を考えたものが「楕円曲線」です。小、中学校で習うつぶれた円を差す楕円とは異なり、“楕円曲線”という一つの用語ですのでご注意ください。

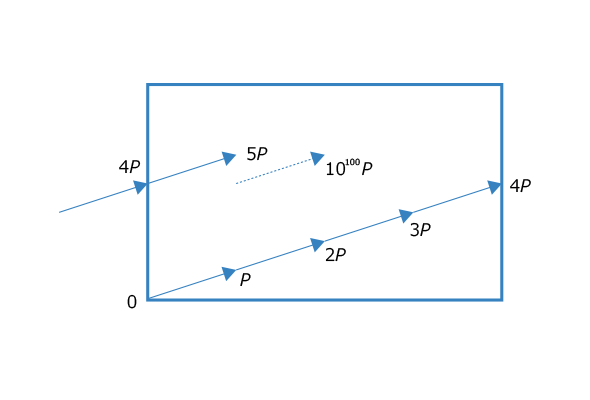
　楕円曲線上でゲームのキャラクターが歩き回ることを考えましょう。キャラクターの一歩がPだとします。原点Oから2歩進むと2Pの位置にいます。どんどん進んで端に到達すると逆から出てきます。10歩でも100歩でも10¹⁰⁰歩でも進めます。そして歩いて到達した位置10Pや100P、10¹⁰⁰Pは容易に求められることが知られています。

図4　楕円曲線上を歩く

　さて、移動していたキャラクターはうっかり何歩進んでいたか忘れてしまいました。ところが「今、自分がいる場所に何歩で到達できるのか」を求めることはとても難しいということが知られています。正確に書くと「点PとQが与えられたときに、Q=nPとなるnを求めよ」という問題になります。

　この問題を「楕円離散対数問題」（ECDLP）といいます。楕円曲線暗号はECDLPが難しいという仮定の下で作られています。

楕円曲線鍵共有

　楕円曲線を使った鍵共有を紹介します。冒頭で紹介したPFSで使われている手法です。

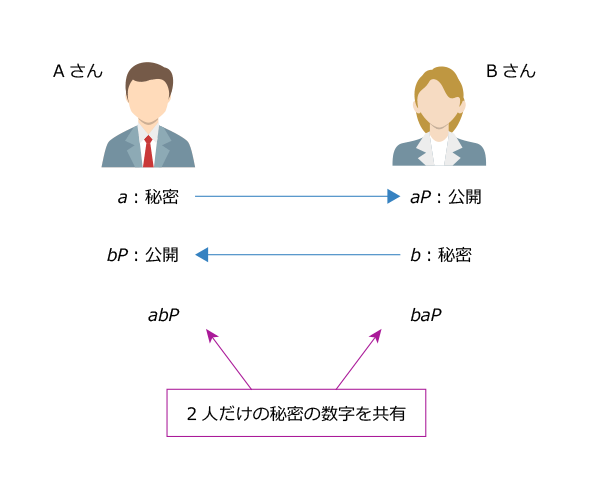
　AさんとBさんが鍵共有をしたい場合、それぞれが楕円曲線上の点Pを決めて固定します。Aさん、Bさんそれぞれが秘密の数字a、bをランダムに決めて、aP、bPを相手に渡します。ECDLPが困難なので、aP、bPが盗聴されてもa、bを求めることはできません。

• AさんはBさんからもらったbPをa倍　→　a(bP)=abP
• BさんはAさんからもらったaPをb倍　→　b(aP)=baP

　楕円曲線上でabP=baPなので、この数値を二人で秘密に共有できます。公開情報P、aP、bPからabPを求めることは困難であると信じられています。

　こうして得られたabPを、AESなどの共通鍵暗号の秘密鍵として使って通信を暗号化するのです。

図5　楕円曲線鍵共有