【Excelで学ぶデータ分析】うどん・そばの好みは出身地域で差があるか?(独立性の検定):やさしい推測統計(仮説検定編)
初歩から応用までステップアップしながら学んでいく『やさしいデータ分析』シリーズ(仮説検定編)の第7回。今回は、2つのカテゴリが独立であるか(=関連がないか/あるか)を調べる方法について解説します。
連載:
この連載は、データをさまざまな角度から分析し、その背後にある有益な情報を取り出す方法を学ぶ『社会人1年生から学ぶ、やさしいデータ分析』シリーズの「記述統計と回帰分析編」「確率分布編」「推測統計(区間推定編)」に続く「推測統計(仮説検定編)」です。
この連載では、観測されたデータを基に、平均に差があるかどうか、分散に差があるかどうかなどを吟味するために、仮説検定を行う方法や適用時の留意点などを説明します。身近に使える表計算ソフトウェア(Microsoft ExcelやGoogleスプレッドシート)を使いながら具体的に事例を見ていきます。
必要に応じて、Pythonのプログラムなどでの作成例にも触れることにしますが、数学などの前提知識は特に問いません。肩の力を抜いてぜひとも気楽に読み進めてください。
筆者紹介: IT系ライターの傍ら、これまで非常勤講師として東大で情報・プログラミング関連の授業を、一橋大でAI関連の授業を担当。かなり前から髪をブリーチしていて金髪先生を自称していたのだけれど、放置しているといい感じのグレーヘアーになってきたので、もはや寄る年波かと思う昨今。最近、成長したなと感じていることは、生まれてこの方どうしても食べられなかった納豆が食べられるようになったこと。唐揚げにはレモンをかけない派。
データ分析の初歩から応用まで少しずつステップアップしながら学んでいく連載の推測統計(仮説検定編)、第7回です。前回は、番外編として、G*Powerという便利なツールを使って検定に必要なサンプルサイズを求める方法を紹介しました。今回は独立性の検定と呼ばれる検定を取り上げます。例えば、出身地域と麺類の好みは独立している(=出身知識と麺類の好みには関係がない=出身地域によって麺類の好みに違いはない)か、そうでないかを検定します。この検定は一般にカイ二乗検定と呼ばれます。
独立性の検定についての基本的な考え方
「独立性」という言葉はちょっとつかみどころがなく、具体的な意味が分かりにくいですが、要するに「関係がない」ということです。今回は、上でも述べたように、出身地域と麺類の好みは独立しているかどうかを調べます。
一般的なイメージとして、関西人は「うどん」が、関東人は「そば」が好みだと思われているようです。そこで、実際にそうであるかどうかを調べてみようというわけです。といっても、ここで使うデータは架空のデータです。麺類にはラーメンなどもありますが、話を簡単にするために、うどんとそばに限って見ていきます(図1)。
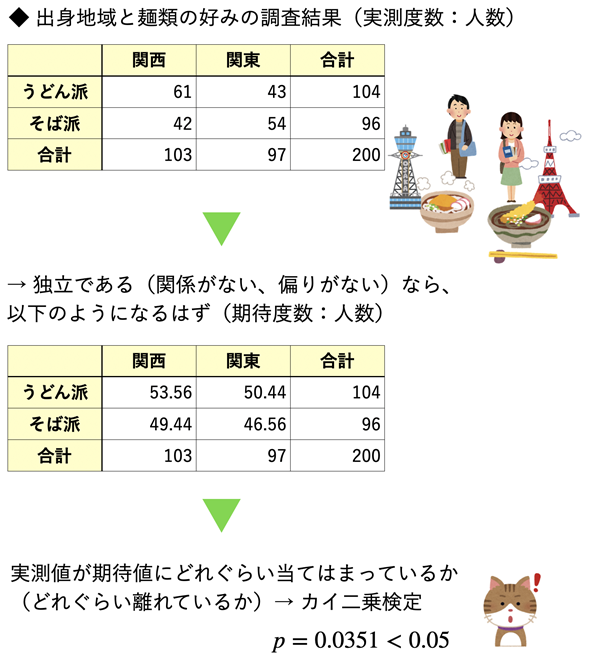
図1 出身地域によって麺類の好みに違いはあるか?
関西出身者と関東出身者に、うどんとそばのどちらが好みかを聞いたところ、上の表のような結果になった(実測度数)。もし、出身地域によって好みに違いがないのであれば、下の表のような値になるはず(期待度数)。実測度数が期待度数からどれぐらい離れているかを求めれば、出身地域と麺類の好みが独立であるかどうかが分かるはず。期待度数の求め方は後述する。
うどん文化とそば文化に関するウェザーニュースの記事などを見ると、地域による違いは、上の架空データよりもかなり如実に表れるようです。
独立性の検定では、実測度数と期待度数の差(の2乗)を基に、検定統計量χ2の値を求め、カイ二乗分布の累積分布関数からP値を求めます。しかし、そのような計算を行わなくても、CHISQ.TEST関数に実測度数と期待度数を指定すれば簡単にP値が求められます。
帰無仮説と対立仮説の確認から始めましょう。
- 帰無仮説(H0): 出身地域と麺類の好みは独立である
- 対立仮説(H1): 出身地域と麺類の好みは独立ではない
実測度数と期待度数の乖離(かいり)が大きいことを確かめたいので、片側検定となります。では、期待度数を求め、続いてCHISQ.TEST関数を使ってP値を求めてみましょう。
独立性の検定を行ってみよう
こちらからダウンロードしたExcelファイルを開いて試してみてください。[独立性の検定]ワークシートを表示して、図2のように操作します。Googleスプレッドシートのサンプルはこちらから開くことができます。メニューから[ファイル]−[コピーを作成]を選択し、Googleドライブにコピーしてお使いください。
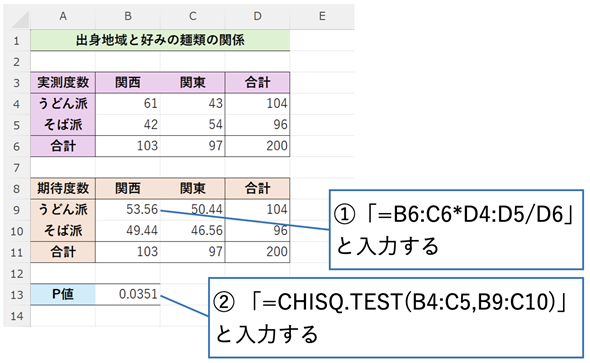
図2 期待度数を求め、独立性の検定(カイ二乗検定)を行う
セルB9に入力した=B6:C6*D4:D5/D6という式で全ての期待度数が求められるが、ちょっと意味が分かりにくいかもしれない。先頭のセル参照だけを取り出した=B6*D4/D6という式で考えると分かりやすい。「関西人」は103人(セルB6)いるが、うどん派とそば派の割合に偏りがないとすると(全体の比と同じであるとすると)、関西人のうどん派の数は104/200(セルD4/D6)という全体の割合と同じになるはず。従って、期待度数は=B6*D4/D6という式で求められる。ほかのセルも同様。期待度数が求められれば、後はCHISQ.TEST関数に実測度数の範囲と期待度数の範囲を指定するだけ。
Google スプレッドシートの場合、セルB9には「=ARRAYFORMULA(B6:C6*D4:D5/D6)」と入力します。ただ、Excelのスピル機能やGoogleスプレッドシートのARRAYFORMULA関数を利用して期待度数を一気に求める方法は少し分かりにくいかもしれません。各セルに入力すべき式を全て挙げてみると以下のようになります。
- セルB9 :=B6*D4/D6
- セルB10:=B6*D5/D6
- セルC9 :=C6*D4/D6
- セルC10:=C6*D5/D6
絶対参照と相対参照の組み合わせに慣れている方であれば、セルB9に=B$6*$D4/$D$6と入力し、セルB10、セルC9、セルC10にコピーしても同じ結果が得られます。なお、サンプルファイルでは、縦横の合計を求めるためのSUM関数は既に入力してあります(以降の例でも同様です)。
結果はP=0.0351 < 0.05なので、帰無仮説を棄却し、対立仮説の「出身地域と麺類の好みは独立ではない」を採用します。出身地域によって麺類の好みが異なることが統計的にも確認できました(5%有意)。今回のデータでは(といっても架空データですが)、関西では「うどん派」がやや多く、関東では「そば派」がやや多いと言えそうです。
なお、今回の例では2行2列の表を使いましたが、行数や列数が増えても考え方は同じです。
このようなデータを分析する際には、全体の関係と個々の関係に矛盾が生じるシンプソンのパラドックスに留意する必要があります。シンプソンのパラドックスとして有名なものに、カリフォルニア大学バークレー校での大学院合格率の例があります。全体では女性の合格率が男性よりも低かったが、個々の学科では女性の合格率が高かったというものです(男性の方が合格率の高い学科を志望する人数が多く、女性の方が難関学科を志望する人数が多かったため)。
検定統計量χ2とカイ二乗分布の累積分布関数によって検定を行うには
CHISQ.TEST関数を使わずに、定義通りに計算する方法も見ておきましょう。検定統計量は以下の式で求められます。
実測度数と期待度数の差の二乗が、期待度数に対してどの程度であるか、という値を合計したものですね。分散の計算に似た計算であることも分かると思います。
このようにして求めた検定統計量χ2に対する、カイ二乗分布の右側確率を求めます(これがP値となります)。右側確率はCHISQ.DIST.RT関数で求められます。自由度は(データの行数−1)×(データの列数−1)とします。この例では2行2列なので、自由度は(2−1)×(2−1)=1となります。サンプルファイルの[独立性の検定 (定義通りに計算)]ワークシートを開いて試してみてください(図3)。
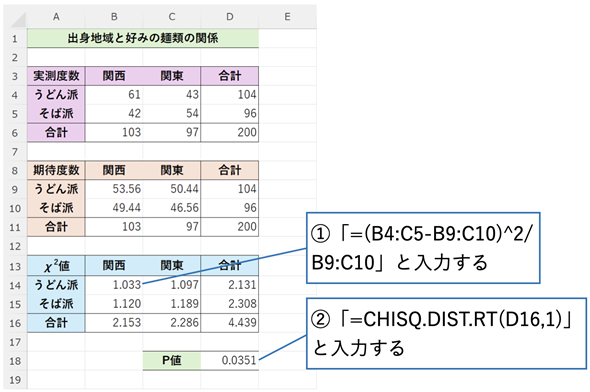
図3 定義に従って独立性の検定(カイ二乗検定)を行う
期待度数を求める方法は図2と同じ。セルB14に入力した「=(B4:C5-B9:C10)^2/B9:C10」によって、個々の「(実測度数−期待度数)2/期待度数」の値が求められる。それらを全て合計して求めたχ2値がセルD16の値。セルD18のCHIDSQ.DIST.RT関数で右側確率を求める。
セルB14〜C15で、実測度数と期待度数の差の二乗を期待度数で割った値を求め、それらを合計してセルD16でχ2値を求めています。ここでは計算の過程が分かるように、セルB14〜C15の値を求めて合計しましたが、スピル機能に慣れていれば=SUM((B4:C5-B9:C10)^2/B9:C10)と入力するだけで、χ2値が求められます([独立性の検定 (定義通りに計算・作成例)]ワークシートにその式で計算した例も含めてあります。もちろん、セルD16の値と一致します)。
独立性の検定での適切なサンプルサイズは?
最後に、適切なサンプルサイズの求め方を見ておきます。ここでは、理屈抜きに、標準正規分布を使って近似値を求めるための方法を示します。効果量wを求めるためには、まず、実測度数として想定される比率を指定します。例えば、関西人はうどんを好み、関東人はそばを好むと予想され、表1のような比率が想定されるものとしましょう。
| 関西 | 関東 | |
|---|---|---|
| うどん派 | 0.3 | 0.2 |
| そば派 | 0.2 | 0.3 |
実際に調査を行ってサンプルを採る前の段階では、人数は分からないので、比率で指定する。当然のことながら、全体の合計が1になるようにする。
効果量を求めるための以降の計算はχ2値を求める方法と全く同じです。効果量(cohen's w)をwと表すと、後で示す図4のセルD16の値がw2になります。有意水準をα、検出力を1−βとすると、以下の式でサンプルサイズが求められます。
独立性の検定は片側検定ですが、サンプルサイズを近似的に求める場合には両側確率を指定します(詳細な理由は割愛しますが、非心カイ二乗分布《平均が0からずれている特別なカイ二乗分布》を標準正規分布で近似する場合に両側確率が必要となるためです)。従って、上の式では、z1−α/2となっていることに注意してください。[サンプルサイズ (z近似)]ワークシートを開き、図4のように操作します。
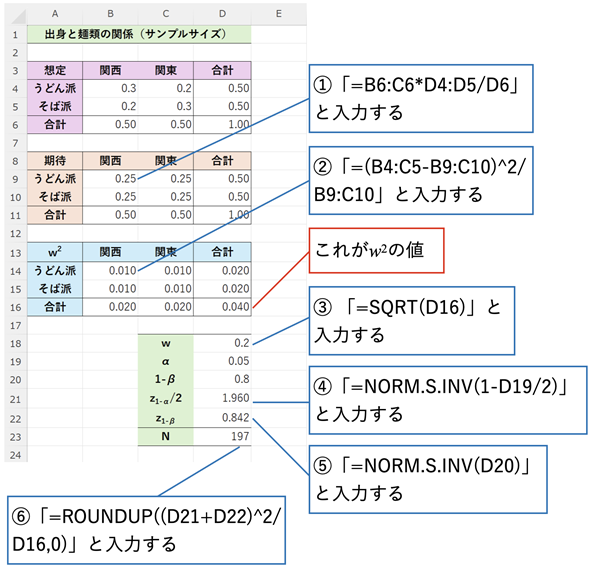
図4 独立性の検定(カイ二乗検定)のサンプルサイズを見積もる
手順は長いように見えるが、セルD16の値(w2)を求めるための計算は、図3で見たχ2値を求める計算と全く同じ。w2=0.040という値が求められた。後は(1)式に従って計算するだけ。なお、セルD18でwの値を求めているが、サンプルサイズの計算にこの値は使わない。
図4のセルB9〜C10では、想定される比率を基に期待値を求めていますが、あらかじめ母比率が分かっているのであれば、その比率を直接入力します。
(1)式による計算を手計算でも確かめておきます。α=0.05, 1−β=0.8とすると、z1−α/2=1.960,z1−β=0.842となります。w2=0.040なので、
となります。手計算では小数点以下を四捨五入した値を使っているので196となりますが、精度を上げるとExcelで計算した197という値になります。この197という値は個々のセルの度数ではなく、度数の合計を表します。
セルB4〜C5には比率を指定しますが、想定される度数を指定しても構いません(例えば、全体を仮にN=200として、関西のうどん派を60人と想定するなど)。その場合、セルD16で求めたχ2値をNで割っておけば、w2の値が求められます。
サンプルサイズの見積りをより正確に行うには、非心カイ二乗分布を利用する必要があります(分散の検定の場合にはカイ二乗分布を使いましたが、独立性の検定の場合には非心カイ二乗分布を使います。理由はかなり高度な話になるのでここでは割愛します)。検出力が1−β以上になるnの値を求めるPythonのプログラムをこちらに作成してあるので、興味のある方はご参照ください。最初のコードセルをクリックし、[Shift]+[Enter]キーを押してコードを実行するとn=197という結果が表示されます。
もっとも、実用的には前回紹介したG*Powerを使うのが簡単です。検定の方法などは以下のように指定します。
- Test family: χ2tests
- Statistical test: Goodness-of-fit tests: Contingency tables
- Type of power analysis: Compute required sample size - given α, power, and effect size
続けて、[Determine =>]ボタンをクリックし、右側に表示される画面で[Number of cells]に4を指定します。表の部分には、期待される比率を[p(H0)]の欄に、想定される比率を[p(H1)]の欄に入力します。Excelで作成したクロス集計表の形ではなく、対応する値を順に入力することに注意してください(図5)。
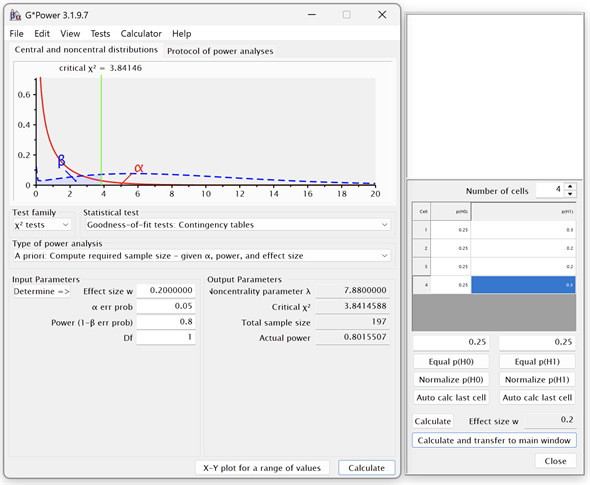
図5 G*Powerで独立性の検定(カイ二乗検定)のサンプルサイズを見積もる
上記の方法で検定の方法などを指定し、比率を入力した後、[Calculate and transfer to main window]ボタンをクリックすれば、[Effect size w]が自動的に計算されて表示される。α、1-β、自由度(Df)の値を入力し、[Calculate]ボタンをクリックすれば、[Total sample size]の欄に必要なサンプルサイズが表示される。
今回は、独立性の検定について、その考え方や方法を解説しました。実測度数と期待度数とがどの程度離れているかを基に、カイ二乗分布を利用して検定を行うということでした。カテゴリの分け方によっては、全体の比率と個々の項目の比率とに違いが生じるシンプソンのパラドックスについても少し触れました。
次回も項目同士の関係に焦点を当て、相関係数の検定(無相関の検定)に取り組みます。次回もお楽しみに!
この記事で取り上げた関数の形式
関数の利用例については、この記事の中で紹介している通りです。ここでは、連載で初出となる関数の基本的な機能と引数の指定方法だけを示しておきます。
独立性の検定(カイ二乗検定)を行うために使った関数
CHISQ.TEST関数: 独立性の検定を行う
形式
CHISQ.TEST(実測値の範囲, 期待値の範囲)
引数
- 実測値の範囲: 実測度数が入力されている範囲を指定する。
- 期待値の範囲: 期待度数が入力されている範囲を指定する。
Copyright© Digital Advantage Corp. All Rights Reserved.